机器学习
|
228
|
0
|
笔记

16304 字
|
1.1 小时
考试内容
考试形式：开卷，可带任何纸质资料
考试语言：中文
考试题型：判断、选择、简答、计算、系统设计
注意事项：带计算器

引言

定义：一种人工智能技术，可以让机器通过数据自动发现统计规律（模型），并不断优化自身性能（优化），以实现特定目标（如最小损失）

流程：数据准备（数据收集、特征提取）→ 训练（训练、验证）→ 评估（预测、评估）

机器学习分类

  • 监督学习
    • 数据：（x，y）其中x表示输入数据（特征），y表示标签（目标值）
    • 目标：学会映射函数 f(x) -> y ，即通过x预测y。映射函数可以为线性非线性or深度学习模型。
    • 典型任务：分类（如判断是否为垃圾邮箱，猫狗等），回归（预测股票），目标检测（识别特定目标，并用边界框标记位置），语义分割（对图像每一个像素都分类，如自动驾驶分割道路车辆行人标志各个区域）
  • 无监督学习
    • 数据：x
    • 目标：无监督学习通过分析数据的分布或结构，找出数据潜在的规律特点
    • 特点：聚类（把数据分组，类似数据分为一类），降维（PCA之类的，用来简化结构并尽可能保留特征），概率密度估计（风险评估），数据生成（从原始数据中学习分布并生成类似的新数据），异常检测（识别数据中异常的点or异常模式）
  • 强化学习
    • 数据：来源于和环境的交互，包括
      • 状态：智能体当前状态
      • 观察：智能体对环境的观察
      • 动作：智能体的行为选择
      • 奖励：执行某一个动作后的反馈，用来指导学习
    • 目标：把状态state映射到动作action，以最大化长期收益
    • 典型任务：策略优化，蒙特卡洛强化学习（模拟环境和智能体的交互来优化策略），值函数估计（股票长期收益），游戏AI（AlphaGo），机器人控制

泛化能力

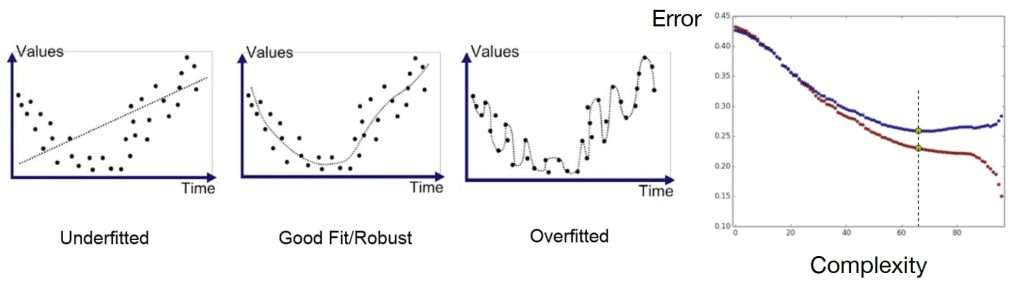
欠拟合：模型不够复杂，没办法刻画真实规律，模型假设不成立
过拟合：模型过于复杂导致记住的细节不是潜在规律（随机噪声之类）
欠拟合和过拟合本质：模型的复杂度，模型需要在二者之间平衡

避免方法：

  • 增加训练数据
    • 通过大量数据抑制模型记忆每个数据的细节
  • 正则化
    • 在损失函数中引入对模型参数的惩罚项，限制参数大小或稀疏性。原理可以通过对损失函数求梯度，参考文章
      • $ L(W, \lambda_1, \lambda_2) = ||y – WX||_2^2 + \lambda_2 ||W||_2^2 + \lambda_1 ||W||_1 $
        • L1正则化：惩罚模型参数的绝对值，使得部分参数趋于零（稀疏化），便于筛选出重要特征
        • L2正则化：惩罚模型参数的平方，使得参数值较小但不为零（平滑化），以此来降低噪声敏感度。
  • 数据划分&交叉验证
    • 通过将数据划分为训练集、验证集和测试集，确保模型不仅在训练数据上表现好，还在未知数据上表现好。
    • e.g. K折交叉验证：将数据分为K份，每次用其中一份作为验证集，其他K-1份作为训练集，循环K次。
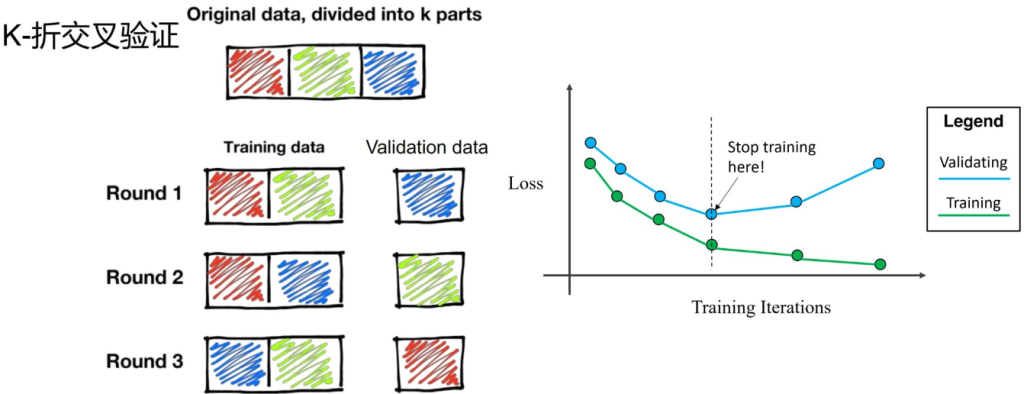
  • 早停：模型开始变差就停止训练
  • 引入先验知识（如贝叶斯先验）
    • 约束模型的学习过程，使其更符合实际问题的规律。
  • 设计好的损失函数

线性回归

回归问题

通过实验观测数据，揭示变量之间的统计关系，回归变量的真实值。

即：建立数学关系 y= f(X)+ϵ。其中X为自变量，y为因变量，f(X)为回归模型（拟合模型），ϵ为随机误差（无法被解释的部分）

线性回归

回归函数为线性表达式，即 y=f(X)=wTX+w0

  • X = [x1,x2,……,xd]：输入特征向量（自变量）。
  • W = [w1,w2,……,wd]：模型的参数（权重）。
  • w0：偏置项
  • f(X)：预测值

对于训练过程，是根据误差，不断调整参数wT和w0
对于预测过程，是对于新数据x，计算f(x)，得到回归值y

损失函数

单个样本的平方方差，其中x为输入样本，y为模型输出，真实值为r：

$$l(w, w_0 \mid x, r) = (r – y)^2$$

对于整个数据集D={(x(1),r(1)),…,(x(n),r(n))}（N个样本）的均方误差（MSE）定义为：

$$L(w, w_0 \mid D) = \frac{1}{2N} \sum_{i=1}^N (r^{(i)} – \hat{y}^{(i)})^2$$

除以2是为了简化后续梯度公式推导，常数系数不会影响模型优化方向。

优化

优化的目标为最小化损失函数： $ \min_w L(w) $
迭代步骤：$ w_{t+1} = w_t – \eta_t \frac{\partial L}{\partial w} $

计算$ \frac{\partial L}{\partial w} $:
对于任意参数wj：$ \frac{\partial L}{\partial w_j} = -\frac{1}{N} \sum_{i=1}^N (r^{(i)} – \hat{y}^{(i)}) \frac{\partial L^{(i)}}{\partial w_j} = -\frac{1}{N} \sum_{i=1}^N (r^{(i)} – \hat{y}^{(i)}) x_j^{(i)} $

迭代规则：$ w_{\text{new}} = w_{\text{old}} – \frac{1}{N} \sum_{i=1}^N (r^{(i)} – \hat{y}^{(i)}) x_j^{(i)} $

矩阵形式

对于梯度下降法求线性回归其实没必要，因为通过数学可以直接得到最优值。

令：

$$
X =
\begin{bmatrix}
x^{(1)} \\
x^{(2)} \\
\vdots \\
x^{(N)}
\end{bmatrix} =
\begin{bmatrix}
x_0^{(1)} & x_1^{(1)} & x_2^{(1)} & \dots & x_d^{(1)} \\
x_0^{(2)} & x_1^{(2)} & x_2^{(2)} & \dots & x_d^{(2)} \\
\vdots & \vdots & \ddots & \ddots & \vdots \\
x_0^{(N)} & x_1^{(N)} & x_2^{(N)} & \dots & x_d^{(N)}
\end{bmatrix},
\quad
w =
\begin{bmatrix}
w_1 \\
w_2 \\
\vdots \\
w_d
\end{bmatrix},
\quad
r =
\begin{bmatrix}
r^{(1)} \\
r^{(2)} \\
\vdots \\
r^{(N)}
\end{bmatrix}
$$

那么此时，预测值：$ y = Xw =
\begin{bmatrix}
x^{(1)} w \\
x^{(2)} w \\
\vdots \\
x^{(N)} w
\end{bmatrix} $
损失函数：$ L(w) = \frac{1}{2} (r – y)^T (r – y) = \frac{1}{2} (r – Xw)^T (r – Xw) $
梯度： $ L(w) = \frac{1}{2} (r – y)^T (r – y) = \frac{1}{2} (r – Xw)^T (r – Xw) $
令梯度为0，得到：$ \frac{\partial L(w)}{\partial w} = 0 \implies X^T (r – Xw) = 0 \implies X^T r = X^T X w $
从而得到：$ w^* = (X^T X)^{-1} X^T r $
带入$ w^* $，最后得到预测值 $ y = X (X^T X)^{-1} X^T r = H r $
我们此时只需要算出H即可

问题：XTX可能不可逆（如x2=3x1），导致我们还是只能使用梯度下降法
解决：使用正则化，对损失函数引入惩罚项

新的损失函数：$ L(w) = \frac{1}{2} (r – y)^T (r – y) = \frac{1}{2} (r – Xw)^T (r – Xw) + \frac{\lambda}{2} |w|_2^2 $
新的梯度：$ \frac{\partial L(w)}{\partial w} = -X^T (r – Xw) + \lambda w $
新的最优解：$ \frac{\partial L(w)}{\partial w} = 0 \implies -X^T (r – Xw) + \lambda w = 0 \implies X^T r = (X^T X + \lambda I) w $
从而得到：$ w^* = (X^T X + \lambda I)^{-1} X^T r $
因为XTX + λI一定是满秩的，所以一定可逆

决策树

  • 回归（预测连续值标签）：
    • 对数据点在（d+1）维空间（d 是特征维度，+1 维是标签轴 y）中的分布进行建模。
  • 分类（预测类别标签）：
    • 对 d 维空间中不同类别数据的分界边界进行建模，通过决策边界划分不同类别区域。

分类问题中，可能遇到无法线性分割的问题，或者属性非数字，但是沿着某些维度局部线性可分
解决思想：分而治之（创建一系列if then条件），通过决策树建立一系列决策规则对数据进行分类。

构造决策树的过程：

  • 构造一个根节点，包含整个数据集
  • 选择一个最合适的属性
  • 根据选择属性的不同取值，将当前节点的样本划分成若干子集
  • 对每个划分后的子集创建一个孩子节点，并将子集的数据传给该孩子节点
  • 递归重复2~4直到满足停止条件

如何高效构建决策树？
选择每个属性X的时候，尽可能最大化标签Y的纯度。

如何选择属性以最大化标签的纯度？
选择X以最大化信息增益、Gini系数等

ID3算法

根据信息增益进行划分，目标是使信息增益（Information Gain）最大化

信息熵表示数据集合的不纯净度，公式：

$$H(D) = -\sum_{k=1}^{K} p_k \log p_k = -\sum_{k=1}^{K} \frac{|C_k|}{|D|} \log \frac{|C_k|}{|D|}$$

$ |C_k| $：数据集中属于类别$ C_k $的样本数量
$ |D| $：数据集的总样本数量

条件熵表示数据集在某个属性 A 条件下的不纯净度，公式：

$$H(D|A) = \sum_{i=1}^{n} \frac{|D_i|}{|D|} H(D_i) = -\sum_{i=1}^{n} \frac{|D_i|}{|D|} \left( \sum_{k=1}^{K} \frac{|D_{ik}|}{|D_i|} \log \frac{|D_{ik}|}{|D_i|} \right)$$

$ |D_i| $：数据集中属性 A 取第 i 个值的样本数量；
$ |D_{ik}| $：在 Di 中属于类别 Ck 的样本数量。

信息增益表示选择某个属性 A 后，信息熵的减少程度：

$$Gain(D, A) = H(D) – H(D|A)$$

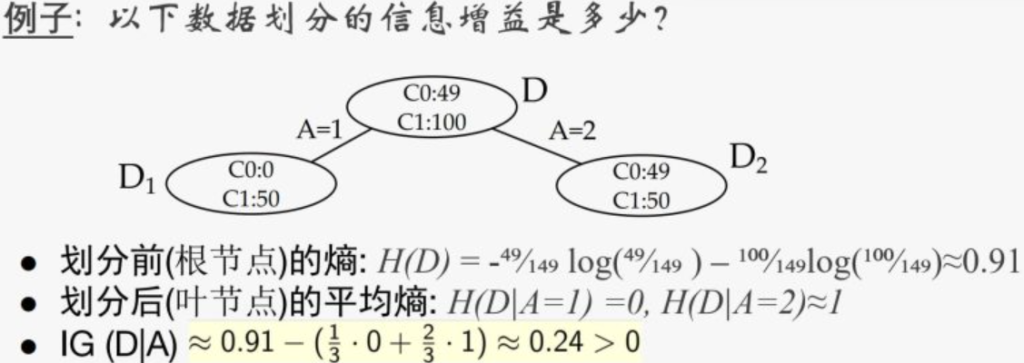
例题

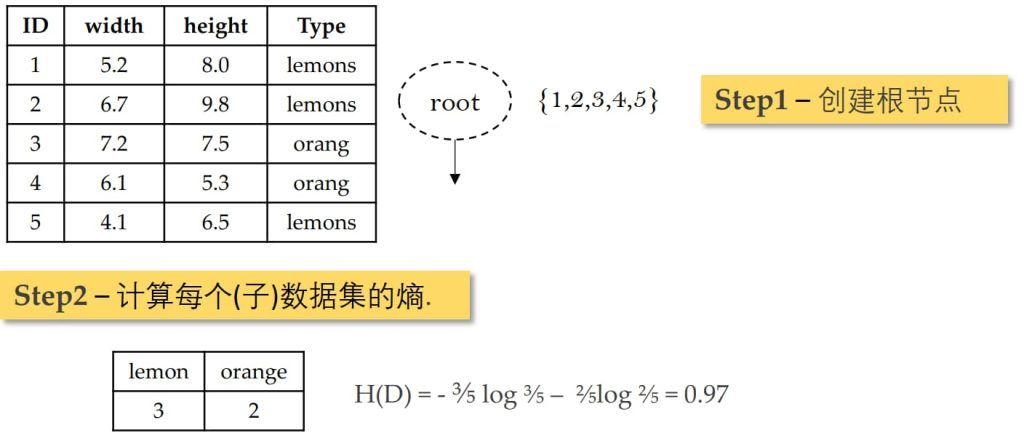
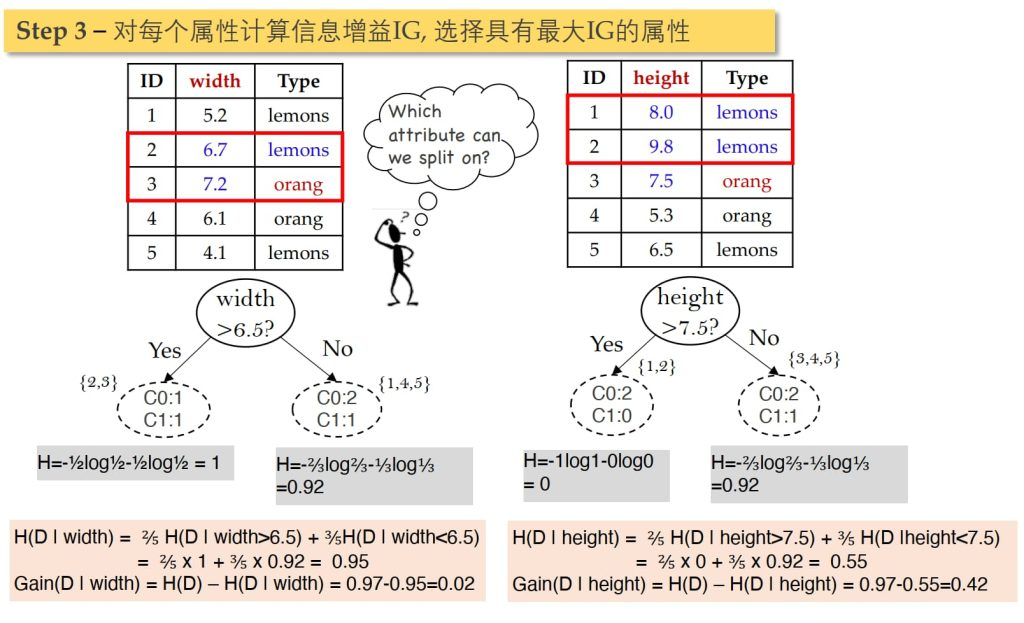
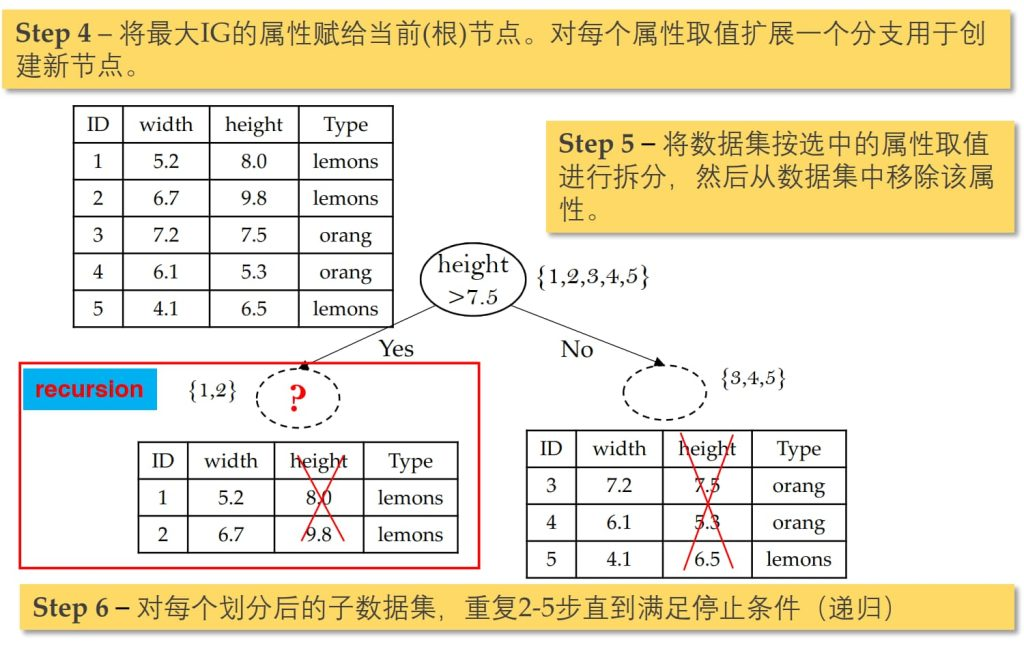
停止划分条件：

  • 纯度：叶子节点包含的样本均属于同一类
  • 数据量过小：叶子节点包含的样本数小于一个阈值
  • 没有属性可分（ID3）：ID3对每个属性只划分一次

优点：简单，便于可视化分析；对数据预处理要求低，可以容易处理非线性边界，数据驱动，可以任意拟合数据集
缺点：过拟合（噪声样例也会被学习）

解决：随机森林

将数据随机划分子集，各自构建决策树，按多个决策树的结果投票决定。

  • 优点（用随机性换稳定性，用集成换精度）：
    • 通过双重随机性（数据自助采样 + 特征子集随机选择）降低过拟合风险，比单棵决策树更准确；
    • 可以处理高维数据，并且不用做特征选择 (因为特征子集是随机选择的)；
    • 训练速度快（树与树独立生成，天然支持并行化）；
    • 可处理缺失值、不平衡数据（通过采样平衡误差）和特征交互（自动检测特征间关系）；
    • 提供特征重要性排序，同时保持集成模型的直观解释性（i.e.,在训练完后，能够给出哪些feature比较重要）。

贝叶斯分类

对于数据交融在一起，决策树没有办法精准区分

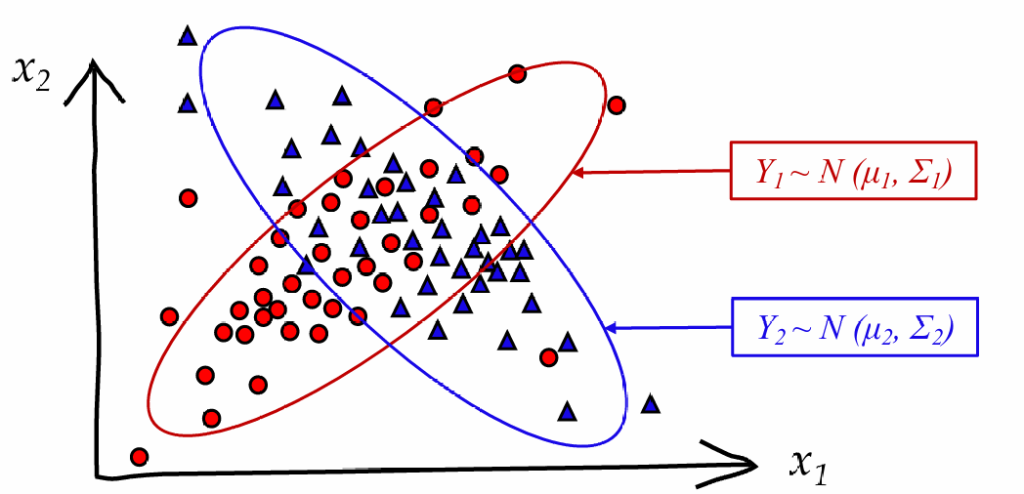
解决：依靠概率论，通过计算某个点属于某一类的概率解决问题。

贝叶斯公式：$ P(C_i|x)=\frac{p(x|C_i)P(C_i)}{p(x)}, \ i=1,2,\dots,N $

  • Ci 是第 i 个类别（共N个），x 数据特征向量；
  • P(Ci) 先验概率，在未观测数据时，类别 P(Ci) 的初始概率（可通过训练集频率估计）；
  • p(x|Ci) 似然概率，在类别 Ci 成立的条件下，观测到数据 x 的概率；
  • p(x) 证据概率，是所有类别下生成特征 x 的总概率，用于归一化；
  • p(x)=∑Ni=1P(Ci)p(x|Ci)
  • p(Ci|x) 后验概率，观察到数据 x 后，样本属于类别Ci的概率。

对于多个特征，公式变为：

$$ P(C_i | x_1, x_2, \dots, x_d) = \frac{p(x_1, x_2, \dots, x_d | C_i) P(C_i)}{p(x_1, x_2, \dots, x_d)} $$

由于我们只考虑概率的相对大小，因此只用计算分子的部分：

$$ P(C_i | x_1, x_2, \dots, x_d) \propto p(x_1, x_2, \dots, x_d | C_i) P(C_i) $$

独立性假设（朴素贝叶斯假设）

如果各个特征之间xj都是独立的，则：

$ p(x_1,x_2,\dots,x_d|C) = P(x_1|C) \cdot P(x_2|x_1,C) \dots P(x_d|x_1,\dots,x_{d-1},C)$
$ \approx P(x_1|C) \cdot P(x_2|C) \dots P(x_d|C) $

此时，贝叶斯公式可以简化为

$$ P(C_i | x_1, x_2, \dots, x_d) \propto P(C_i) \prod_{j=1}^d p(x_j | C_i) $$

虚拟计数修正

计算 𝑃(𝑥𝑗∣𝐶𝑖) 时，可能出现某些值为 0 的情况，可以通过虚拟计数（平滑处理）修正：

$$ P(x_j | C_i) = \frac{\text{count}(x_j, C_i) + \alpha}{\text{count}(C_i) + \alpha \cdot |\text{X}|} $$

  • α 是平滑参数（如拉普拉斯平滑中 α=1）。
  • ∣X∣是所有特征取值的数量。

总结优缺点

  • 优点：
    • 训练和测试速度快。
    • 表现好：
      • 当独立性假设成立时，效果非常好。
      • 在多分类问题中表现良好。
    • 易于在数据集更新时进行训练，算法易维护。
  • 缺点：
    • 依赖于独立性假设，如果特征之间存在较强的相关性，模型效果可能受影响。
    • 容易欠拟合：由于模型的简单性，可能无法捕捉数据的复杂模式。

K-近邻 KNN

基本原则：根据距离自己最近的几个点的所属类别进行投票

选取指标

  • 距离指标
    • 欧氏距离：L2泛数，平方距离$ D(x,y) = \sqrt{\sum_{i=1}^n(x_i-y_i)^2} $
    • 曼哈顿距离：L1泛数$ D(x,y) = \sqrt{\sum_{i=1}^n|x_i-y_i|} $
    • 闵式距离：$ D(x,y) = \big( {\sum_{i=1}^n(x_i-y_i)^p} \big) ^\frac{1}{p} $
  • 归一化：保证各个属性尺度一致，便于处理
    • Z-score标准化：$ x_{\text{norm}} = \frac{x – \mu}{\sigma} $，把特征缩放到距离为0，标准差为1的分布
    • Min-Max归一化：$ x_{\text{norm}} = \frac{x – x_{\text{min}}}{x_{\text{max}} – x_{\text{min}}} $，把特征缩放到 [0, 1] 或 [-1, 1] 区间。
  • 相似度：不一定要用距离作为限制，用相似度也可以
    • 余弦相似度

算法过程

  • 预处理数据（特征标签归一化）
  • 计算输入样本与训练样本之间的距离（或相似度）
  • 对距离排序并选取 K 个最近邻样本
  • 根据 K 个邻居的多数投票结果确定测试样本类别

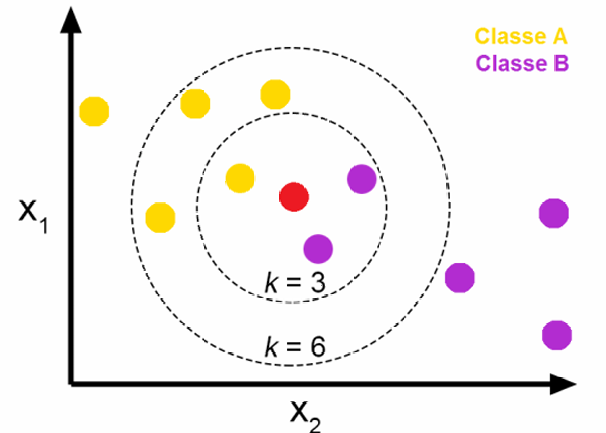
K值选取

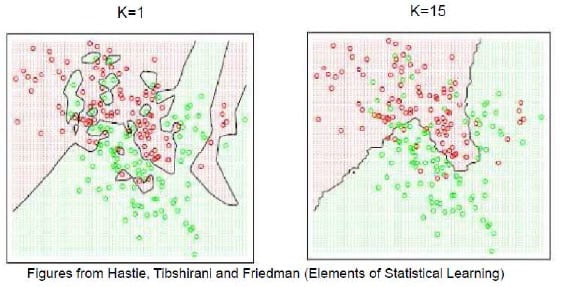
上面是维诺图，是把空间划分给定点最近的区域；边界表示二者相当，可以清楚看到K值影响

K值过小：更能反映局部细节，但会导致过拟合，容易被噪声影响
K值较大：边界更加平滑，也可能导致欠拟合，容易忽视细节

优缺点

  • 优点：
    • 易于理解、解释和实现，训练难度低
    • 可以无缝添加新数据，而不会影响模型的准确性
  • 缺点：
    • 不适用于大型数据集（计算距离的计算成本很高）
    • 极易受到维度的影响（高维数据失效）
    • 需要大量存储，需要数据归一化

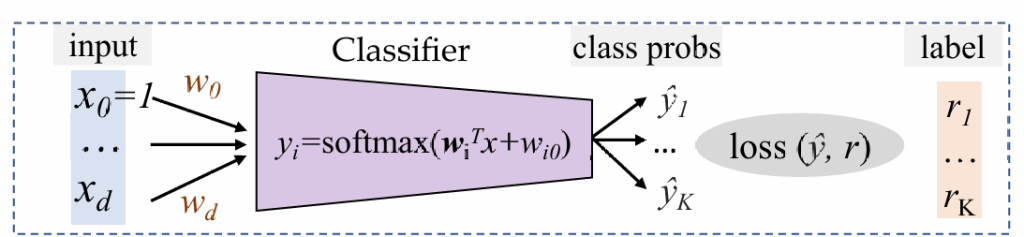
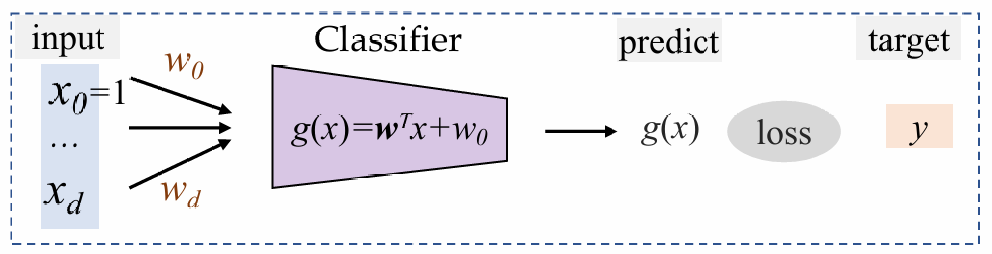
逻辑回归LR

利用判别函数，根据正负来决定分类。此时，逻辑回归学习这个判决函数直接建模决策边界，而不需要估计数据的概率分布。

优势：通常效率比较高

感知机

结构非常简单，朴素分类（只有-1和1）

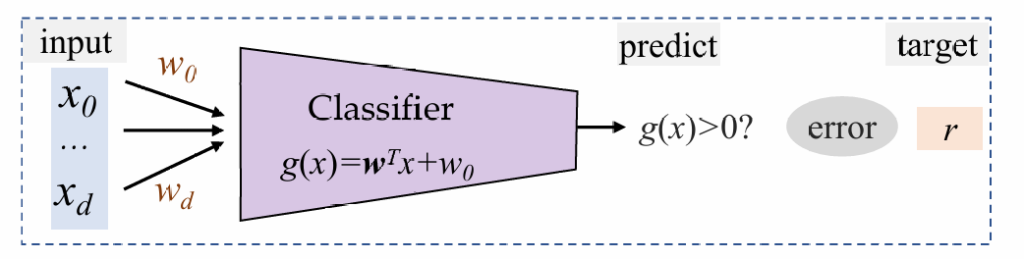
训练过程：

规定数据集D={(x(1),r(1)),...,x(d)r(d)};
for (x(l),r(l)) in D:（对于每一个数据和标签）
| if r(l)g(x(l))≤0:（预测与实际不一致）
| | w=w+ηr(l)x(l)（将超平面向被错误分类的点移动，η为学习率）
重复上述过程，直至全部数据集都被正确分类

感知机限制：取值只有-1和1，对于优化来说非常困难

sigmoid

定义y为数据点x属于类别C1的概率，那么对应C2概率就是1-y
此时，根据$ \log \frac{y}{1 – y} $判断，应该属于哪一类，然后推导得到：

$ \log \frac{y}{1 – y} = \mathbf{w}^T\mathbf{x} + w_0 \Rightarrow y = \text{sigmoid}(\mathbf{w}^T\mathbf{x} + w_0) = \frac{1}{1 + \exp [-(\mathbf{w}^T\mathbf{x} + w_0)]} $

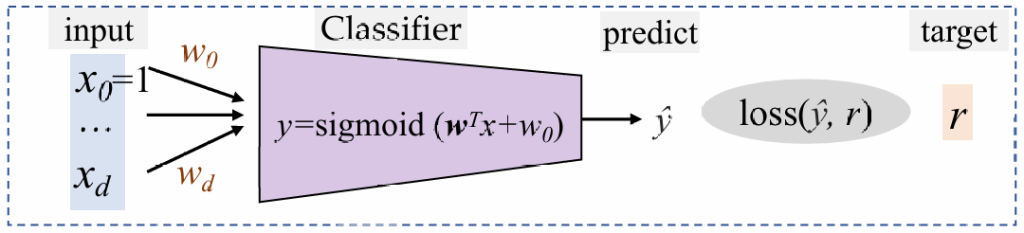
训练：从数据中预测参数 w,w0 。
预测：给定一个新 x，计算$ y = \text{sigmoid}(\mathbf{w}^T \mathbf{x} + w_0) $，选择$ C_1 \ \text{if} \ y > 0.5 \ \text{otherwise} \ C_2 $（y也可以认为是后验概率）

损失函数：因为是二分问题，所以最后对于r为0或1，则对应过来

  • 如果 r=1，最大化 logP(C1​∣x)=logy（损失为-logy ）。
  • 如果 r=0，最大化 logP(C2​∣x)=log(1−y)（损失为-log(1-y) ）。

为了把二者统一起来，定义一个新损失函数，即交叉熵损失CE：

$ \ell(w, w_0 | x, r) = -r \log y – (1 – r) \log (1 – y) $

最小化损失函数等价于最大化似然

$ p(r \mid x) = y^r(1-y)^{(1-r)}=\begin{cases} y \quad \text{if} \ r = 1 \\ 1-y \quad \text{if} \ r = 0 \end{cases} $

训练过程

通过梯度下降法最小化损失函数 $ w_{t+1} = w_t – \eta \frac{\partial L}{\partial w} $

对于整个数据集 D 而言：$ L(w, w_0 \mid D) = -\sum_{l=1}^N \left( r^{(l)} \log y^{(l)} + (1 – r^{(l)}) \log(1 – y^{(l)}) \right) $

我们定义：$ a = w^T x + w_0 $

那么带入到上面的公式，可以得到$ y = \text{sigmoid}(a) $，$ \frac{\partial a}{\partial w_j} = x_j^{(l)} $和$ \frac{\partial y}{\partial a} = y(1 – y) $

最后可以得到：

$ \frac{\partial L}{\partial w_j} = -\sum_{l=1}^N \left( \frac{\partial L}{\partial y^{(l)}} \cdot \frac{\partial y^{(l)}}{\partial a^{(l)}} \cdot \frac{\partial a^{(l)}}{\partial w_j} \right) = -\sum_l \Big( r^{(l)} – y^{(l)} \Big) x_j^{(l)} $

其中r(l)是真实标签，y(l)是预测值，xj表示特征值

多分类问题

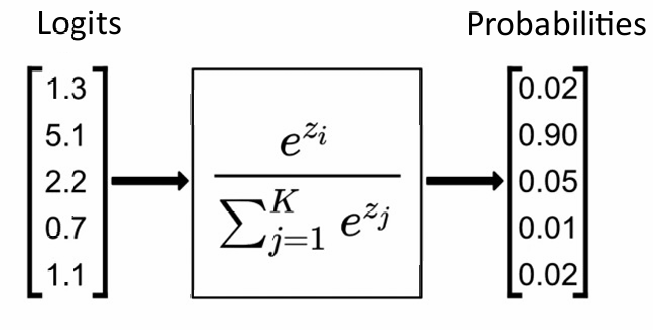
有时我们需要预测多个类，如果我们想统一处理所有类而不必选择参考类，我们可以使用 softmax 函数来代替后验类概率y

$ y_i = \text{softmax}(a_1, \dots, a_K)i = \frac{e^{a_i}}{\sum{j=1}^K e^{a_j}} $

其中 $ a_i = W_i x + w_{i0} $，被称为logits，Wi，wi0为可训练参数

交叉熵损失函数及梯度：

$ L_{CE}(y, r) = -\sum_{i=1}^{k} r_i \log y_i = -r^T (\log y) $
$ \frac{\partial L}{\partial w_j} = -\sum_l \Big(r_j^{(l)} – y_j^{(l)}\Big) x_j^{(l)} $

支持向量SVM

对于之前的分裂方法，目标只是一个正确的结果。当然这个结果也可以更进一步优化，追求效果应该是最大化两个边界距离的决策边界

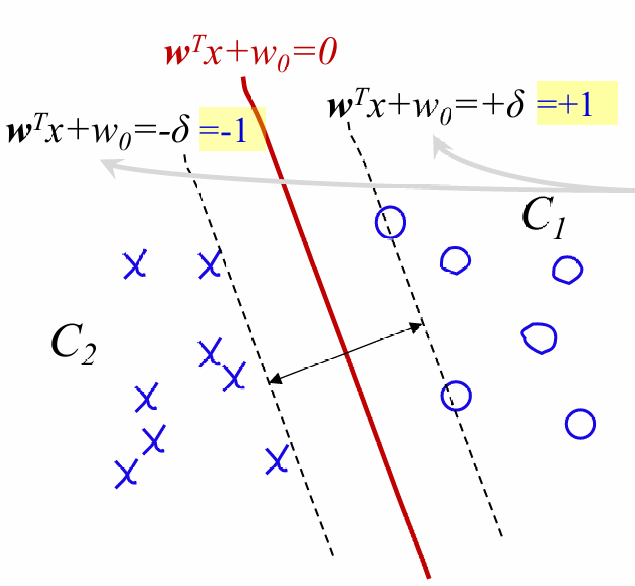
上式相减，最后得到间距：

$ margin = \frac{2}{||w||} $

最大化margin则等价于最小化 $ 0.5 ||w|| $

那么写出一个最优化问题的形式：
minimize $ \frac{1}{2} |\mathbf{w}|^2 $
subject to $ y^{(\ell)} (\mathbf{w}^T x^{(\ell)} + w_0) \ge 1, \ell=1,\dots,N $

因为y的取值只有±1，所以保证了所有点在两条虚线外，采用感知机作为模型

对于这个，我们首先希望y(wTx+w0)>1，所以需要优化其中最小的值，直至其大于1
当所有点都在虚线外，我们开始调整w使其最终卡在边界上

多层感知机制

模仿了人类大脑的某些特性，根据人类的神经结构，科学家构建出人工神经网络ANN。

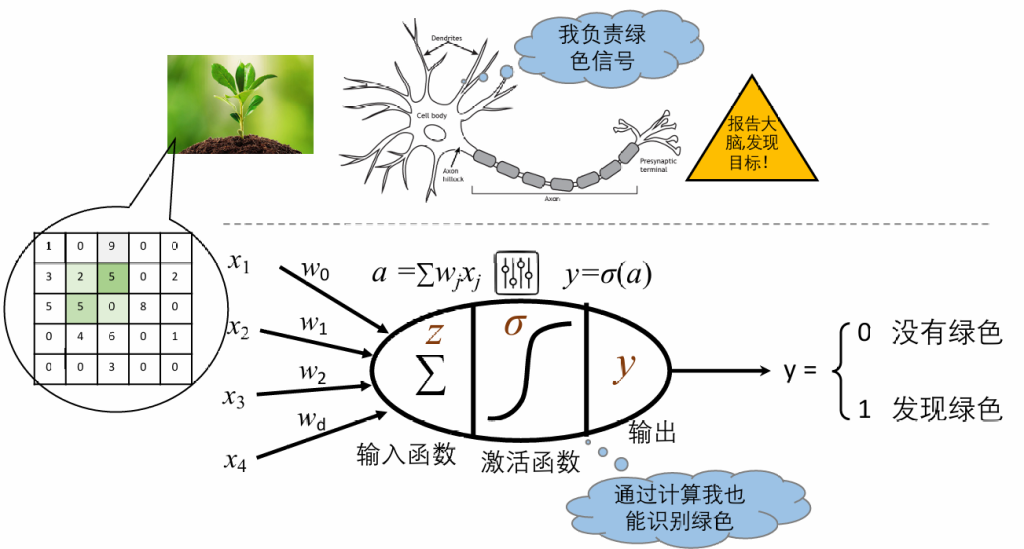
如果其中的激活函数σ ()是sign()符号函数的话，这个神经元就是之前学过的感知机。
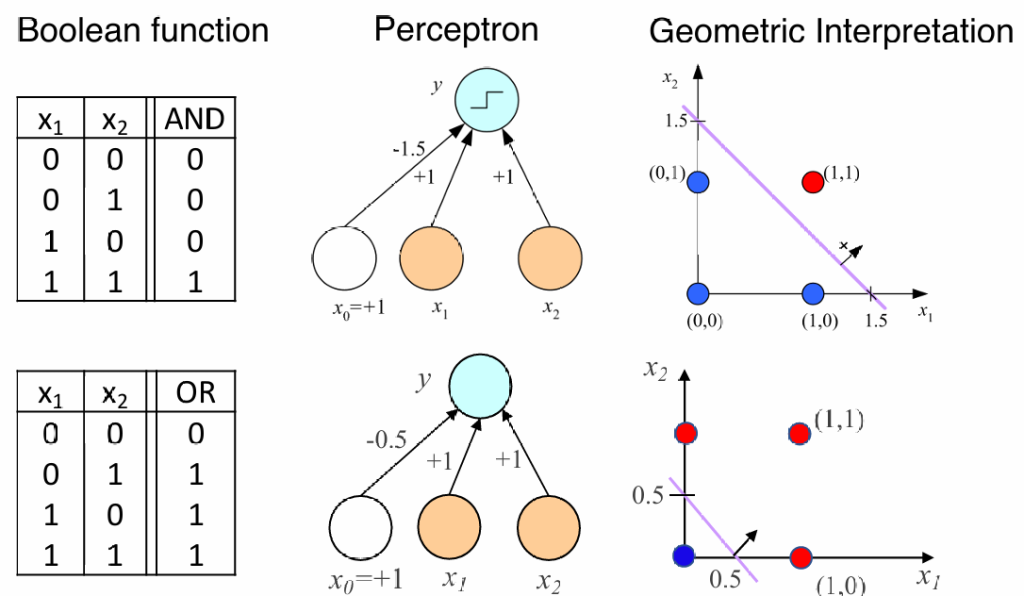
我们可以通过感知机来模拟与或运算：

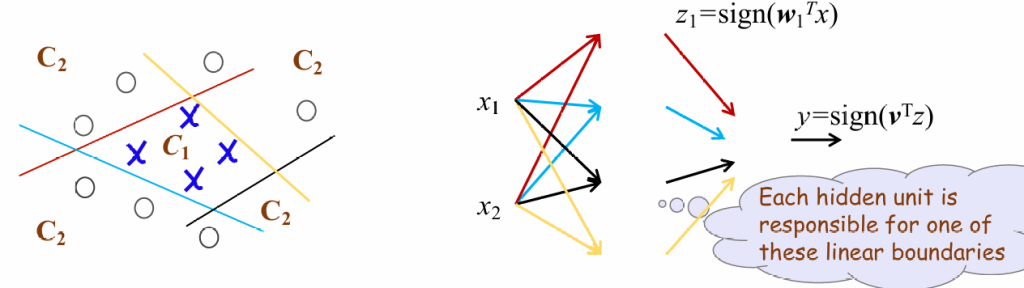
如果继续添加隐藏层，就可以模拟一些非线性操作，比如说XOR

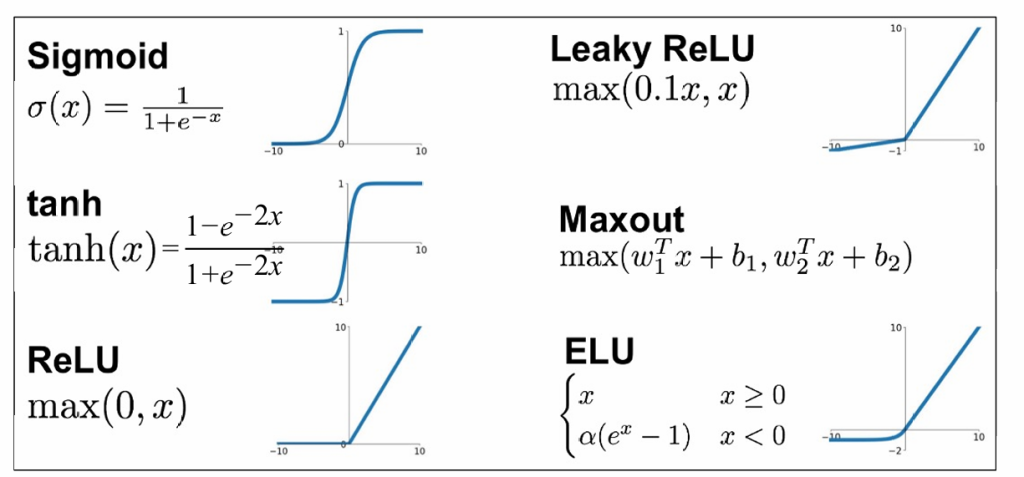
还有很多其它的激活函数，这些都为非线性

也可以构建多层感知机结构，实现连续的（可微分的）决策

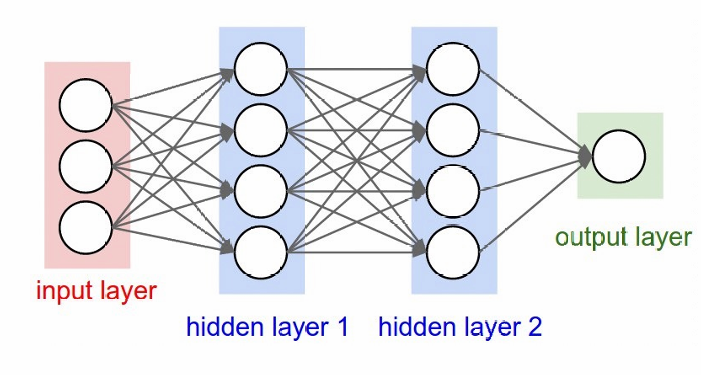
训练的核心就在于算梯度：通过误差找局部极小值点，让 θ 朝着梯度的反方向移动步长（梯度下降法）。

可以得到损失函数，m是输出的值的维度。我们需要最小化均方误差（MSE）损失： $ \mathcal{L}(\theta \mid D) = \frac{1}{2} \sum_{\ell=1}^N \sum_{i=1}^m \left( r_i^{(\ell)} – y_i^{(\ell)} \right)^2 $

对于单个样本（x，r）误差：$ \ell(x, r) = \frac{1}{2} \sum_{i=1}^m \left( r_i – y_i \right)^2 $

由于直接计算过于复杂，因此我们需要使用反向传播计算梯度

误差反向传播过程：

  • 前向传播：
    • 在前向传播过程中，输入数据从输入层经过隐藏层传递到输出层，计算出模型的预测值 ypred和损失值 L。
  • 反向传播：
    • 根据链式法则（用于处理复合函数求导的重要规则），计算损失函数相对于每个参数的梯度 ∂L/∂w，从输出层向输入层逐层反向传播。
  • 参数更新：
    • 利用梯度下降等优化算法，通过梯度信息更新每层的权重和偏置：w=w−η⋅∂w/∂L，其中w为参数，η为学习率

反向传播过程：

我们需要计算所有的

\frac{\partial L}{\partial w_{i,j}^k} \quad i \in {1,2,\cdots,n}; j\in {1,2,\cdots,n}; k\in {1,2,\cdots\,L+1}

我们先关心输出层，我们需要计算所有的

\frac{\partial L}{\partial w_{i,1}^{L+1}} \quad i \in {1,2,\cdots,n}

容易得到

\frac{\partial L}{\partial w_{i,1}^{L+1}}=\frac{\partial L}{\partial a_{1}^{L+2}}\frac{\partial a_{1}^{L+2}}{\partial w_{i,1}^{L+1}}=\frac{\partial L}{\partial a_{1}^{L+2}}x_{1}^{L+1}

我们再考虑位于L层的第j个神经元
我们需要计算所有的

\frac{\partial x_{j}^{L}}{\partial w_{i,j}^{L-1}} \quad i\in {1,2,\cdots,n}

可以得到

\frac{\partial x_{j}^{L}}{\partial w_{i,j}^{L-1}}=\frac{\partial x_{j}^{L}}{\partial a_{j}^{L}}\frac{\partial a_{j}^{L}}{\partial w_{i,j}^{L-1}}=\frac{\partial x_{j}^{L}}{\partial a_{j}^{L}}x_{i}^{L-1}

现在，如果能计算出∂L/∂x，那么我们就能计算出我们想得到的所有数据。

我们考虑输出层神经元
我们需要计算：

\frac{\partial L}{\partial x_{i}^{L+1}} \quad i \in {1,2,\cdots,n}

注意到

\frac{\partial L}{\partial x_{i}^{L+1}}=\frac{\partial L}{\partial a_{1}^{L+2}}\frac{\partial a_{1}^{L+2}}{\partial x_{i}^{L+1}}=\frac{\partial L}{\partial a_{1}^{L+2}}w_{i,1}^{L+1}

注意，如果是中间层，则最后是求和的形式，因为x被使用n次

上面的推导非常复杂，但我们只需要知道：

\frac{\partial L}{\partial w_{i,j}^{L}}=\frac{\partial a_{j}^{L}}{\partial w_{i,j}^{L}} \frac{\partial L}{\partial a_{j}^{L}}

我们将第一部分称为输入，后一部分称为误差；输入是wi,jL上对应的xiL，而误差δjL可以根据下面的式子递归计算

\delta^{L}=\sigma'(x^L)\cdot (r-y)\\\delta^{L-1}=\sigma'(x^{L-1})\cdot (W^L)^T \delta^L \\\cdots

递归计算梯度的时候会经常重复，可以使用动态规划优化

深度学习的特点：

  • 自动学习数据表征
  • 学习层次化表征
  • 端到端学习

题目：

σ这里是SIgmoid函数，即激活函数

语言模型

Word2vec

单纯使用ASCII码，机器无法理解数字的意义，无法理解单词与单词间的关系
one-hot编码：每个单词占有向量中的一位，这一位为1，其余为0；非常占用空间，并且不能反映词间关系
我们希望使用一种压缩的向量，并且能够反映词间关系

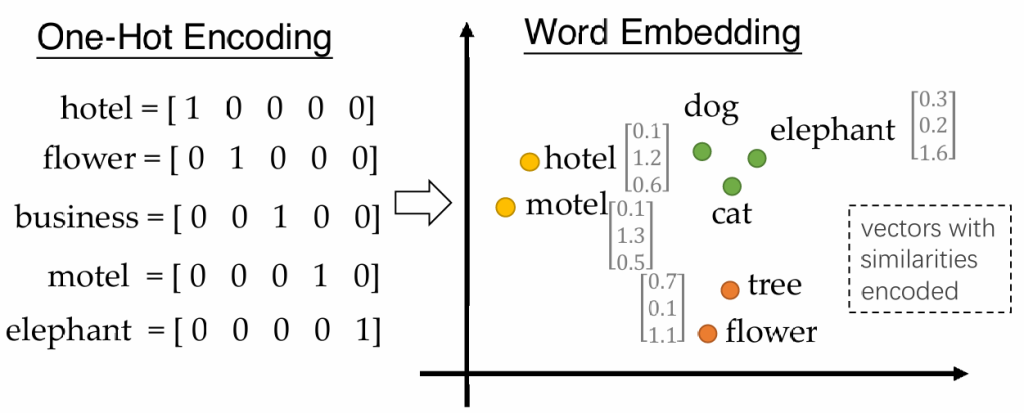
如何获取单词编码呢？基本想法，如果未知单词和已知单词有相似的上下文，则认为二者相似，对应算法：

  • 准备一个大规模的文本库
  • 给每个单词分配一个词向量
  • 遍历文本，获取单词w及其两边的词c
  • 根据向量相似度计算给定c后中间为w的概率
  • 更新词向量，直至概率最大化

此时得到了词向量，如果让计算机输出语句？
如果一句话由w1,..,wn构成，那么最后的概率p(x)=p(w1,w2,…,wn)如何计算？

基于条件概率，可以得到p(w1,w2,…,wn)=p(w1)p(w2|w1)…p(wn|w1,w2…)，而单词一般只和相近的单词有关，因此我们可以化简成只考虑前k个单词

那么我们如何获得这个条件概率？
最简单的想法是计数。缺点：依赖离散符号表示，面临数据稀疏问题（Data Sparsity）；实际没有学习到语义；对相关词和句子不敏感，对前缀变化极其敏感。

因此我们使用词向量代替单词。词向量可以反映相似度，但是这种方式还不能反映词与词间的顺序，所以我们将多个词向量进行拼接。这种方式的问题是输入的长度不可变，并且标点符号等会对其产生很大影响。

我们的要求：

  • 处理变长序列
  • 跟踪长期依赖关系
  • 保存有关顺序的信息
  • 在语句间共享参数

循环神经网络RNN

对于标准神经网络来说，一次只能处理一个单词。
设想是否可以让神经网络记录处理过的单词：为隐藏层添加回路以实现记忆能力。
核心思想：通过递归关系将当前时间步的输入与上一时间步的隐藏状态结合，更新隐藏状态，从而逐步处理序列数据并捕获时间序列中的上下文和依赖关系。

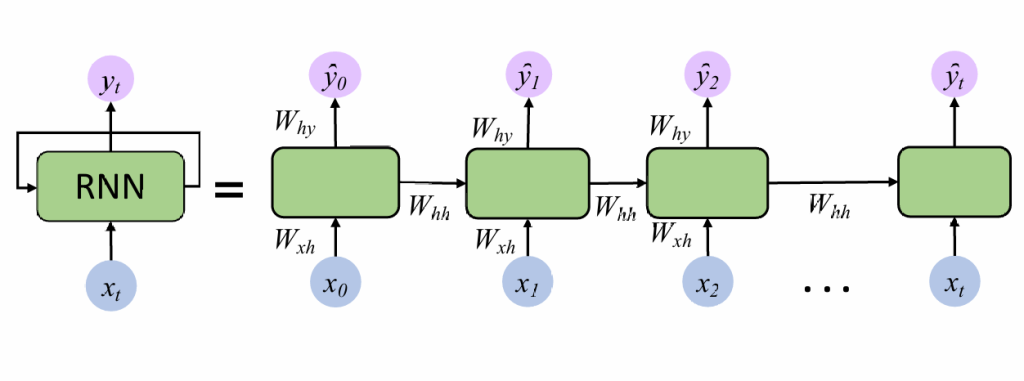
训练方法：通过时间的反向传播

应用：

  • 语句分类：分析一个单词序列的情感（Many-to-One）
  • 文本生成：预测生成文本
  • 机器翻译：使用编码器-解码器架构处理条件序列生成任务。（Many-to-Many）

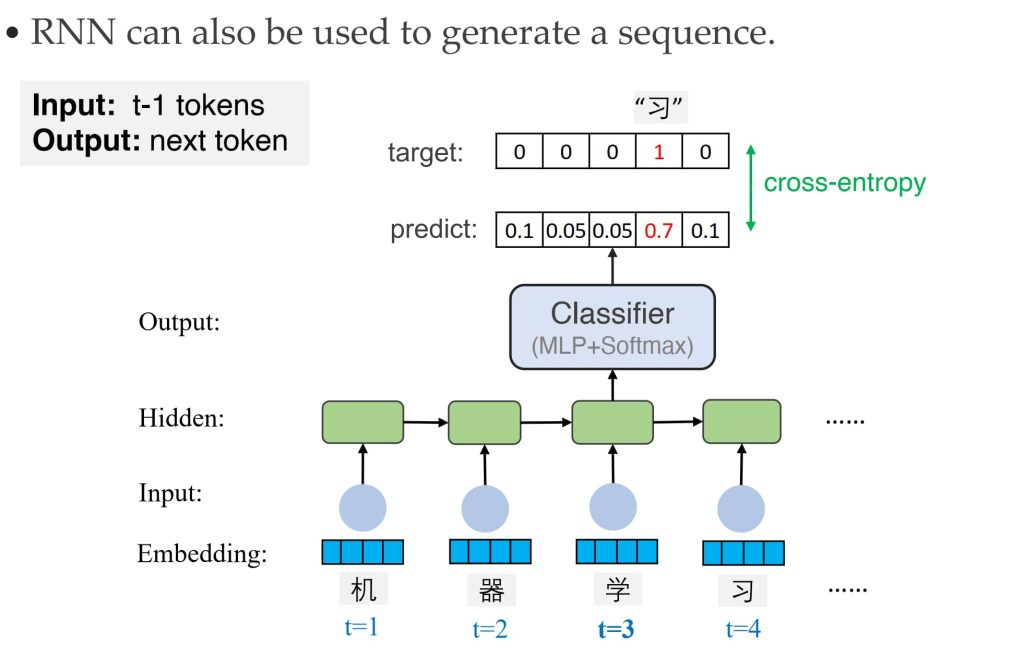
缺点：时间步之间存在依赖，因此无法并行化处理。同时对于较长时间的远程依赖关系表现不好。

Transformer

RNN的编解码器

使用两个RNN，一个作为编码器，处理输入序列，一个作为解码器，生成输出序列。通过这个通用的模型，我们可以完成语音转文字、翻译等工作

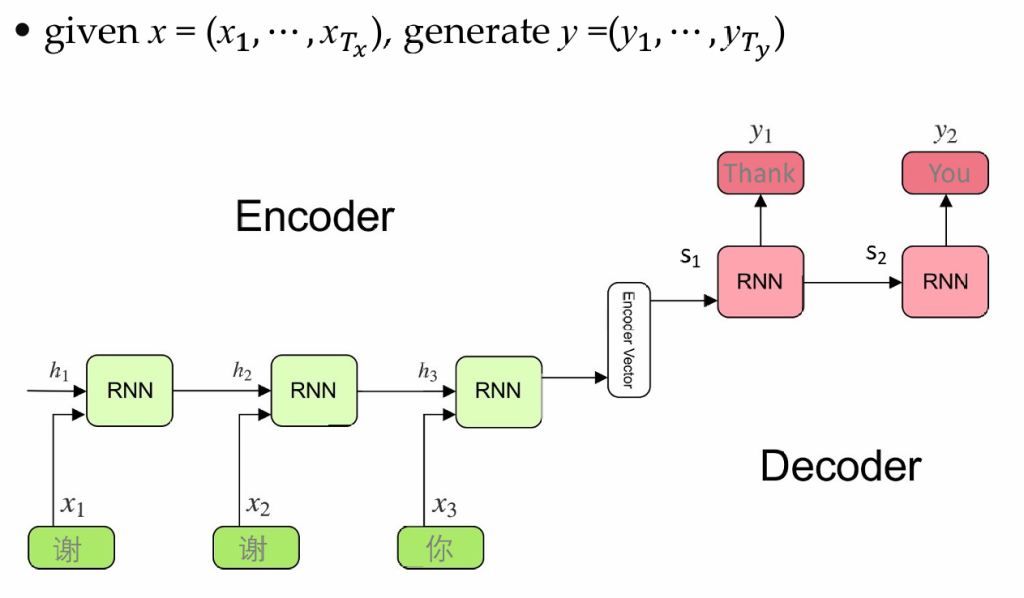
编码器吧输入的序列压缩成为一个向量c，解码器的任务是基于向量c生成序列，并通过分类器把生成的序列转化为自然语言。

训练过程：通过生成的y和真实值做比对，通过梯度下降最小化交叉熵损失函数

用途：除了文本生成、翻译等功能，还可以用于图像生成等。

缺点：无法理解长文本，因为向量c的表达能力是有限的，会带来很大的信息损失。所有信息都被等同对待，对于重要信息关注不够。
改进：动态编码器

动态编码器会生成多个ci，解码器需要根据当前生成的序列，自行选择关联度更高的ci，这也被称为注意力机制

注意力机制（Attetion）

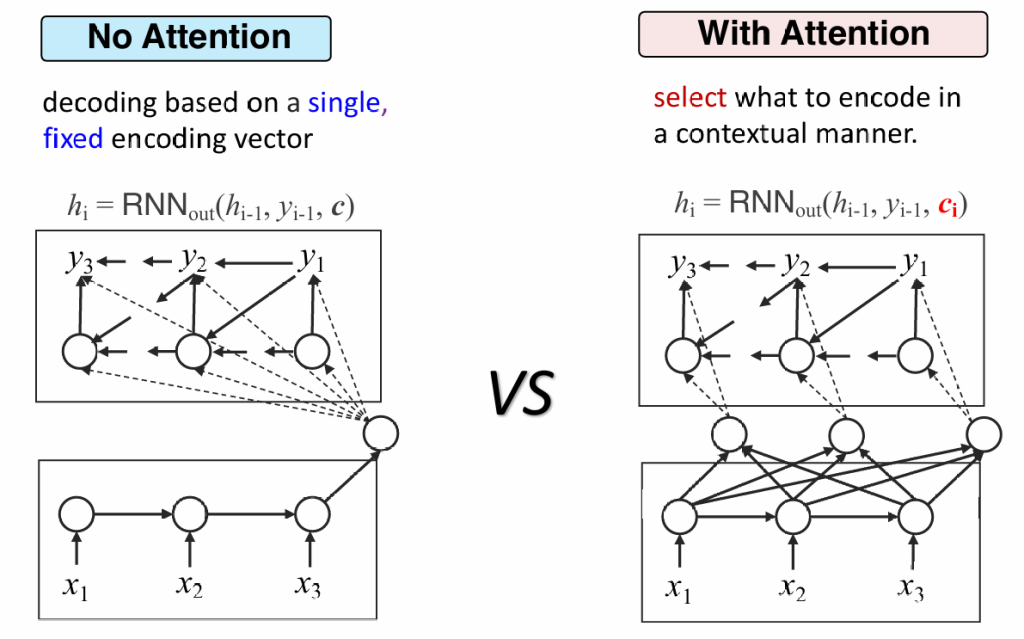
如何选择最合理的c？
——训练一个神经网络，输入为解码器的状态及所有c，输出所有c的分数，选择分数最高的

Transformer

具体步骤：
输入为x={x1,x2,…,xn}

将注意力机制进行拓展，我们希望在编码过程中也使用注意力机制，克服掉RNN不能并行的缺点。

1.编码

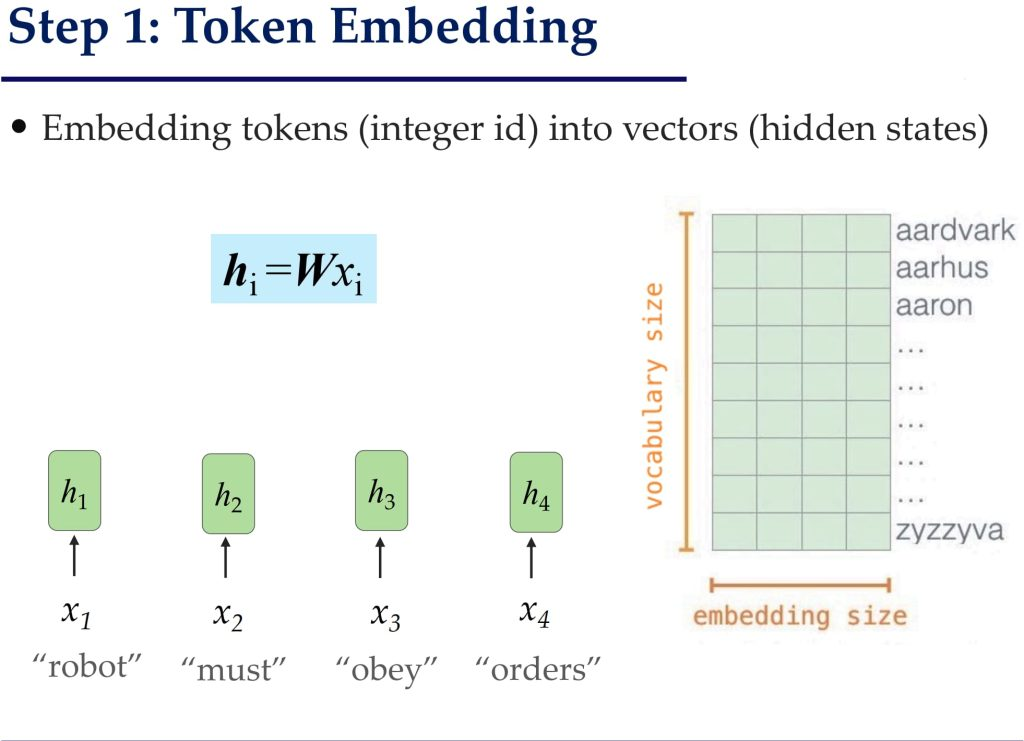
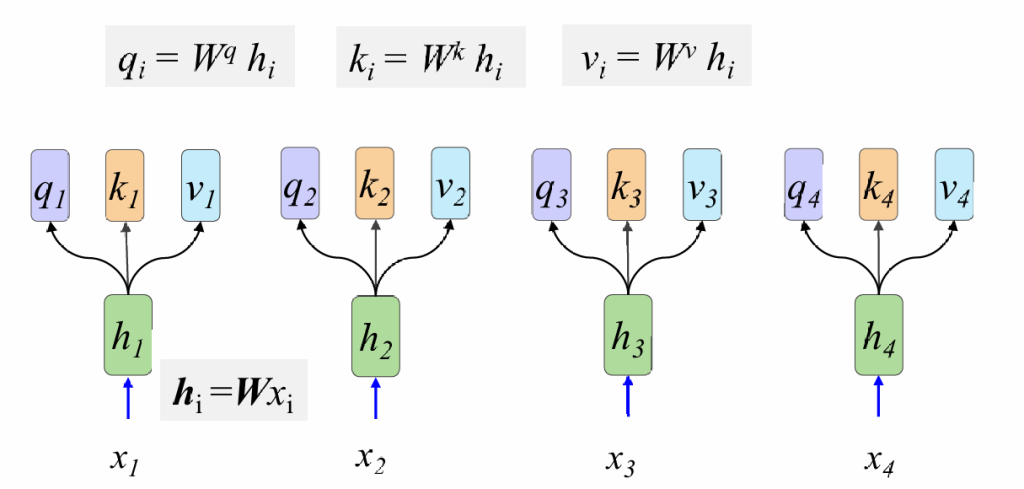
2.接着计算Q,K,V，其中Wq，Wk，Wv为三个可学习矩阵

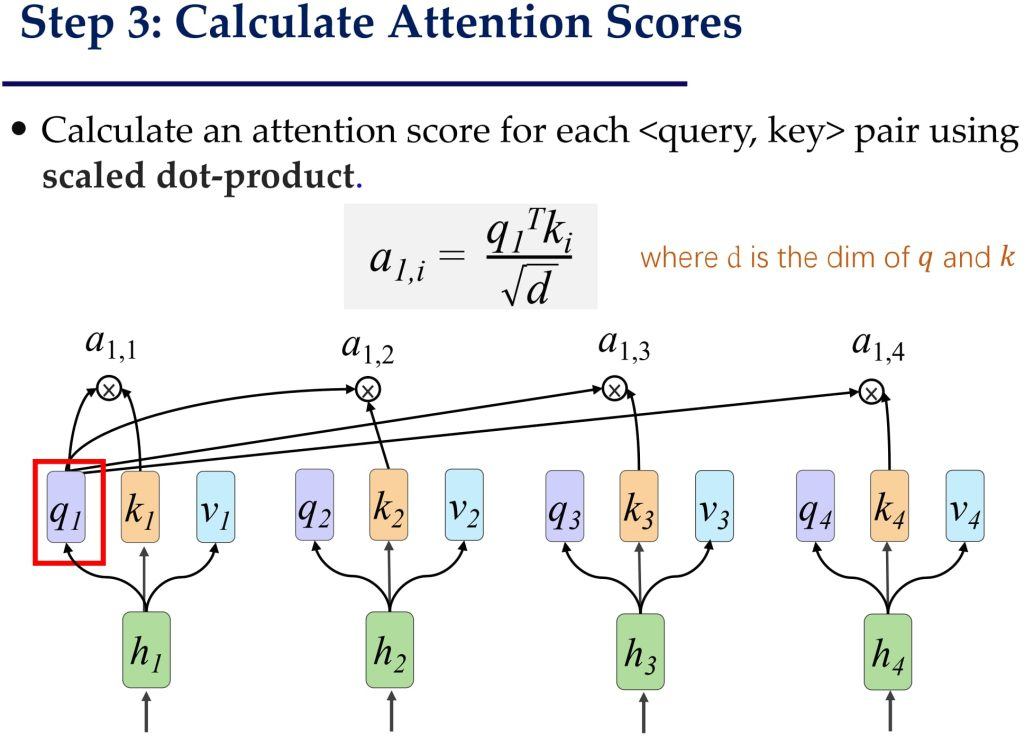
3.计算分数并归一化

这里以h1做query，用h1自己的q1分别于剩下的k1-ki计算a，然后通过softmax归一化（下面的公式）得到a1,i，其中d为q和k的维度

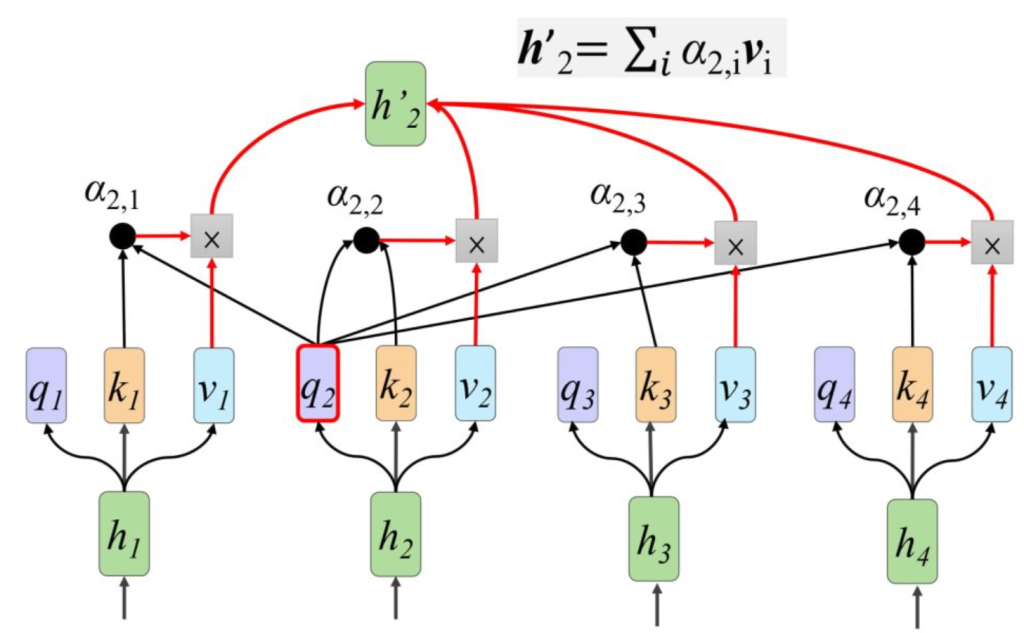
4.把得到的分数，value结合得到h1‘-hi’ ，最后合成大矩阵

对上面几步抽象成矩阵计算：

第一步：H=WX
第二步：Q=WqH；K=WkH；V=WvH
第三步：A=KTQ/\sqrt{d} ; A’=softmax(A)注意这里一定要除\sqrt{d}
假设原来是[10,20,30]，除\sqrt{d}后是[1,2,3]，前者softmax结果是[2.06106005e-09 4.53978686e-05 9.99954600e-01]，后者是[0.09003057 0.24472847 0.66524096]
第四步：H’=VA’

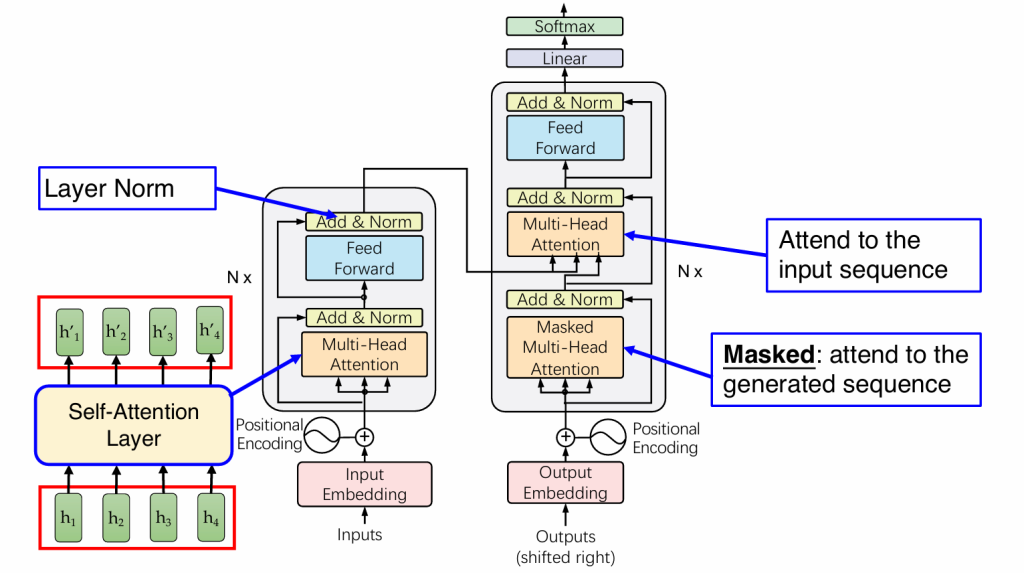
这些矩阵运算可以用gpu加速，但是上面的过程丢失了词语间的顺序，我们需要补充一个位置编码，将顺序作为模型输入（onehot编码，在哪一位哪一位就是1）

大语言模型LLM

预训练语言模型

在一些情况下，我们的数据量不足以训练一个transformer，选择先让模型理解自然语言，然后再在小数据上微调。对于最广泛的预训练模型BERT：

BERT的训练目标是理解自然语言，以此为基础的训练任务有两个：1.输入随机遮罩的句子，预测被遮罩的词语；2.给定两个句子，判断两句是否是上下文关系

微调应用：句子分类；词语标记；语句间关系预测；阅读理解Q&A；

大语言模型LLM

大模型微调；参数化微调（只更新一部分参数）；提示词工程；RAG检索增加生成（用户对数据进行筛选排序，然后和问题一起发给大模型

卷积神经网络CNN

机器如何识别图片？不能直接识别整个图片，因为杂乱信息太多影响判断
我们需要对图片特征提取，把特征喂给模型，但特征提取需要人工标注
解决：基于深度学习的自动特征提取

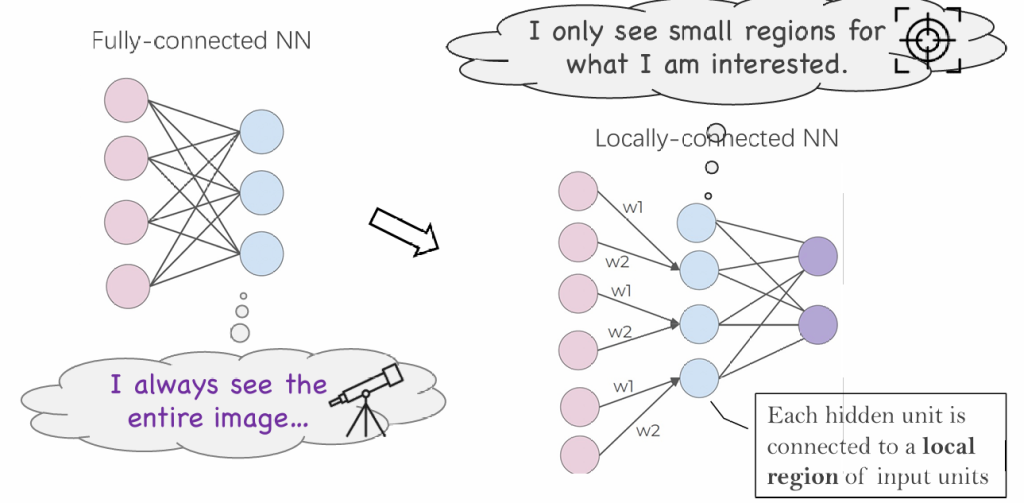
标准神经网络的问题：

  • 丢失图片的位置信息（整个图片是一个向量）
  • 关注整张图片，不会将注意力集中
  • 对于信息的位置敏感
  • 参数量过大

从MLP到CNN：首先简化全连接层，让网络关心局部特征

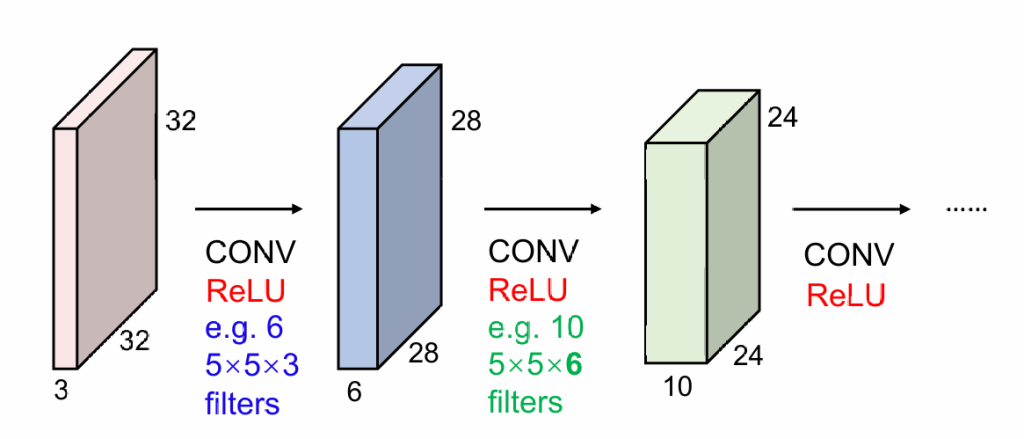
这个过程实际可以用卷积完成，将几个点的数据通过卷积合并成一个数据

实际情况下，因为图片有RGB三通道，所以实际我们做的是3维卷积。比如3*5*5的卷积核就会将75个值合并成1个

针对图片缩小的问题，我们采取填充(padding)的方式解决；

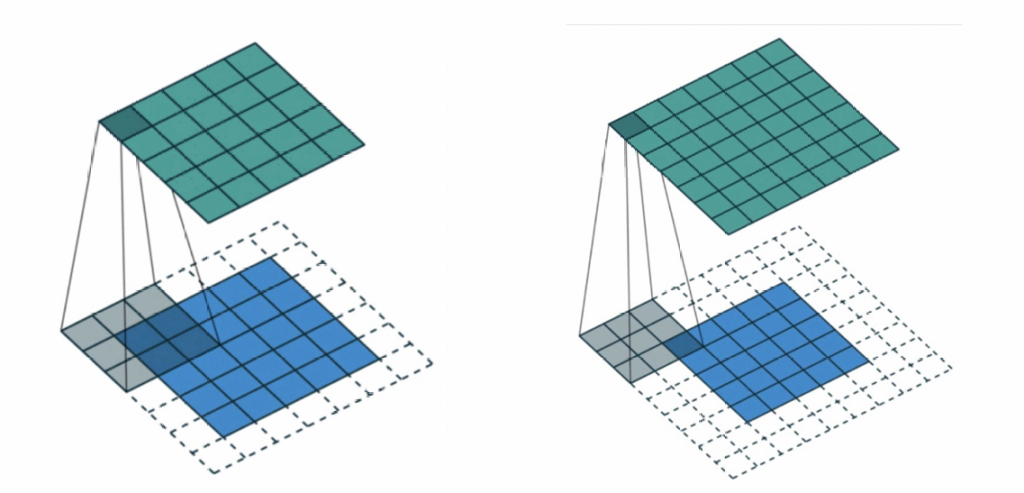
如果我们想缩小卷积后的大小，我们采用池化(pooling)，即卷积核跳过一些位置

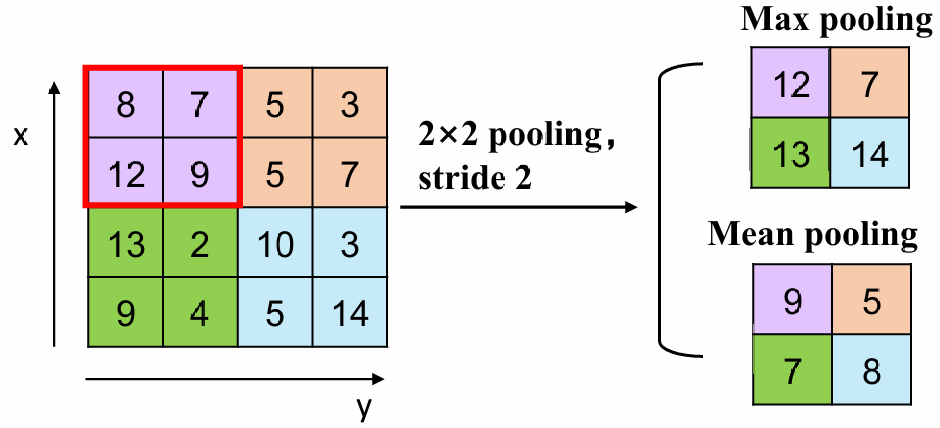
假设我们使用NN的原图片，FF的卷积核，填充宽度为P（如果宽度为1则边长为N+2），池化为S(stride)，则输出大小为(N+2P-F)/S

我们可以把用CNN处理文本（代替MLP）吗？——可以，用卷积核卷连续几个词向量

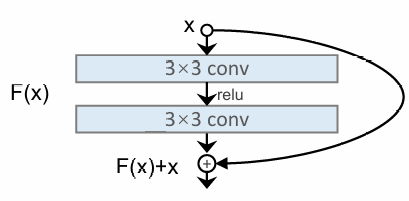
实践中发现在卷积层叠加到很高后，效果反而不如较少的层次，原因是后续的卷积层丢失了原有的信息，为此我们使用残差网络，将原始数据和卷积后的数据都传播到后面

机器视觉CV

机器视觉的任务：图片分类、图片分割、物体识别、图升文、文生图

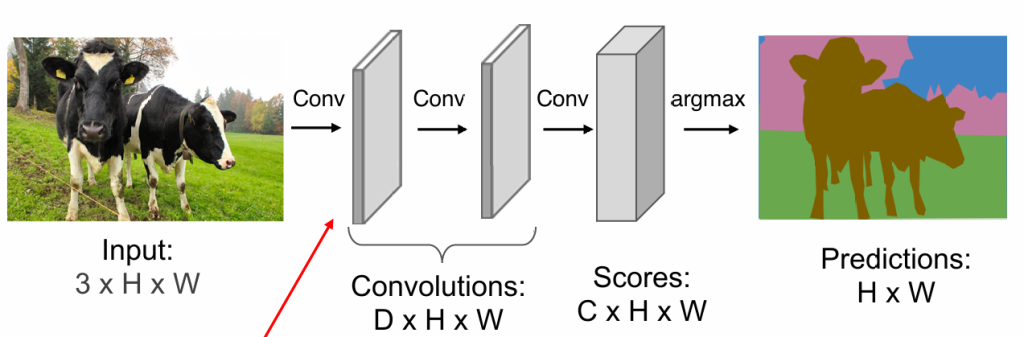
图片分割

显然我们不能让模型对单独的一个像素进行分类，因为几千万像素不能逐一进行分类
——我们能否通过卷积神经网络，得到特征，然后得出分类

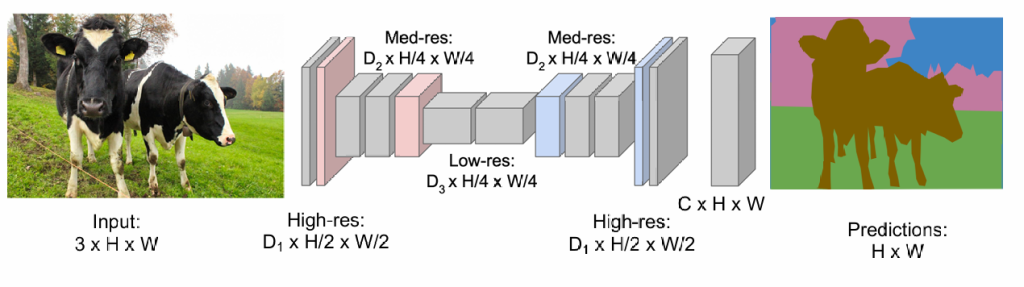
我们似乎没有必要对整个图片进行划分，我们可以先在小图片上划出轮廓，再复原大图片

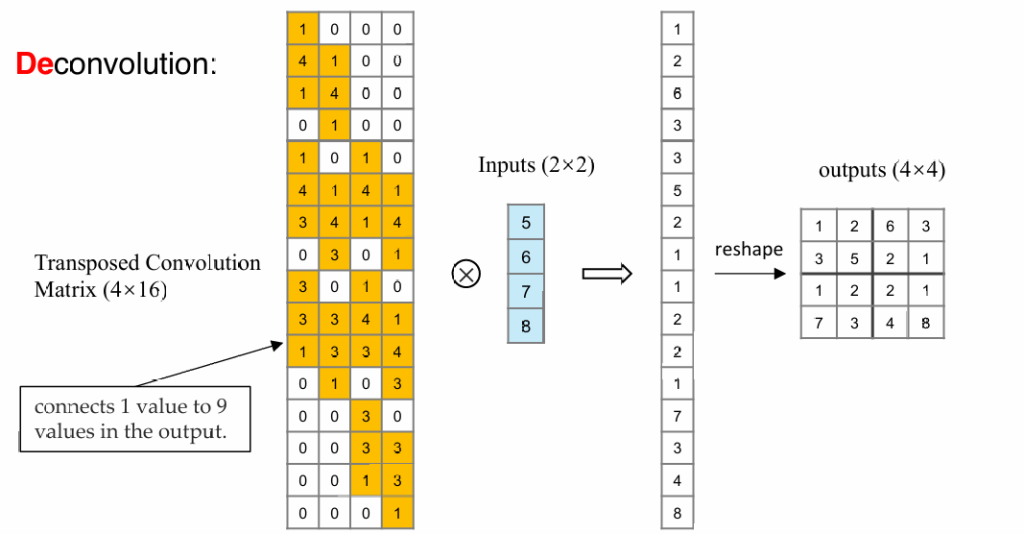
现在我们考虑如何复原图片(unpooling)：
从正向的卷积来看，我们可以通过将图片及卷积核铺开，将卷积操作变成矩阵Cm×n与向量i的乘法

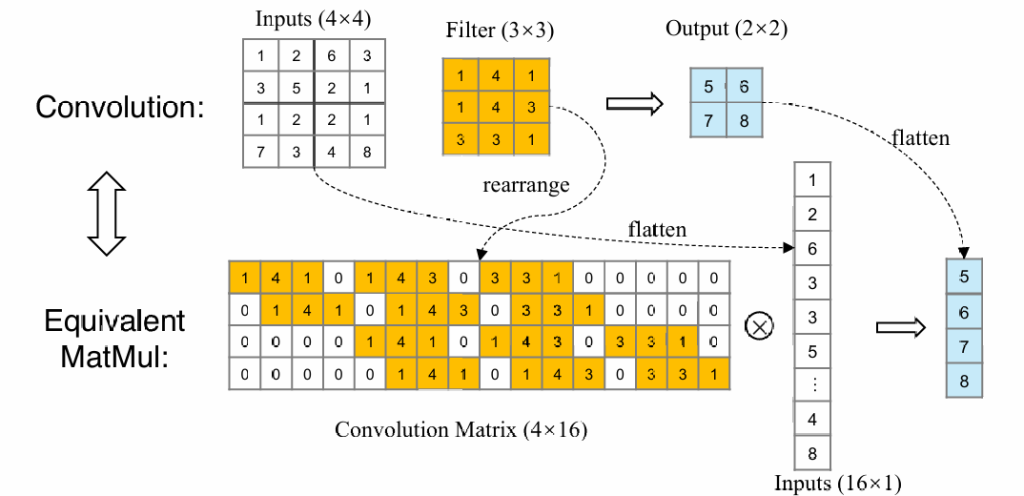
可以通过反向乘一个n×m的矩阵，将卷积后的结果复原成原始图片的大小（注意不能完全复原成原始图片，需要学习矩阵参数）

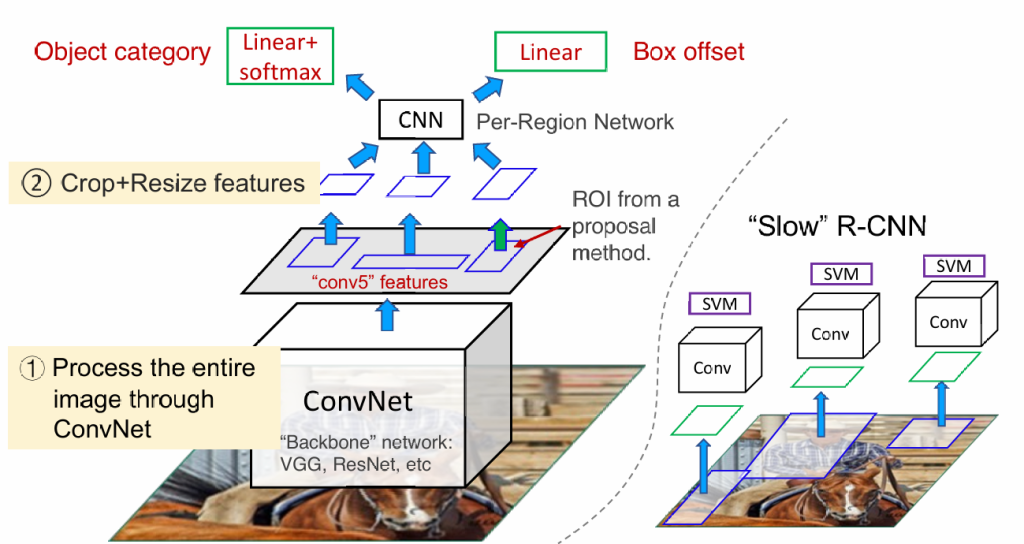
物体识别

识别=分类+定位

分类很好解决，只需要训练一个分类器；主要问题是如何划分图片？

我们使用“selective search”——一个传统的机器视觉算法，能够给出可能出现目标的范围

当我们获得这些分块的小图片，我们对这些图片进行卷积可以完成目标(slow r-cnn)，但我们仍觉得分块过于多，所以我们先对整张图进行一次卷积，再根据小分块裁剪卷积结果，提升运行速度(fast r-cnn)

除此之外，我们还可以通过训练神经网络进行图片划分(faster r-cnn)，还有一些其他算法可以提升速度（YOLO）

图生文

类似于翻译问题，我们仍拆分成编解码器，参照transformer，将图片通过卷积神经网络提取特征，然后接入自注意力机制；甚至可以直接将分块的原始图片输入给transformer，不使用卷积神经网络（Vision Transformer-ViT）

视觉语言模型VLM

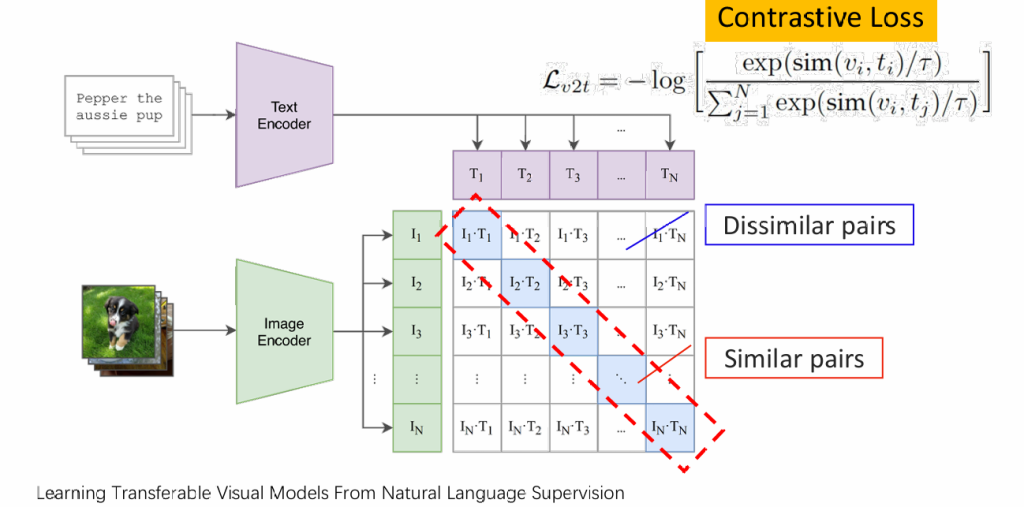
在ViT中我们发现transformer不仅能理解文字，还能理解图片，那么我们可以训练一个支持多种类型输入输出的transformer

clip：对文字和与之对应的图片采用两个encoder进行编码，最大化两组编码的相似度

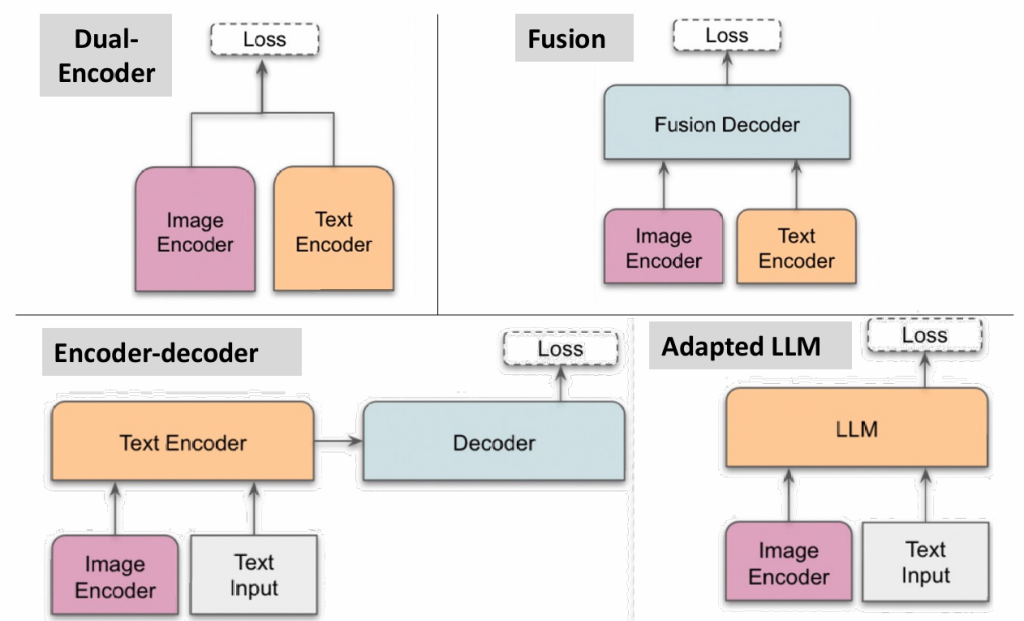
CLIP对应下图中的左上角，还有些不同的架构

聚类

希望在没有标签的情况下，让模型自行将数据分类。在大规模数据中，我们无法使用k-近邻算法，因为存储难度太大，我们选择记录只每个簇的圆心。

k-means把簇的圆心定义为簇内点的均值，需要人为给定k

k-均值算法由以下四步来完成:

  • 随机的选择k个对象作为目前划分的簇的初始簇中心
  • 对剩下的每个对象，计算与各簇中心的欧氏距离，将它分配到最相似的簇
  • 使用上次迭代分配到该簇的对象，计算新的均值
  • 使用新的均值作为新的簇中心，重新分配所有对象，直到分配稳定

复杂度：O(Iknd)；其中n 是对象的数目, k 是簇的数目, I 是迭代的次数, d是向量的维数

受初始中心的影响，可能导致迭代次数增加或陷入局部最优

优点：有可解释性，效率高
缺点：每个簇都是球形，在一些抽象数据中，“均值”难以定义，k需要人工指定，不一定合适，对异常值敏感

降维

降维方法：PCA主成分分析（线性）Autoencoder自编码器（非线性）

以以下数据为例
A = [2.5, 2.4]
B = [0.4, 0.7]
C = [2.2, 2.9]

1.计算样本均值X及协方差矩阵S

\bar{x}=\begin{bmatrix}\frac{2.5+0.4+2.2}{3} & \frac{2.4+0.7+2.9}{3}\end{bmatrix}=\begin{bmatrix}1.7 & 2\end{bmatrix}

定义协方差及协方差矩阵(以2维为例，若三维则为xyz)，(n为样本数量)

cov(X,Y)=\frac{\sum_{i=1}^{n}(X_i-\bar{X})(Y_i-\bar{Y})}{n-1}
S_{n\times n}=\begin{bmatrix}cov(x,x) & cov(x,y) \\ cov(y,x) & cov(y,y)\end{bmatrix}

在例子中：

cov(x,x)=\frac{(2.5-1.7)^2+(0.4-1.7)^2+(2.2-1.7)^2}{3-1}=1.26 \\cov(x,y)=cov(y,x)=\frac{(2.5-1.7)*(2.4-2)+(0.4-1.7)*(0.7-2)+(2.2-1.7)*(2.9-2)}{3-1}=1.23 \\cov(y,y)=\frac{(2.4-2)^2+(0.7-2)^2+(2.9-2)^2}{3-1}=1.33
S=\begin{bmatrix}1.26 & 1.23 \\1.23 & 1.33 \\\end{bmatrix}

2.解出协方差矩阵S的特征值λ，即|S-λI|=0的解

\mid S-\lambda I\mid =\begin{vmatrix}1.26-\lambda & 1.23 \\1.23 & 1.33-\lambda \end{vmatrix}=(1.26-\lambda)(1.33-\lambda)-1.23^2=0

解二元一次方程得

\lambda_1={0.06}\quad \lambda_2={2.53}

进而得到与λ对应的特征向量（即Sv=λv）

特征向量满足如下式子：

Sv=\lambda v\\(S-\lambda I)v=0

需要设v=[x,y]然后解出x,y的比例，再归一化到单位长度

对于λ1：

\begin{bmatrix}1.26-0.06 & 1.23 \\1.23 & 1.33-0.06 \\\end{bmatrix} \begin{bmatrix}x \\y \\\end{bmatrix} =0

解得

\frac{x}{y}\approx -\frac{1.23}{1.2} \approx -\frac{1.27}{1.23}

以上两个约等于是因为计算误差导致的，实际上会是一个值。
再进行归一化，v1=[0.713,-0.696]

对于λ2同理，v2=[0.696,0.713]（因为是2维所以可以直接看出来，三维不行）

两个主成分的表示：

F_1=v_{11}(x-\bar{x})+v_{21}(y-\bar{y}) = 0.713(x-1.7)-0.696(y-2)\\F_2=v_{12}(x-\bar{x})+v_{22}(y-\bar{y}) = 0.696(x-1.7)+0.713(y-2)

主成分的贡献度p：（经证明主成分的方差就是特征值大小）

p_i=\frac{\lambda_i}{\sum \lambda_i}

对示例情况：

F1贡献度=0.06/(0.06+2.53)=0.02
F2贡献度=2.53/(0.06+2.53)=0.98

可以根据贡献度从大到小，对所有主成分进行排序，然后根据累计贡献度要求选出前几个主成分

Autoencoder自编码器

自编码器是一个神经网络，其输出目标是还原输入

PCA算法可以抽象成一对编解码器

实际的自编码器，编解码器是需要训练的神经网络

我们可以使用自编码器完成图片复原、相似图片搜索等功能，以及用于CNN

生成式模型

GAN

回忆：语言模型也是生成式模型，我们学习的是下一个词语的概率
仿照语言模型，我们在生成其他数据如图片时，学习的也是概率

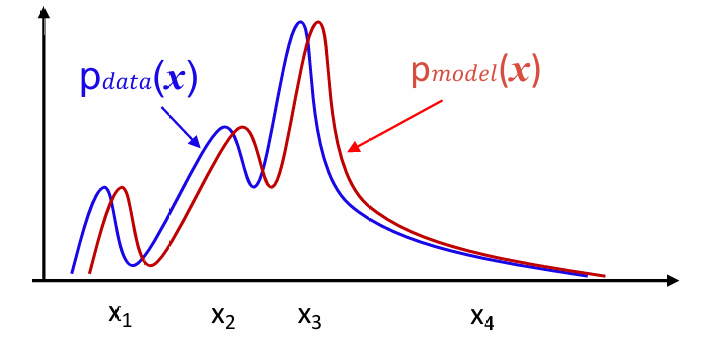
问题：
我们如何表示图片的概率
我们如何使pmodel接近pdata

表示图片的概率：

我们通过随机数让生成器G产生图片，就如同掷色子，通过大量的生成的图片的分布反映概率分布

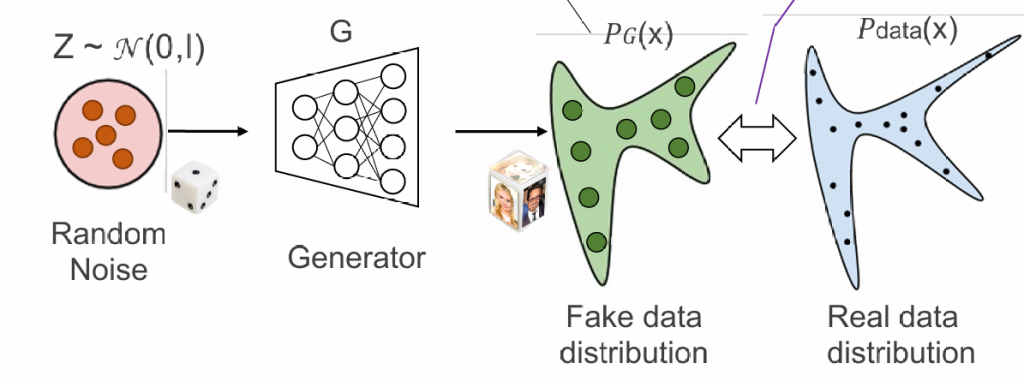
使pmodel接近pdata：

即希望模型只生成真图片，不生成假图片，生成的假图片越少，说明二者的概率分布越接近

引入一个判别器：判断一张图片是否由ai生成，当生成模型可以以假乱真，那么说明分布是一致的。
在这种情况下，生成器和判别器的目标是相反的，二者构成了“生成对抗网络”GAN

判别器的训练：（损失函数使用交叉熵定义）

生成器的训练：（损失函数与判别器相反）

因为生成器看不到真实图片，所以少了一项

需要注意的是，训练开始时，需要有一个已经预训练过的判别器，否则训练结果不好。

深度卷积生成对抗网络DCGAN

使用逆向卷积作为生成器，使用卷积神经网络作为判别器

针对DCGAN，研究人员发现了一些有趣的现象。
加上我们训练好了一个生成器，然后我们已知某些随机种子对应着生成某类图片；当我们给这些种子进行线性组合，生成的图片仍是这个类型；甚至，类间的随机种子加减后的结果能反映出图片类型的增删

Conditional GAN

能够按照需求生成图片

我们把条件分别输入生成器和判别器，然后进行训练，也可以看作一种翻译器

CycleGAN

Conditional GAN是监督学习，需要大量的成对数据，而cycleGAN的目标是无监督学习。在没有成对示例的情况下将图像从源域 A 传输到目标域 B。

GAN本质上是一个从随机分布到图片概率分布的概率转换器；而CycleGAN需要的是从图片概率分布到图片概率分布的概率转换器

模型结构：

通过反向生成器GBA尝试复原图片，最大化复原图与原图的相似度；GAB训练目标不变。如果GBA能复原图片，说明生成的假图片一定包含了原图的信息

变分自编码器Variational Autoencoder-VAE

GAN生成图片需要随机变量z，但是我们找不到z的规律，无法通过定向需求产生图片
我们想到使用Autoencoder，使z是一张原始图片的压缩表示，这样的z是有意义的，可以用来定向生成图片，但是Autoencoder中z是离散分布的，我们要想办法让z的分布式连续的，比如符合高斯分布

VAE：强制编码器输出均值和标准差（可以确定为一个高斯分布），解码器的输入是符合这个高斯分布的一个随机值；这样训练出的模型会将特征隐藏在高斯分布中，而满足这种高斯分布的随机种子生成的图片具有相同的特征，但又各不相同。

GAN和VAE的局限性：降维后的z的表达能力有限，和原始图片差别非常大；所有内容都是一次生成的

去噪扩散模型

希望模仿人类的绘画过程，一步步生成图片

模型结构：原始图片是随机噪声，经过多层生成器得到图片

训练过程：在一张图片上随机添加噪声点，再训练模型将其复原（对每一层分别训练，而不是一起训练）

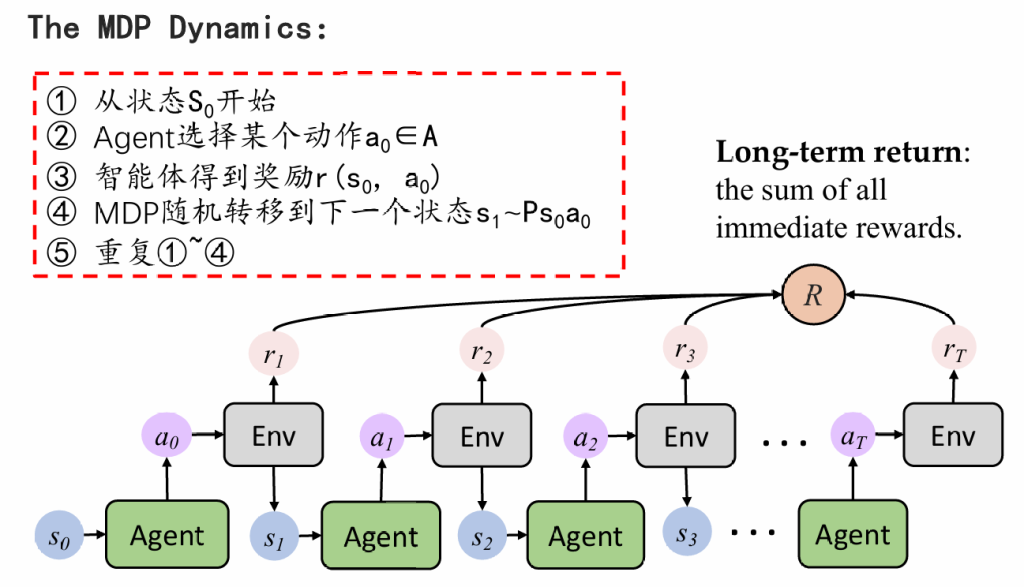
强化学习RL

agent生成一个action，环境返回state和reward；agent再根据state生成新的action

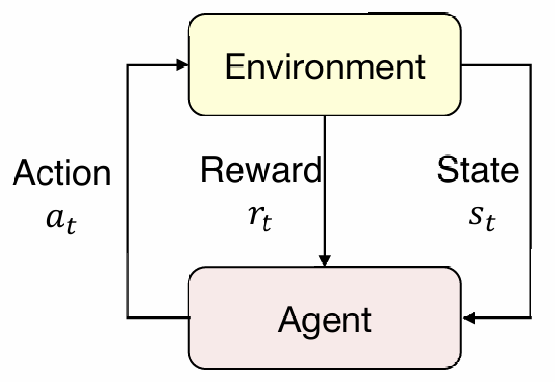
定义马尔科夫决策过程：

把训练抽象为如下多次决策，每次决策会带来状态专业，并获得一定奖励或者惩罚，我们最终的目标是找到一条奖励最大的路径

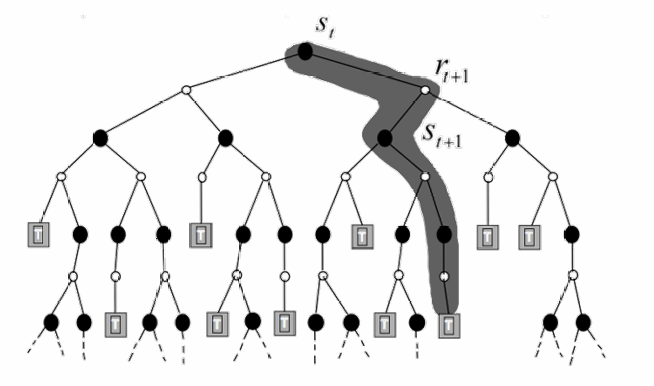
RL的学习过程：

Q-Learning

定义：Q函数：输入为当前状态和行为，输出为未来可获得奖励的期望

如何得到Q值：
1.蒙特卡洛：通过遍历后续所有情况/随机计算几种后续情况，计算平均的奖励值；但是会耗费大量时间
2.递归估计：根据递推关系Qt=rt+γmaxa{Qt+1}，采用动态规划的方式，填写一个Q值表，直至表填满（递归关系不唯一）

Q函数的问题：只能适用于走格子这种简单的游戏，我们无法将Q值表真正填满，因此我们使用神经网络来拟合Q函数

DQN

损失函数：

在训练过程中，我们存储状态转移的四元组D = {(s(1),a(1), r(1), s’(1)), …, (s(N) , a(N), r(N), s’(N))}，DQN在对整个D进行优化时的损失函数：

  • mini-batch : DQN 会随机抽取一批经验进行训练，而不是使用最新的经验，即minibatch

问题：Q也是根据模型变化的，目标值不稳定，于是我们另外指定一个网络（target Net），专门用于生成Q，整个网络的参数是固定的，每隔一段时间将Q Net的参数复制过去。

训练流程：

  • 初始化：初始化Q网络和参数θ：
  • 智能体与环境交互：
    • 在当前状态s，智能体，使用贪婪策略选择动作a
    • 执行动作a，观察奖励r和下一状态s‘。
    • 把(s,a,r,s′) 存入经验回放缓冲区。
  • 训练Q网络：
    • 从回放缓冲区中随机抽取一批经验 (𝑠,𝑎,𝑟,𝑠′)。
    • 计算目标的Q值，下图Target Qvalue
    • 最小化Q网络的预测误差，通过lossfunction
  • 更新目标网络：定期将 Q 网络的参数 θ 复制到目标网络 θ−。
  • 再重复上述过程
  • 优点：
    • 能够处理高维状态空间（比如图像）。
    • 使用深度学习方法来近似 Q 函数，解决了传统 Q-Learning 的局限性。
    • 引入了目标网络和经验回放，提升了训练的稳定性。
  • 缺点：
    • 对超参数敏感（比如学习率、折扣因子等）。
    • 训练过程可能不稳定，尤其是在复杂环境中。
    • 计算资源需求较高，因为需要多次更新神经网络。

策略学习

我们希望直接通过环境S得出行动a，或者说给出对于某一个行动ai的概率，即 $ \pi_\theta(s) \sim P(a|s) $

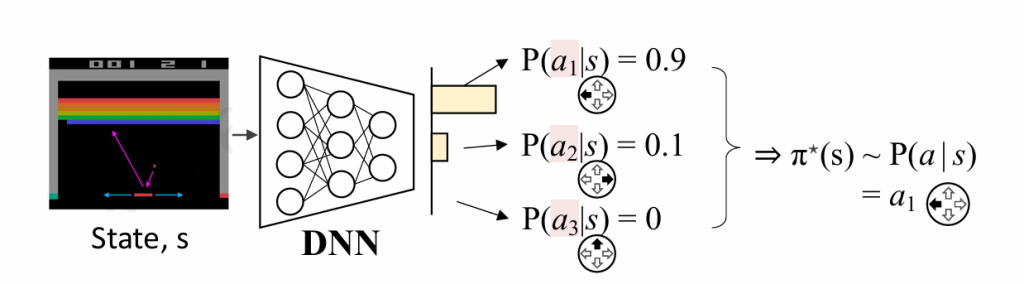
转换成了一个分类问题，我们使用未来能获得最大评价奖励的a作为目标值。
我们还是通过多次实验的方式得到平均的reward

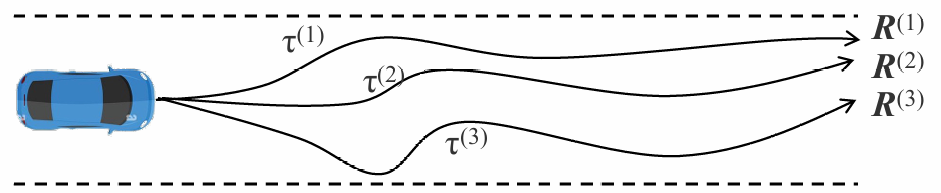
策略梯度的损失函数：

$ L = -\sum_{\tau} R_\tau \log p_\theta(a_t|s_t) $

对其求梯度，可以得到

$ \nabla_\theta L = -\sum_\tau R_\tau \nabla_\theta \log p_\theta(a_t|s_t) $

那么最后参数更新及梯度表示：

基于RL的文本生成

传统的文本生成方法（如基于 RNN、LSTM 或 Transformer 的语言模型）主要通过最大化条件概率来生成下一个词语；强化学习提供了一种机制，可以根据生成文本的全局质量来优化模型。我们希望最大化整个生成序列的总奖励R，而不是单纯的最大化词语的条件概率。

作业解析

作业一

第一题

考虑一下根据年龄和薪水预测一个人是否拥有大学学位的问题。下表和图表包含10个人的训练数据。

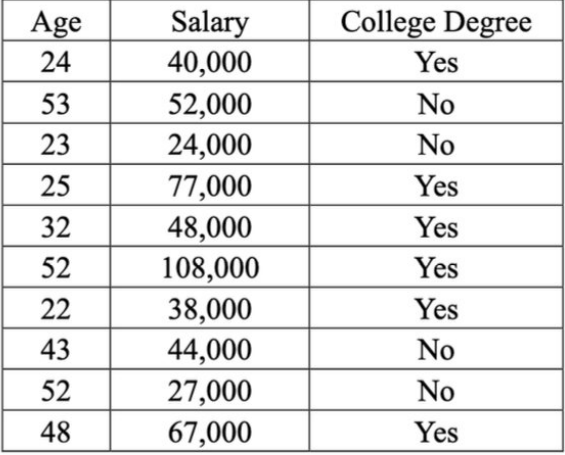
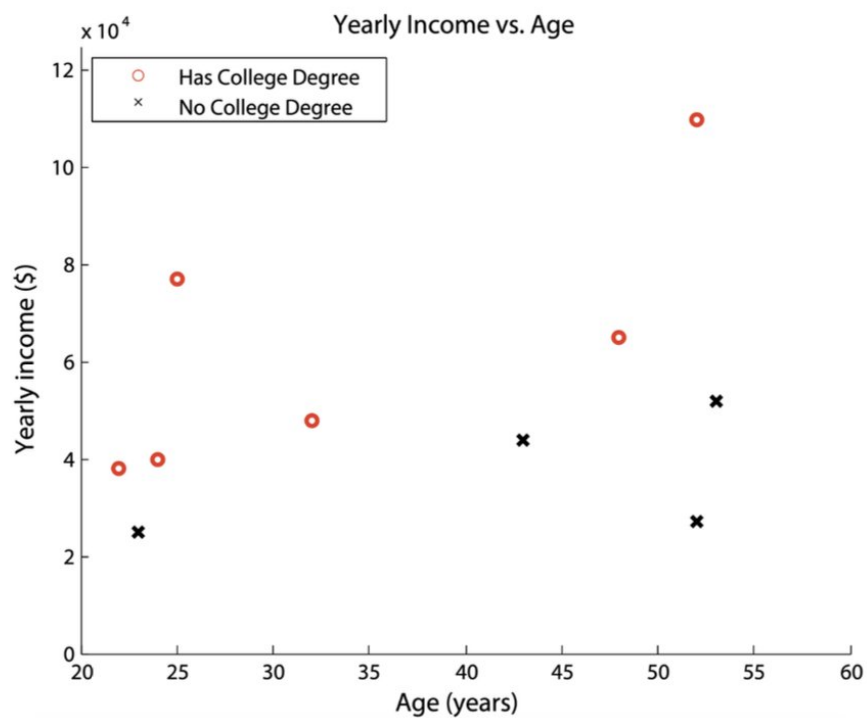
构建决策树

通过贪婪地分割属性来最大化信息获取，构建一个决策树来分类一个人是否拥有大学学位。假设每个分割的阈值是当前子集中属性的中间值，即½（min+max）。显示每次分割的信息增益，并在图中绘制所学树的决策边界。

解答：

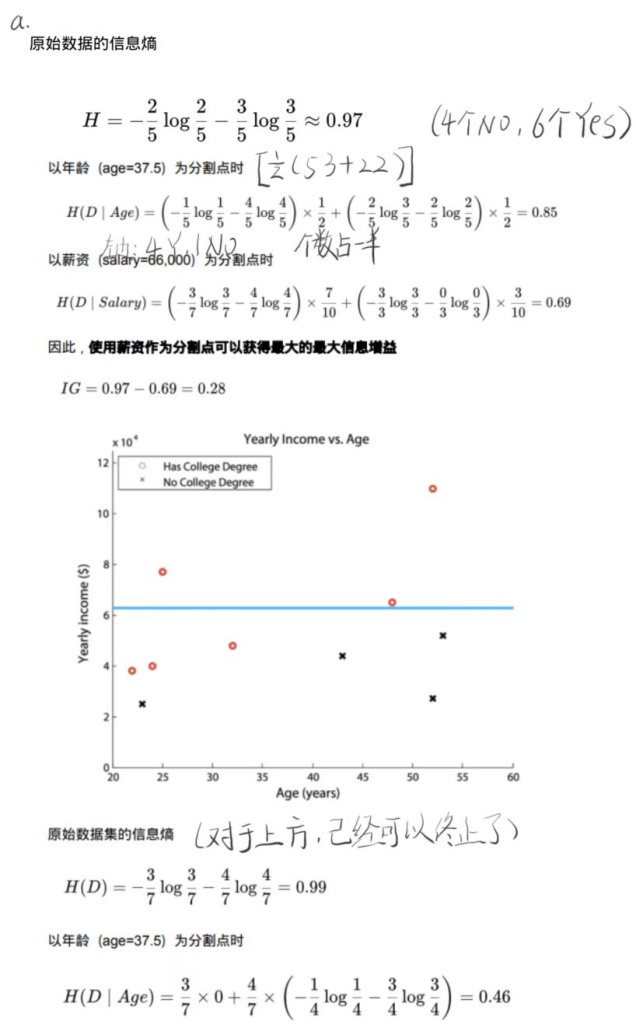
多元决策树

多元决策树是单变量决策树的推广，其中每个分割的决策规则中可以使用多个属性。也就是说，分割不需要与特征的轴正交。
对于相同的数据，提供一个多元决策树，其中每个决策规则都是一个线性分类器，根据αxage+βxincome-1的符号做出决策。

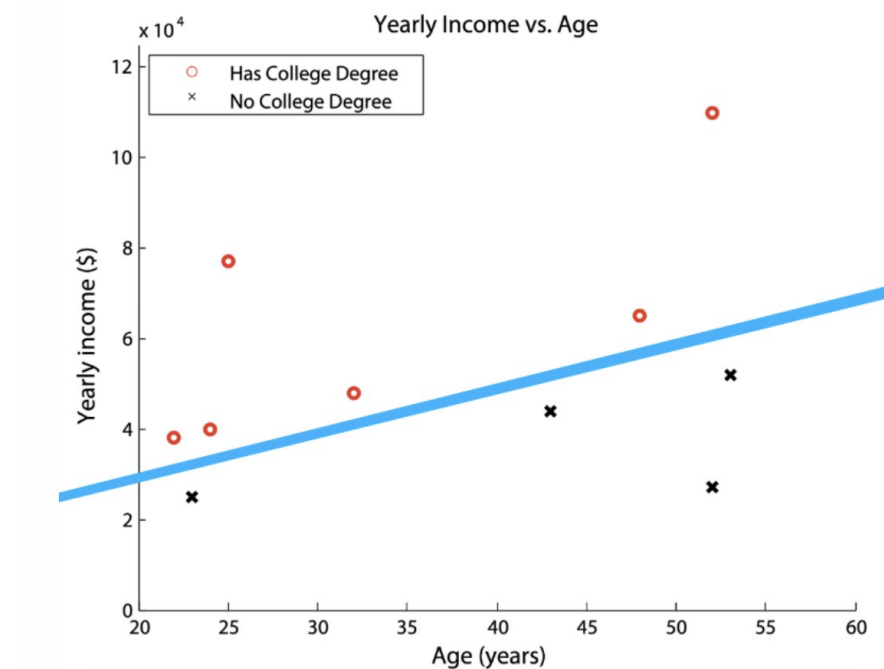
解答：只需要选择一个合适的参数，使得线满足把两类完全分开

例如α=-0.1，β=-0.0001，那么信息增益计算为 IG=0.97-0=0.97

k-最近邻

假设我们使用标准欧几里德距离来计算最近邻，则绘制1-最近邻分类器的决策边界。

解答：做垂直平分线，连接合并，深色的就是最后结果。

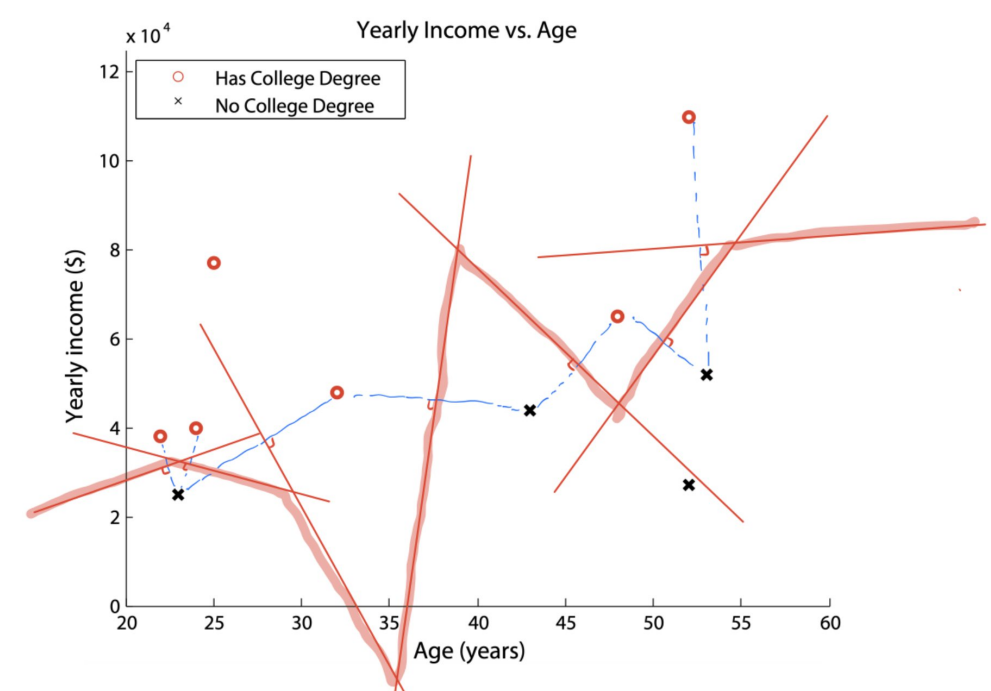
第二题

朴素贝叶斯分类

朴素贝叶斯分类器广泛应用于文本分类。在这个问题中，你会得到一组学生对食堂的反馈，并附有相应的标签，表明学生是喜欢还是不喜欢它。

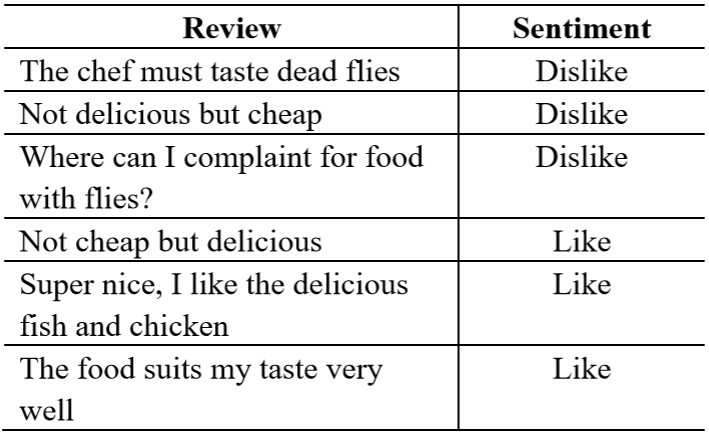
现在给出一个新的评论“very delicious and cheap”，我们想使用朴素贝叶斯算法将它们分为两类。请提供整个计算过程。

解答：

带 Laplace 平滑的条件概率：

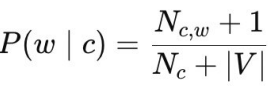
作业二

第一题

设计一个两层多层感知器（MLP），用于检测输入 x1, x2, x3, x4 ∈ R 中 是否存在一对 xi + xj = 0（其中 i = j）。如果存在这样的数对，网络输出 1；否则输出 0。 隐藏层使用冲激激活函数σ ：

输出层选择使用阶跃激活函数σ ′

隐藏单元数量

n的合适值是多少（即隐藏单元的数量）？解释原因

解答：

问题要求检测 x1, x2, x3, x4 中是否存在一对 xi + xj = 0，也就是说我们需要检查所有可能的数对组合 (𝑥𝑖,𝑥𝑗)，并判断它们的和是否为零。

对于四个输入，可能的数对（i ≠ j）有：(x1, x2),(x1, x3),(x1, x4),(x2, x3),(x2, x4),(x3, x4)
所以设计网络，使得每个隐藏单元负责检查一个数对，计算 xi + xj 并 应用冲激激活函数。因此，需要 6 个隐藏单元，每个对应一个数对：n=6

权重和偏置

选择一组权重和偏差，以便网络正确实现所需功能。

解答：

设计一个具有 n = 6 个隐藏单元的网络，每个隐藏单元对应一个数对。
设隐藏单元为 h1, h2, . . . , h6，分别对应数对 (x1, x2),(x1, x3),(x1, x4),(x2, x3),(x2, x4),(x3, x4)。

对于隐藏单元 hk，其预激活值ak是输入的加权和加偏置，即：

ak​=wk1​x1​+wk2​x2​+wk3​x3​+wk4​x4​+bk​

对于输出层：

输出层需要根据隐藏层的输出 ℎ1,ℎ2,…,ℎ6​ 判断是否存在至少一个数对满足 𝑥𝑖+𝑥𝑗=0。如果存在，输出 𝑦=1；否则输出 𝑦=0

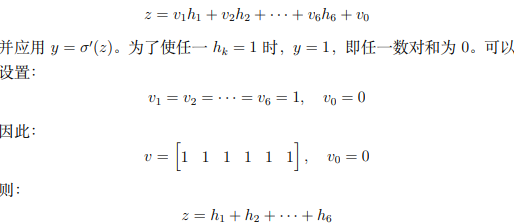
这正是我们需要的逻辑：当存在至少一个数对满足 𝑥𝑖+𝑥𝑗=0，隐藏层的某个 ℎ𝑘=1，从而 𝑧>0，输出 𝑦=1。否则，所有 ℎ𝑘=0，从而 𝑧=0，输出 𝑦=0。

验证分类

验证三个测试网络：
– 输入 1：x1 = 1, x2 = −1, x3 = 2, x4 = 3
– 输入 2：x1 = 2, x2 = 3, x3 = 4, x4 = 5
– 输入 3：x1 = 0, x2 = 5, x3 = −5, x4 = 0

解答：

逻辑都类似，逐个验证展示即可

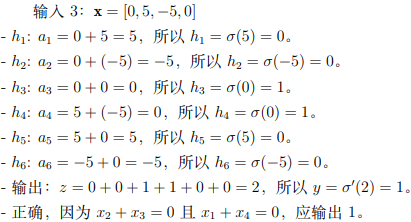
第二题

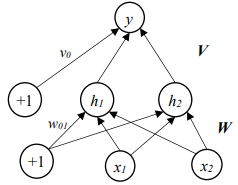
前向传播

要计算前向传播，就需要算出实际的a1，a2，然后按照要求使用激活函数得出隐藏层h1h2。

做题就是按照公式组合，比如说第一个可以看到h1是由x1,x2,w0,W共同组合成，因此我们就可以先计算出a1，然后激活后作为h1，同理，对于y，由h1,h2,v0,V这个组成，还是组合后激活得到y

解答：

反向传播

使用第 4 个样本 (x = [0.7, 0.6],t = 1)，基于交叉熵损失函数计算每个参数的偏导数

解答：

通过查询可知，交叉熵损失函数L = −tlog y − (1 − t)log(1 − y)，因为t=1，所以L=-logy

（1）对于误差信号δy，为损失函数对输出y的偏导数：

$ \delta_y = \frac{\partial L}{\partial y} $

带入上面的交叉熵损失函数L=-logy，可以得到
$ \delta_y = \frac{\partial (-\log y)}{\partial y} = -\frac{1}{y} = -\frac{1}{0.470} \approx -2.128 $

（2）接着对于δz，由之前可得z激活后得到输出的y，即：

$ y = \text{sigmoid}(z) = \frac{1}{1 + e^{-z}} $

对z求导，得到：
$ \frac{\partial y}{\partial z} = y(1 – y) $

误差信号从 y 传递到 z 使用链式法则：
$ \delta_z = \frac{\partial L}{\partial z} = \delta_y \cdot \frac{\partial y}{\partial z} = \delta_y \cdot y(1 – y) $

上一问得到的y和刚才的δy代入后，得到：
$ \delta_z = -2.128 \cdot 0.470 \cdot 0.530 \approx -0.530 $

（3）对于输出层权重vkV0的偏导数

输出层的预激活值 z 是隐藏层的加权和加偏置：
$ z = v_1 h_1 + v_2 h_2 + v_0 $

每个权重 𝑣𝑘​ 的偏导数为：
$ \delta v_k = \frac{\partial L}{\partial v_k} = \delta_z \cdot \frac{\partial z}{\partial v_k} $

求导后可以发现：
$ \frac{\partial z}{\partial v_k} = h_k $

那么：
$ \delta v_k = \delta_z \cdot h_k $

那么再用到上面的h1，h2，和上一问的δz，可以得到
$ \delta v_1 = \delta_z \cdot h_1 = -0.530 \cdot 0.07 \approx -0.0371 $
$ \delta v_2 = \delta_z \cdot h_2 = -0.530 \cdot 0.58 \approx -0.3074 $
$ \delta v_0 = \frac{\partial L}{\partial v_0} = \delta_z \cdot \frac{\partial z}{\partial v_0} = \delta_z \cdot 1 = -0.530 $

（4）对隐藏层输出hk​ 的偏导数

$ \delta h_k = \frac{\partial L}{\partial h_k} = \delta_z \cdot \frac{\partial z}{\partial h_k} $

其中从上一问式子中也可以看到，$ \frac{\partial z}{\partial h_k} = v_k $

代入题目中最开始给的v1，v0，还有上上一问的δz，最后得到
$ \delta h_1 = \delta_z \cdot v_1 = -0.530 \cdot 1.0 = -0.530 $
$ \delta h_2 = \delta_z \cdot v_2 = -0.530 \cdot (-0.5) = 0.265 $

（5）对隐藏层激活值ak的偏导数

隐藏层激活值 ak​ 是隐藏层输出 hk​ 的输入。隐藏层的激活函数是 ReLU，定义为：
$ h_k = \text{ReLU}(a_k) =
\begin{cases}
a_k, & \text{如果 } a_k > 0 \\
0, & \text{否则}
\end{cases} $

ReLU 的导数为：
$ \frac{\partial h_k}{\partial a_k} =
\begin{cases}
1, & \text{如果 } a_k > 0 \\
0, & \text{否则}
\end{cases} $

a1​=0.07>0, 𝑎2=0.58>0:
$ \delta a_1 = \delta h_1 \cdot \frac{\partial h_1}{\partial a_1} = -0.530 \cdot 1 = -0.530 $
$ \delta a_2 = \delta h_2 \cdot \frac{\partial h_2}{\partial a_2} = 0.265 \cdot 1 = 0.265 $

（6）对隐藏层权重 wjk​ 的偏导数

隐藏层的激活值 ak​ 是输入的加权和加偏置：
$ a_k = w_{k1} x_1 + w_{k2} x_2 + w_{k3} x_3 + w_{k4} x_4 + w_{0k} $

每个权重 wjk​ 的偏导数为：
$ \frac{\partial L}{\partial w_{jk}} = \delta a_k \cdot \frac{\partial a_k}{\partial w_{jk}} $

可以得到$ \frac{\partial a_k}{\partial w_{jk}} = x_j $，所以：
$ \delta w_{jk} = \delta a_k \cdot x_j $

代入，最后可以得到这四个数
$ \delta w_{11} = \delta a_1 \cdot x_1 = -0.530 \cdot 0.7 \approx -0.371 $
$ \delta w_{12} = \delta a_1 \cdot x_2 = -0.530 \cdot 0.6 \approx -0.318 $
$ \delta w_{21} = \delta a_2 \cdot x_1 = 0.265 \cdot 0.7 \approx 0.1855 $
$ \delta w_{22} = \delta a_2 \cdot x_2 = 0.265 \cdot 0.6 \approx 0.159 $

同理w0k偏导数

$ \frac{\partial L}{\partial w_{0k}} = \delta a_k \cdot \frac{\partial a_k}{\partial w_{0k}} = \delta a_k $

所以最后：
$ \delta w_{01} = \delta a_1 = -0.530 $
$ \delta w_{02} = \delta a_2 = 0.265 $

权重更新

设学习率为 η = 0.5，更新每个参数

解答：

梯度下降的更新公式为：
$ \theta \leftarrow \theta – \eta \cdot \frac{\partial L}{\partial \theta} $

按照之前计算的梯度一个个代入即可：

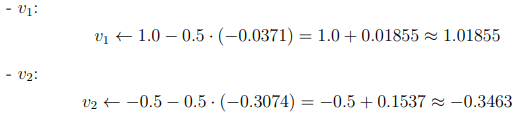
作业3

第一题

我们有一个四个单词的句子。对应的词嵌入a1、a2、a3和a4如下图所示：

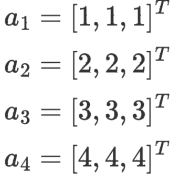
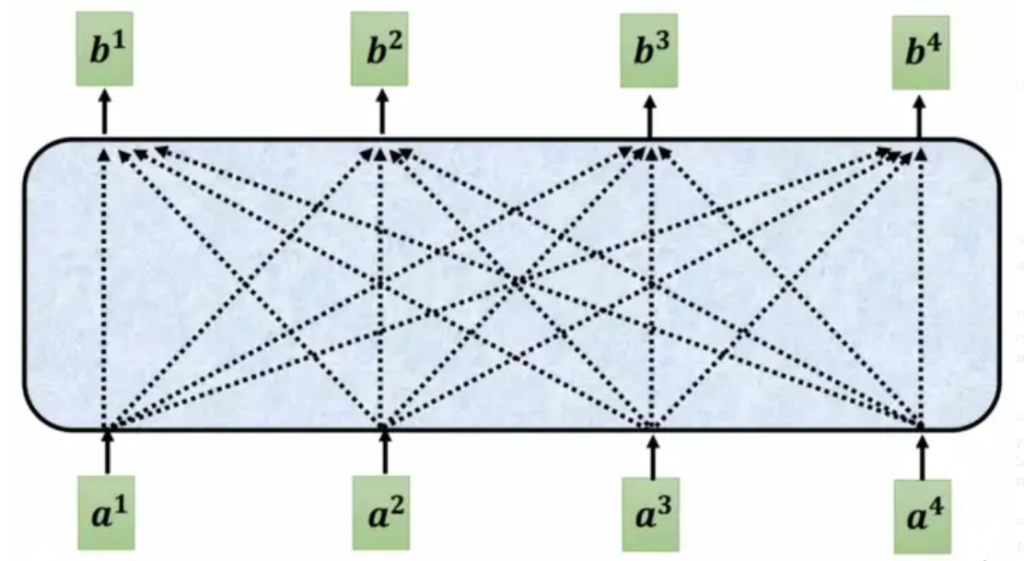
现在我们使用一个简单的自我关注层来处理这些输入，请计算第一个单词的新隐藏状态b1。（假设所有的模型需要的参数已初始化为1）

自注意力

第一步：H=WX
第二步：Q=WqH；K=WkH；V=WvH
第三步：$ A=\frac{KTQ}{\sqrt{d}} $ ; A’=softmax(A)注意这里一定要除$ \sqrt{d} $，d为q和k的维度
第四步：H’=VA’

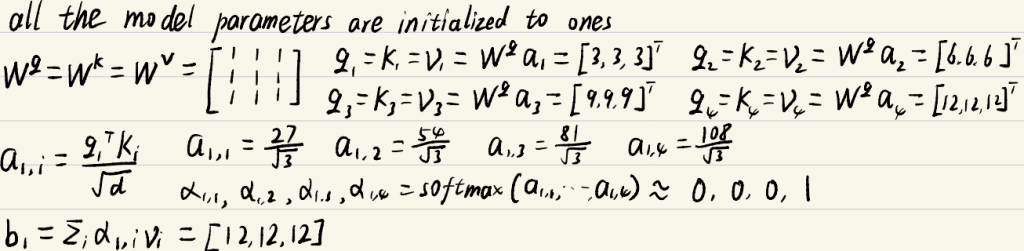
第二题

下面是一个小型卷积神经网络的示意图，它将13×13图像转换为4个输出值。该网络从输入到输出有以下层/操作：3个过滤器的卷积、最大池化、ReLU，最后是一个完全连接的层。对于这个网络，我们将不使用任何偏置/偏移参数（w0）。

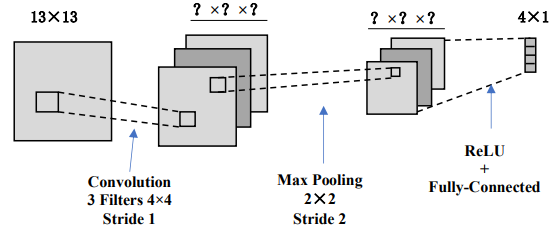
每层后图像/特征图的大小是多少？
我们需要学习卷积层中的多少权重？

卷积层有 3 个过滤器，每个过滤器的大小是 4×4。输入图像只有 1 个通道，则每个过滤器有 4×4=16 个权重。

总的卷积权重数为：
总权重=过滤器数×过滤器大小=3×16=48

卷积层中需要学习 48 个权重。

对正向传递执行了多少次 ReLU 操作？

ReLU 是逐元素操作，对每个特征图中的每个值执行一次。ReLU 层的输入是 3 个 5×5 的特征图，因此总共有：ReLU 操作数=3×5×5=75

正向传递中执行了 75 次 ReLU 操作

整个网络要学习多少权重

完全连接层的输出是 4 个值。每个输出值与输入所有 75 个值相连，因此完全连接层的权重数为：
完全连接层权重数=输入大小×输出大小=75×4=300

总权重数=卷积层权重数+完全连接层权重数=48+300=348

样卷

解答：

判断题

  • 错误
    • 逻辑回归是一种线性模型，适用于线性决策边界。当数据特征空间是非线性决策边界时，逻辑回归模型无法直接进行分类，通常需要通过特征转换或使用核方法来处理。
  • 正确
    • K-means的初始状态（初始质心的选择）会影响最终的聚类结果，因为K-means可能收敛到局部最优解。
  • 错误
    • 强化学习通过与环境交互获得奖励信号来学习策略，是一种有监督学习方法，不是无监督学习。
  • 正确
    • 增加神经网络的层数可以捕获更复杂的特征，因此具有更强的表征学习能力。
  • 正确
    • 池化层通过减少特征图的大小降低参数量，同时保留重要的特征。
  • 错误
    • 随机梯度下降收敛速度快，但它的更新方向有噪声，可能不稳定。批梯度下降更稳定，但速度较慢。

选择题

  1. ？
  2. C Adam优化算法引入了“动量”（momentum）概念。
  3. B 增加隐藏层神经元数量可能导致模型复杂度增加，从而加重过拟合。
  4. A 非线性分类问题可以通过特征转换（如核方法）转化为线性可分问题。
  5. C LSTM（长短期记忆网络）是处理序列预测任务的最佳选择，因为它能有效捕获长期依赖关系。
  6. C 每层卷积核大小为3×3，stride为1，不使用padding。三层网络的感受野大小为7×7。

简答题

  • 误差反向传播的角度谈LSTM相比RNN的优点
    LSTM通过引入记忆单元和门机制（输入门、遗忘门、输出门），解决了RNN中误差反向传播时梯度消失或梯度爆炸的问题。它能够通过记忆单元有效保存长期依赖信息，并通过门机制选择性地更新或遗忘信息，从而在长序列任务中表现优于传统RNN。
  • Self-Attention层的词向量本质区别
    第一层的词向量是基于初始词嵌入生成的，而最后一层的词向量通过多层Self-Attention机制提取了更高级的语义信息，能更好地表示词在整个上下文中的意义。

计算题

1.(a) 写出后验概率表达式
$ P(y|x_1, x_2, x_3) = \frac{P(y) \cdot P(x_1|y) \cdot P(x_2|y) \cdot P(x_3|y)}{P(x_1, x_2, x_3)} $

(b) 计算后验概率
表格数据

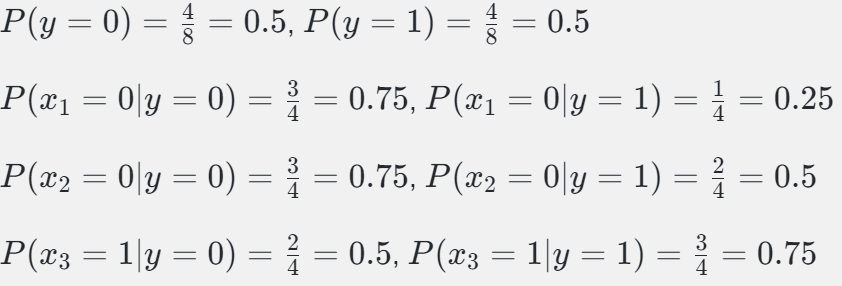
计算后验概率：
$ P(y=0|x_1=0, x_2=0, x_3=1) = \frac{P(y=0) \cdot P(x_1=0|y=0) \cdot P(x_2=0|y=0) \cdot P(x_3=1|y=0)}{P(x_1=0, x_2=0, x_3=1)} $
$ P(y=0|x_1=0, x_2=0, x_3=1) = \frac{0.5 \cdot 0.75 \cdot 0.75 \cdot 0.5}{Z} = \frac{0.140625}{Z} $
$ P(y=1|x_1=0, x_2=0, x_3=1) = \frac{P(y=1) \cdot P(x_1=0|y=1) \cdot P(x_2=0|y=1) \cdot P(x_3=1|y=1)}{P(x_1=0, x_2=0, x_3=1)} $
$ P(y=1|x_1=0, x_2=0, x_3=1) = \frac{0.5 \cdot 0.25 \cdot 0.5 \cdot 0.75}{Z} = \frac{0.046875}{Z} $

进过归一化，最后得到
$ P(y=0|x_1=0, x_2=0, x_3=1) = \frac{0.140625}{0.140625 + 0.046875} = 0.75 $
$ P(y=1|x_1=0, x_2=0, x_3=1) = \frac{0.046875}{0.140625 + 0.046875} = 0.25 $

所以预测y=0

2. 批梯度下降过程

数据点为 (1,3),(2,5),(3,7)，线性回归模型为 𝑦=𝑤⋅𝑥+𝑏。初始值为 𝑤=0,𝑏=0，学习率为 𝛼=0.1。

计算梯度：
$ \frac{\partial L}{\partial w} = -\frac{2}{3} \left[ (3 – (0 \cdot 1 + 0)) \cdot 1 + (5 – (0 \cdot 2 + 0)) \cdot 2 + (7 – (0 \cdot 3 + 0)) \cdot 3 \right] $
$ \frac{\partial L}{\partial w} = -\frac{2}{3} \left[ 3 \cdot 1 + 5 \cdot 2 + 7 \cdot 3 \right] = -\frac{2}{3} \cdot 38 = -25.33 $
$ \frac{\partial L}{\partial b} = -\frac{2}{3} \left[ (3 – (0 \cdot 1 + 0)) + (5 – (0 \cdot 2 + 0)) + (7 – (0 \cdot 3 + 0)) \right] $
$ \frac{\partial L}{\partial b} = -\frac{2}{3} \cdot (3 + 5 + 7) = -\frac{2}{3} \cdot 15 = -10 $

更新参数
$ w_{\text{new}} = w_{\text{old}} – \alpha \cdot \frac{\partial L}{\partial w} = 0 – 0.1 \cdot (-25.33) = 2.533 $
$ b_{\text{new}} = b_{\text{old}} – \alpha \cdot \frac{\partial L}{\partial b} = 0 – 0.1 \cdot (-10) = 1 $

更新到w和b后，继续三次

系统设计题

1. 图书价格区间预测

(1) 价格区间预测：

  • 特征：标题、简介（文本向量化处理如 TF-IDF）、出版日期（时间特征）、定价。
  • 模型：使用分类模型（如逻辑回归、随机森林或神经网络）。
  • 训练：输入历史图书数据，标签为价格区间。
  • 预测：对新图书分类为低价、中价或高价。

(2) 定向书籍推荐：

  • 特征：用户的阅读序列作为输入。
  • 模型：使用序列模型（如 LSTM 或 Transformer）。
  • 训练：输入用户历史阅读序列，预测下一本书。
  • 推荐：输出概率最高的书籍作为推荐结果。

2. 自动驾驶设计

(1) 障碍物识别：

  • 数据收集：采集道路图像，标注障碍物。
  • 模型：使用 CNN（如 ResNet）进行图像分类。
  • 训练：将图像输入 CNN，输出障碍物类别。
  • 部署：实时预测障碍物。

(2) 强化学习控制系统：

  • 状态：车辆位置、速度、环境信息。
  • 动作：加速、减速、转向等。
  • 奖励：根据行驶安全性和效率设计奖励函数。
  • 使用 Q 学习或 PPO 算法优化策略以最大化奖励。
暂无评论

发送评论 编辑评论 


				

			

						

				

					

						

							

								
							

							
						

					

				

				

					

						

							

								
							

							
						

					

				

				

					

						

							

								
							

							
							
													

					

				

			

			
			

				

					
				

			

				

											

							
							
						

																

							
							
						

																

							
							
						

										
					
											
						

	

		
|´・ω・)ノ
ヾ(≧∇≦*)ゝ
(☆ω☆)
（╯‵□′）╯︵┴─┴
￣﹃￣
(/ω＼)
∠( ᐛ 」∠)＿
(๑•̀ㅁ•́ฅ)
→_→
୧(๑•̀⌄•́๑)૭
٩(ˊᗜˋ*)و
(ノ°ο°)ノ
(´இ皿இ｀)
⌇●﹏●⌇
(ฅ´ω`ฅ)
(╯°A°)╯︵○○○
φ(￣∇￣o)
ヾ(´･ ･｀｡)ノ"
( ง ᵒ̌皿ᵒ̌)ง⁼³₌₃
(ó﹏ò｡)
Σ(っ °Д °;)っ
( ,,´･ω･)ﾉ"(´っω･｀｡)
╮(╯▽╰)╭
o(*////▽////*)q
＞﹏＜
( ๑´•ω•) "(ㆆᴗㆆ)
😂
😀
😅
😊
🙂
🙃
😌
😍
😘
😜
😝
😏
😒
🙄
😳
😡
😔
😫
😱
😭
💩
👻
🙌
🖕
👍
👫
👬
👭
🌚
🌝
🙈
💊
😶
🙏
🍦
🍉
😣
Source: github.com/k4yt3x/flowerhd
	

	

		
颜文字
Emoji
小恐龙
花!
	


									

			

			
			
		

	






上一篇
下一篇 

                    

                    
			        推荐文章
		            

		            

							
UE C++

							
							

							
数据挖掘及大数据分析

							
							

							
软件测试

							
							

							
游戏客户端技术栈+经验总结

							
							

							
Effective C++

							
							

							
操作系统

							
							

							
计算机图形学

							
							

							
C++知识点

							
							

							
计算机网络

							
							

							
力扣必刷题