题目都是hot100，记录做题心得。

两数之和

给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出 和为目标值 target  的那 两个 整数，并返回它们的数组下标。
你可以假设每种输入只会对应一个答案，并且你不能使用两次相同的元素。
你可以按任意顺序返回答案。

显而易见暴力方法，双层循环。有一些优化的点，比如最大数超过target就去掉，不过不影响复杂度。

vector<int> twoSum(vector<int>& nums, int target) {
        vector<int> v;
        for(int i = 0 ; i < nums.size() - 1 ; i++){
            for(int j = i + 1 ; j < nums.size() ; j++){
                if(nums[i] + nums[j] == target){
                    v = { i , j};
                    return v;
                }
            }
        }
        return v;
    }

结果比较好的是哈希表，基本原理就是 对于每一个x，我们首先查询哈希表中是否存在target – x，然后将x插入到哈希表中，即可保证不会让x和自己匹配。

tip:map和unordered_map

map：底层红黑树

unorder_map：散列表

vector<int> twoSum(vector<int>& nums, int target) {
        //创建哈希表
        unordered_map<int, int> hashtable;
        for(int i = 0 ; i < nums.size() ; i++){
            // 返回值是第二个数，如果走到最后，则说明不存在
            auto it = hashtable.find(target - nums[i]);
            if(it != hashtable.end()){
                return {hashtable[target-nums[i]], i};
            }
            // 不存在加入散列表
            hashtable[nums[i]] = i;
        }
         // c++要求必须最后有返回
        return {};
    }

字母异位词分组

给你一个字符串数组，请你将 字母异位词 组合在一起。可以按任意顺序返回结果列表。字母异位词 是由重新排列源单词的所有字母得到的一个新单词。

思路大概有直接的哈希，先把字母都拆开按顺序排好。最后遍历一遍就是答案。重点大概记一下语法，比如 string排序sort(key.begin() , key.end()); emplace_back的用法。

vector<vector<string>> groupAnagrams(vector<string>& strs) {
        // key 是排好序的，后面是其它乱序的
        unordered_map<string , vector<string>> mp ;
        for (auto str :strs){
            string key = str;
            sort(key.begin() , key.end());
            // 如果 key 已经存在，emplace_back 会把 str 添加到与 key 对应的 vector<string> 中。
            // 如果 key 不存在，mp[key] 会自动创建一个新的空 vector<string>，并将 str 添加进去。
            mp[key].emplace_back(str);
        }

        vector<vector<string>> answer;
        for(auto it = mp.begin() ; it != mp.end() ; it++){
            answer.emplace_back(it->second);
        }

        return answer;
    }

最长连续序列

给定一个未排序的整数数组 nums ，找出数字连续的最长序列（不要求序列元素在原数组中连续）的长度。请你设计并实现时间复杂度为 O(n) 的算法解决此问题。

显而易见，排序o（logn），这条路已经堵死了

class Solution {
public:
    int longestConsecutive(vector<int>& nums) {
        int max_len = 0;
        int length = nums.size();
        unordered_map<int , int> mp;
        for(int i = 0 ; i < length ; i++){
            mp[nums[i]] = i;
        }

        for(int i = 0 ; i < length ; i++){
            int current_len = 0;
            int start = nums[i];
            // 找到最前面
            while(mp.find(start - 1) != mp.end()){
                start -= 1;
            }
            // 从最前面往后统计，看多长
            while(mp.find(start)!= mp.end()){
                start += 1;
                current_len += 1;
            }
            max_len = current_len > max_len ? current_len : max_len;
        }
        return max_len;
    }
};

then

    int longestConsecutive(vector<int>& nums) {
        int max_len = 0;
        unordered_map<int , int> mp;
        // 先把每一个元素都插入散列表，便于O(1)看是否存在
        for(int i = 0 ; i < nums.size() ; i++){
            mp[nums[i]] = i;
        }

        for(auto &num : nums){
            // 遍历一遍，如果后面没元素了，则说明对了。
            // 找到最前面
            if(mp.find(num + 1) == mp.end()){
                int current_len = 1;
                while(mp.find(num - current_len) != mp.end()){
                    current_len += 1;
                }
                max_len = current_len > max_len ? current_len : max_len;
            }
        }
        return max_len;
    }

上面我其实感觉已经很好了，但是散列表对于相同数据不会覆盖，而是链表一直往后走。这就导致很多浪费了，事实上上面也超时了。最佳还是要用unorder_set

int longestConsecutive(vector<int>& nums) {
        // 创建这个set
        unordered_set<int> num_set;
        for (const int& num : nums) {
            num_set.insert(num);
        } 
        int longestStreak = 0;

        for (const int& num : num_set) {
            // 如果是最后一个，从最后往前统计
            if(!num_set.count(num + 1)){
                int current_len = 1;
                while(num_set.count(num - current_len)){
                    current_len ++;
                }
                if(current_len > longestStreak) longestStreak = current_len;
            }
            }
        }
        return longestStreak;           
    }

总结：set和map区别貌似就是有没有键值对。这里不需要value，所以set好一些。
set插入用insert，找用find或者count。

移动零

给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。

void moveZeroes(vector<int>& nums) {
        int zero = 0;
        int not_zero = 1;
        int length = nums.size();
        
        //思路是，从前往后找
        while(not_zero < length){
            //如果可以交换就交换
            if(nums[not_zero] != 0 && nums[zero] == 0){
                int temp = nums[not_zero] ;
                nums[not_zero] = nums[zero];
                nums[zero] = temp;
            }
            //先找到第一个为0的
            if(nums[zero] != 0) zero++;
            //再在这个数后面找到第一个非0的
            if(nums[not_zero] == 0) not_zero++;
            if(zero >= not_zero) not_zero = zero;
        }
    }

官方的思路也挺好

注意到：左指针左边均为非零数；右指针左边直到左指针处均为零。

大概就是右指针一直向右转，找到下一个不为0的数。左指针会在0处停下。

void moveZeroes(vector<int>& nums) {
        int n = nums.size(), left = 0, right = 0;
        //右指针不断向右移动，每次右指针指向非零数，则将左右指针对应的数交换，同时左指针右移。
        while (right < n) {
            if (nums[right]) {
                swap(nums[left], nums[right]);
                left++;
            }
            right++;
        }
    }

盛最多水的容器

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。

每次都从左右挑一个高度小的，因为只有最小的那一边变大，整体容量才可能变大。标准解答貌似每次都会计算容量，不过我的解法虽然不用这样却很长。综合考虑就这样吧。

int maxArea(vector<int>& height) {
        int l = 0, r = height.size() - 1;
        int ans = 0;
        while (l < r) {
            int area = min(height[l], height[r]) * (r - l);
            ans = max(ans, area);
            if (height[l] <= height[r]) {
                ++l;
            }
            else {
                --r;
            }
        }
        return ans;

三数之和

给你一个整数数组 nums ，判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ，同时还满足 nums[i] + nums[j] + nums[k] == 0 。请你返回所有和为 0 且不重复的三元组。

遍历O(N³)，很可惜就超时了

vector<vector<int>> threeSum(vector<int>& nums) {
        vector<vector<int>> ret;
        set<vector<int>> result;
        int length =  nums.size();

        for(int i = 0 ; i < length ; i++){
            for(int j = i + 1 ; j < length ; j++){
                for(int k = j + 1 ; k < length ; k++){
                    if (nums[i] + nums[j] + nums[k] == 0)
                    {
                        vector<int> temp = {nums[i] , nums[j] , nums[k]};
                        sort(temp.begin() , temp.end());
                        result.insert(temp);
                    }
                }
            }
        }
        for(auto key : result){
            ret.push_back(key);
        }
        return ret;
    }

双指针遍历，很巧妙

class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        int n = nums.size();
        vector<vector<int>> ret;
        sort(nums.begin() , nums.end());

        // 最左边指针
        for(int frist = 0 ; frist < n ; frist++){
            // 找到不一样的值
            if(frist > 0 && nums[frist -1] == nums[frist])
                continue;
            
            // third初始是最大的值
            int third = n -1;

            // 在中间遍历
            for(int second = frist + 1 ; second < third ; second++){
                if(second > frist + 1 && nums[second] == nums[second - 1] )
                    continue;
                
                //最小的两个相加都比最大值大，那需要最大值变小
                while(second < third && nums[second] + nums[third] + nums[frist] > 0){
                    third --;
                }

                //重合，可以退出了
                if(second == third) break;
                if(nums[second] + nums[third] + nums[frist] == 0){
                    ret.push_back({nums[frist], nums[second], nums[third]});
                }
            }
        }
        return ret;
    }
};

接雨水

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

初看非常逆天难，但是看了解析好像就又简单了

一是动态规划，二是下面的

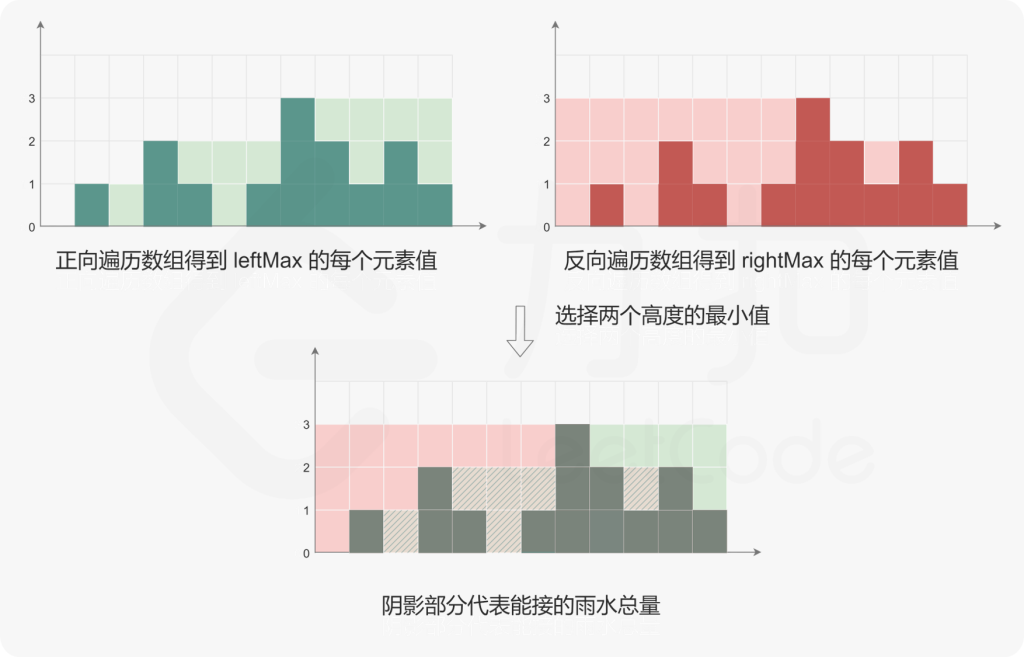
• 使用height[left]和height[right]的值更新leftMax和rightMax的值；
• 如果height[left]<height[right]，则必有leftMax<rightMax，下标left处能接的雨水量等于leftMax−height[left]，将下标left处能接的雨水量加到能接的雨水总量，然后将left加1（即向右移动一位）；
• 如果height[left]≥height[right]，则必有leftMax≥rightMax，下标right处能接的雨水量等于rightMax−height[right]，将下标right处能接的雨水量加到能接的雨水总量，然后将right减1（即向左移动一位）。

int trap(vector<int>& height) {
        int ans = 0;
        int left = 0 , right = height.size() - 1;
        int left_max = 0 , right_max = 0;

        while(left < right){
            //取当前最大
            left_max = max(left_max , height[left]);
            right_max = max(right_max , height[right]);
            
            //如果左边高度小于右边，表示左边一定可以都上
            if(height[left] < height[right]){
                ans += left_max - height[left];
                ++left;
            } else {
                ans += right_max - height[right];
                -- right;
            }
        }
        return ans;
    }

有一个更好理解的

和为 K 的子数组

给你一个整数数组 nums 和一个整数 k ，请你统计并返回 该数组中和为 k 的子数组的个数 。下面是一个单纯的排表，O（n²）

int subarraySum(vector<int>& nums, int k) {
      
        int sum = 0;
        int n = nums.size();
        
        for(int i = 0 ; i < n ; i++){
            int current = 0;
            for(int j = i ; j < n ; j++){
                current += nums[j];
                if(current == k) sum ++;
            }
        }
        return sum;
    }

结果答案有个甜菜想法，假设用a[i]表示从0加到i，那我要i,j之间只需要a[j] – a[i-1]。那这样，我要求一个区间[j,i]的和为target，则为a[i] – a[j] = target，那对于任意一个a[i]，我们只需要对它前面的数字判断，是否有等于a[i]-target即可，如果o1可以判断，那么最终算法复杂度就是O(n)

世界上想出这么巧妙算法的人都是甜菜吗？

int subarraySum(vector<int>& nums, int k) {
        unordered_map<int , int> mp;
        //保证比如说自相等情况下，可以统计到
        mp[0] = 1;
        int sum = 0;
        int count = 0;
        for(int i = 0 ; i < nums.size() ; i++){
            sum += nums[i];
            if(mp.find(sum - k) != mp.end()){
                count += mp[sum - k];
            }
            mp[sum]++;
        }
        return count;
        
    }

无重复字符的最长子串

给定一个字符串 s ，请你找出其中不含有重复字符的 最长 子串 的长度。

早上可能状态好？一下就做出来了
右指针每次都是新加入的元素，如果已经存在，那左指针就删掉自己的向右移动

int lengthOfLongestSubstring(string s) {
        unordered_set<char> st;
        int n = s.length();
        int left= 0 , right = 0;
        int max_length = 0;
        int current_length = 0;
        while(right < n ){
            //没找到
            if(st.count(s[right]) == 0){
                st.insert(s[right]);
                current_length ++;
                right++;
            }
            //找到了
            else{
                 st.erase(s[left]);
                 left++;
                 current_length --;
            }
            max_length = current_length > max_length ? current_length : max_length;
        }
        return max_length;
    }

找到字符串中所有字母异位词

给定两个字符串 s 和 p，找到 s 中所有 p 的 异位词 的子串，返回这些子串的起始索引。不考虑答案输出的顺序。

太低效了，直接timeout。复杂度是o(nNlogN)。看来必然是p后续的N太大了。

    vector<int> findAnagrams(string s, string p) {
        vector<int> ans;
        int n_s = s.length() , n_p = p.length();
        sort(p.begin() , p.end());
        int left = 0 ;
        while(left + n_p - 1 < n_s){
            string subStr = s.substr(left , n_p);
            sort(subStr.begin() , subStr.end());
            if(p == subStr){
                ans.push_back(left);
            }
            left++;
        }
        return ans;
    }

想出来了O（n）的，觉得非常够用。注意的点是，虽然unordered_map<char , int>在初始化时候，如果value没有，那默认是0，但是二者比较时候并不会相等。
剩下的就是滑动比较，加一个减一个

vector<int> findAnagrams(string s, string p) {
        vector<int> ans;
        int n_s = s.length() , n_p = p.length();
        unordered_map<char , int> mp;
        unordered_map<char , int> ans_mp;
        for(int i = 0 ; i < 26 ; i++){
            mp['a'+ i] = 0;
            ans_mp['a'+ i]  = 0;
        }

        for(int i = 0 ; i < n_p ; i++){
            mp[s[i]]++;
            ans_mp[p[i]]++;
        }
        for(int i = 0 ; i + n_p - 1 < n_s ; i++){
            if(mp == ans_mp){
                ans.push_back(i);
            }
            mp[ s[i] ]--;
            mp[ s[i + n_p] ]++;
        }
        return ans;
    }

滑动窗口最大值

给你一个整数数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。

返回 滑动窗口中的最大值 。

直接想到的方法是优先级队列。这样每次logN，整体就是nlogN。基于红黑树差不多

vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        // deque从前后都可以pop
        deque<int> q;
        int n = nums.size();

        // 先是对最前面K个，且题目提到 k < n了
        for(int i = 0 ; i < k ; i++){
            // 此时q内部是降序排列，如果后面的比他大，那说明前面的都没用了
            while(!q.empty() && nums[i] > nums[q.back()]){
                q.pop_back();
            }
            q.push_back(i);
        }

        //此时，第一个数字就是前面最大的
        vector<int> ans = {nums[q.front()]};
        for(int i = k ; i < n ; i++){
            //还是一样，如果大了就踢出去
            while(!q.empty() && nums[i] > nums[q.back()]){
                q.pop_back();
            }
            //极端情况可能有k+1个数，但无所谓，马上就踢人
            q.push_back(i);

            if(q.front() <= i - k){
                q.pop_front();
            }
            ans.push_back(nums[q.front()]);
        }
        return ans;

最小覆盖子串

给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串，则返回空字符串 "" 。

核心思想：右边r一直往右走，检查区间内是否满足要求。如果满足要求就缩左边，最终取到一个比较好的结果。

class Solution {
public:
    unordered_map<char , int> m_s;
    int check(){
        for(auto p : m_s){
            if(p.second < 0)
                return 0;
        }
        return 1;
    }

    string minWindow(string s, string t) {
        
        int n_s = s.length() , n_t = t.length();

        // 设定为负数，只有全正才说明满足要求
        for(int i = 0 ; i < n_t ; i++){
            m_s[t[i]] --;
        }

        int l = 0 , r = 0;
        int len = INT_MAX, ansL = -1;
        while(r < n_s){
            //对应的表里+1，向右移动
            m_s[s[r]]++;
 
            //当满足要求，开始缩左边
            while(check()){
                //比最大的小，更新左边答案
                if(r - l + 1 < len){
                    len = r - l + 1;
                    ansL = l;
                }
                m_s[s[l]]--;
                l++;
            }
            r++;
        }

        return ansL == -1 ? "" : s.substr(ansL , len);
    }
};

最大子数组和

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组是数组中的一个连续部分。

int maxSubArray(vector<int>& nums) {
        int  pre = 0 , max_ans = nums[0];
        for(int i = 0 ; i < nums.size() ; i++){
            // 当前数最大值，比较前面的数加上自己和当前数比较
            // 如果从自己这里开始好那前面的肯定没用了
            pre = max(pre + nums[i] , nums[i]);
            max_ans = max(max_ans , pre);
        }
        return max_ans;
    }

合并区间

以数组 intervals 表示若干个区间的集合，其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间，并返回 一个不重叠的区间数组，该数组需恰好覆盖输入中的所有区间 。

思路大概就是先排序，按照第一个数排。拍好后从前往后遍历处理。
没想到的点是sort(intervals.begin(), intervals.end());居然可以直接对二维数组排序，依据还是根据第一个数。

vector<vector<int>> merge(vector<vector<int>>& intervals) {
        if(intervals.size() == 0) return{};

        sort(intervals.begin(), intervals.end());
        int n = intervals.size();

        vector<vector<int>> ans;
        int l = intervals[0][0] , r = intervals[0][1];
        for(int i = 1 ; i < n ; i++){
            //左边都超出边界，则可以把之前那个加进去了，并开始新一轮循环
            if(intervals[i][0] > r){
                ans.push_back({l,r});
                l = intervals[i][0];
                r = intervals[i][1];
            }
            else{
                //扩宽到目前可达最远
                if(intervals[i][1] > r){
                    r = intervals[i][1];
                }
            }
        }
        //最后一对没有加上，补全
        ans.push_back({l,r});
        return ans;
    }

轮转数组

给定一个整数数组 nums，将数组中的元素向右轮转 k 个位置，其中 k 是非负数。

经典三次reverse，多想一下就感受到巧妙了

class Solution {
public:
    void reverse(vector<int>& nums , int start , int end){
        while(start < end){
            swap(nums[start] , nums[end]);
            start++;
            end--;
        }
    }
    void rotate(vector<int>& nums, int k) {
        int n = nums.size();
        k %= n;
        reverse(nums , 0 , n - 1);
        reverse(nums , 0 , k - 1);
        reverse(nums , k , n - 1);
    }
};

除自身以外数组的乘积

给你一个整数数组 nums，返回 数组 answer ，其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。

题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在  32 位 整数范围内。

请 不要使用除法，且在 O(n) 时间复杂度内完成此题。

一个classic思路，两个数组，一个记录正向乘积，另一个记录反向乘积。最终二者相结合，得到想要的答案

vector<int> productExceptSelf(vector<int>& nums) {
        int n = nums.size();
        vector<int> L(n , 0);
        vector<int> R(n , 0);

        L[0] = nums[0];
        R[n - 1] = nums[n - 1];
        for(int i = 1 ; i < n ; i++){
            L[i] = L[i -1] * nums[i];
            R[n - i - 1] = R [n - i] * nums[n - i - 1];
        }

        vector<int> ans(n , 0);
        ans[0] = R[1];
        ans[n - 1] = L[n-2];
        for(int i = 1 ; i < n - 1 ; i++){
            ans[i] = L[i - 1] * R[i + 1];
        }
        return ans;
    }

结果速度还不是很快。看的最佳的思路是，其实只用一个数组就够了。开始全部设置为1，左右双指针走。左指针就记录到这个位置左边乘积，乘好后放在这里。右边同理。这样一次就全部跑完了。甜菜还是太无法战胜了。

    vector<int> productExceptSelf(vector<int>& nums) {
        int n = nums.size();
        vector<int> ans(n , 1);
        int L = 1 , R = 1;
        for(int i = 1 ; i < n ; i++){
            L *= nums[i-1];
            ans[i] *= L;
            R *= nums[n - i];
            ans[n-i-1] *= R; 
        }
        return ans;
    }

只出现一次的数字

给你一个 非空 整数数组 nums ，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。

你必须设计并实现线性时间复杂度的算法来解决此问题，且该算法只使用常量额外空间。

非常经典的脑筋急转弯。开始想到的哈希表，结果就浪费O（n）空间不可以。。结果直接全部异或就完事了,,,还是挺无语的

缺失的第一个正数

给你一个未排序的整数数组 nums ，请你找出其中没有出现的最小的正整数。请你实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案。

int firstMissingPositive(vector<int>& nums) {
        // 这种也是神人题目了，或者说绝大部分困难题目
        // 无异于一个脑筋急转弯。看过就会，没看过就很可能想不出来。
        // 当你费劲心思想到一个解，却发现复杂度早就限制死了，接着看到答案只能无语的笑了

        int n = nums.size();
        //对于负数和0，全部让它超过数组大小，这样不会影响正常值
        for(int i = 0 ; i < n ; i++){
            if(nums[i] <= 0) nums[i] = n + 1;
        }

        // 那么剩下的就全是正数了，此时对于<= n的部分，去数组找对应位置，设置为负数(直接*-1那么偶数次会出问题)
        for(int i = 0 ; i < n ;i++){
            if(abs(nums[i]) <= n) nums[abs(nums[i]) - 1] = -abs(nums[abs(nums[i]) - 1]);
        }
        // 找到第一个正数即可，没有被映射过。
        for(int i = 0 ; i < n ; i++){
            if(nums[i] > 0 ) return i + 1; 
        }
        return n + 1;
    }

矩阵置零

给定一个 m x n 的矩阵，如果一个元素为 0 ，则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。

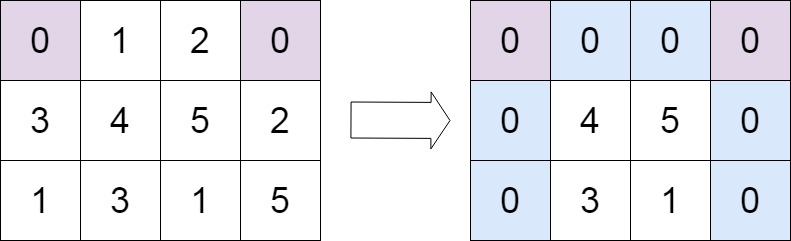
随手写的，时间复杂度O(MN)，一看100%那行了不优化了。

void setZeroes(vector<vector<int>>& matrix) {
        //考虑到这个unordered_set是O(1)查询，一定程度上也节省空间
        unordered_set<int> rows;
        unordered_set<int> cols;

        // 行数列数做好
        int row_size = matrix.size();
        int col_size = matrix[0].size();

        // 把为0的行数列数加进去
        for(int i = 0 ; i < row_size ; i++){
            for(int j = 0 ; j < col_size ; j++){
                if(matrix[i][j] == 0){
                    rows.insert(i);
                    cols.insert(j);
                }
            }
        }
        // 如果行数或者列数在set里，那就设置为0
        for(int i = 0 ; i < row_size ; i++){
            for(int j = 0 ; j < col_size ; j++){
                if(rows.count(i) || cols.count(j)){
                    matrix[i][j] = 0 ;
                }
            }
        }
    }

螺旋矩阵

给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。

旋转倒不是问题，开始我没想到怎么停下来。最后一想直接循环mn就行，，简单薄纱

vector<int> spiralOrder(vector<vector<int>>& matrix) {
        
        int row = matrix.size() , col = matrix[0].size();
        int i = 0 , j = 0; 
        int direction = 0 , circle = 0; //1,2,3,4表示四个方向，circle表示转了多少圈
        vector<int> ans;
        //一般情况下右转，但是如果是竖条，那么方向要向下
        if(col == 1) direction = 1;
        // 下面是有点屎的，理论上可以合并一块，不过懒得想了233333
        for(int k = 0 ; k < row * col ; k++)
        {
            ans.push_back(matrix[i][j]);
            if(direction == 0){
                j ++;
                //抵达边界，掉头
                if(j + circle >= col - 1)
                    direction++;
            } else if(direction == 1){
                i ++;
                if(i + circle >= row -1)
                    direction++;
            } else if(direction == 2){
                j --;
                if(j <= circle)
                {
                    direction++;
                }
            } else if(direction == 3){
                i--;
                if(i <= circle + 1)
                {
                    direction = 0;
                    circle++;
                }
            }
        }
        return ans;
    }

旋转图像

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

数学题，没意思。先行反转，再对角线。就100%AC了

void rotate(vector<vector<int>>& matrix) {
        //先行反转，再对角线
        int n = matrix.size();
        for(int i = 0 ; i < n /2 ; i++){
            swap(matrix[i] , matrix[n - 1 - i]);
        }
        for(int i = 0 ; i < n ; i++){
            for(int j = i + 1 ; j < n ; j++){
                swap(matrix[i][j] , matrix[j][i]);
            }
        }
    }

搜索二维矩阵 II

编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

每行的元素从左到右升序排列。每列的元素从上到下升序排列。

脑筋急转弯，看过就会。。

    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        // 右上角开始是二叉搜索树...
        int m = matrix.size() , n = matrix[0].size();
        int i = 0 , j = n - 1;
        while(i >= 0 && i < m && j >= 0 && j <n){
            if(target > matrix[i][j]){
                i++;
            }else if(target < matrix[i][j]){
                j--;
            }else {
                return true;
            }
        }
        return false;
    }

相交链表

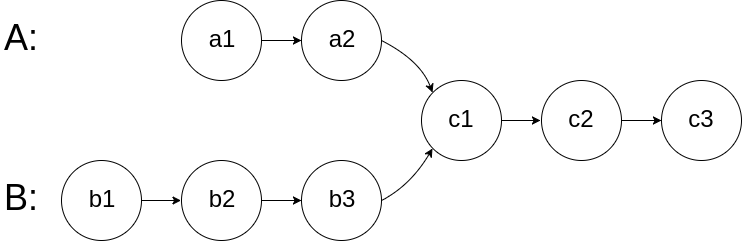
也是很经典了，和公共尾串思路一致。

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        ListNode *A = headA;
        ListNode *B = headB;

        int back = 0;
        while(back < 3 ){
            if(headA == headB) return headA;
            if(headA->next) headA = headA->next;
                else {
                    headA = B;
                    back++;
                }
            if(headB->next)headB = headB->next;
                else {
                    headB = A;
                    back++;
                }
        }
        return NULL;
    }
};

反转链表

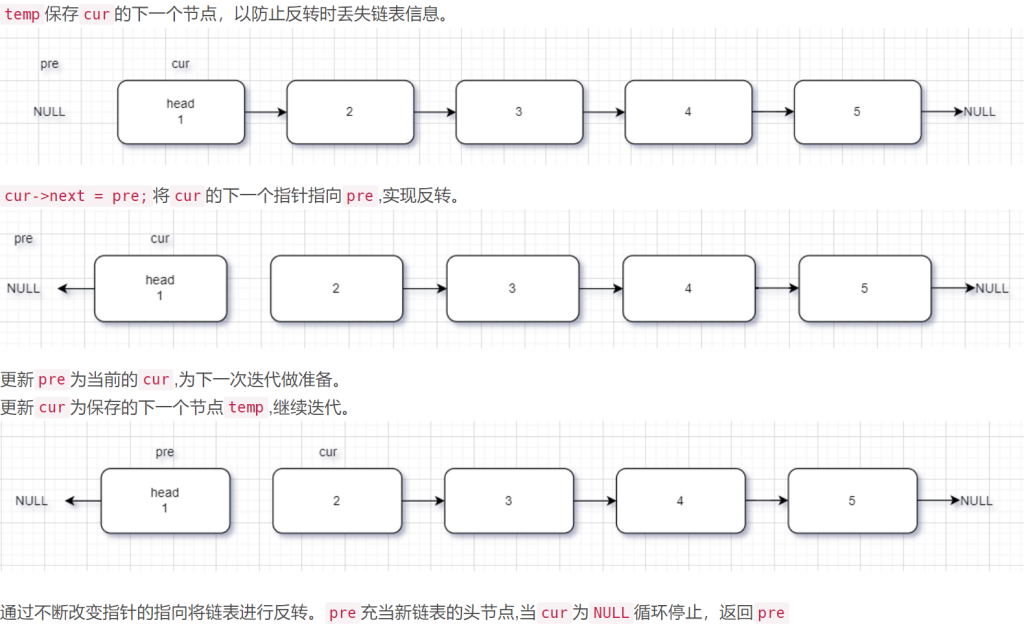
当初可没那么会，都要沉思很久，现在居然一下就写出来了

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        ListNode *cur , *temp , * pre = nullptr;
        cur = head;
        while(cur != nullptr){
            temp = cur->next; // temp的目的是因为cur掉头找不到下一个，因此提前锁定
            cur->next = pre; // pre目的是单向链表找不到前一个
            pre = cur;
            cur = temp;
        }
        return pre;
    }
};

回文链表

给你一个单链表的头节点 head ，请你判断该链表是否为回文链表。如果是，返回 true ；否则，返回 false 。

快慢指针找中间，翻转后续就都是顺序了。比较即可

class Solution {
public:
    ListNode* reverse(ListNode* head){
        ListNode *cur , *temp , *pre = nullptr;
        cur = head;
        while(cur){
            temp = cur->next;
            cur->next = pre;
            pre = cur;
            cur = temp;
        }
        return pre;
    }
    bool isPalindrome(ListNode* head) {
        // O(n)空间那就太简单了，但是O(1)
        // 快慢指针找中间，反转后续比较
        ListNode *fast = head, * slow = head;
        
        //先找到翻转点
        // 保证slow在需要翻转的前一个（无论奇偶）
        while(1){
            if(fast->next) {
                fast = fast->next;
            } 
            if(fast->next){
                fast = fast->next;
                slow = slow->next;
            } else{
                break;
            }
        }

        //现在翻转,比较每一个，直到最后
        ListNode* end = reverse(slow->next) ,* start = head;
        while(end){ //用后面这个是因为他短
            if(end->val != start->val) return false;
            end = end->next;
            start = start->next;
        }
        return true;
    }
};

环形链表

给你一个链表的头节点 head ，判断链表中是否有环

一眼丁真，快慢指针，过。我很好奇为什么我只超过20%但复杂度最优，发现第一名原来是检测循环走了10000还在走就是有环。。。。。。逆天

    bool hasCycle(ListNode *head) {
        ListNode *fast = head , *slow = head;
        if(head == NULL || head->next ==NULL) return false;
        fast = head->next->next;
        slow = head->next;
        while(fast){
            if(fast == slow){
                return true;
            }
            fast = fast->next;
            if(fast == NULL) return false;
            fast = fast->next;
            slow = slow->next;
        }
        return false;
    }

环形链表 II

数学推到类型，想出来就会

ListNode *detectCycle(ListNode *head) {
        //快慢指针走，相遇之后在从头来一个指针，相遇点就是环的位置。
        ListNode *fast = head , *slow = head;
        if(head == NULL || head->next ==NULL) return NULL;
        fast = head->next->next;
        slow = head->next;
        while(fast){
            if(fast == slow){
                ListNode *start = head;
                while(start != slow){
                    start = start->next;
                    slow = slow->next;
                }
                return start;
            }
            fast = fast->next;
            if(fast == NULL) return NULL;
            fast = fast->next;
            slow = slow->next;
        }
        return NULL;
    }

合并两个有序链表

经典题，不赘述

    ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
        ListNode *mergeList = new ListNode();
        ListNode *head = mergeList;
        // 谁小谁下一个
        while(list1 && list2){
            if(list1->val < list2->val){
                mergeList->next = list1 ;
                list1 = list1->next;
            } else {
                mergeList->next = list2;
                list2 = list2->next;
            }
            mergeList = mergeList->next;
        }
        if(list1) mergeList->next = list1;
        else mergeList->next =list2;
        return head->next;
    }

两数相加

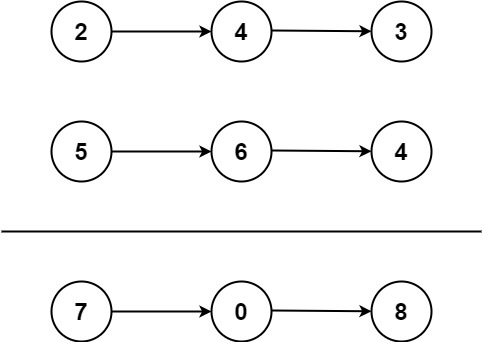
逆序数相加，如图是342 + 465 = 807.

有点啰嗦，但是100%AC，细节不优化了

    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
        ListNode* current_node = new ListNode();
        ListNode* head = current_node;
        int current = 0 , next = 0;
        //相加，存到一直节点。记录进位
        while(l1 && l2){
            int sum = l1->val + l2->val + next;
            current = sum % 10;
            next = sum / 10;
            l1->val = current;
            current_node->next = l1;
            current_node = current_node->next;

            l1 = l1->next;
            l2 = l2->next;
        }
        // 如果一边长一边短，那么还要接着算
        while(l1){
            int sum = l1->val + next;
            current = sum % 10;
            next = sum / 10;
            l1->val = current;
            current_node->next = l1;
            current_node = current_node->next;

            l1 = l1->next; 
            if(next == 0) break;
        }
        while(l2){
            int sum = l2->val + next;
            current = sum % 10;
            next = sum / 10;
            l2->val = current;
            current_node->next = l2;
            current_node = current_node->next;

            l2 = l2->next; 
            if(next == 0) break;
        }
        // 最后还进位，多加一个节点
        if(next == 1){
            ListNode* up = new ListNode(1);
            current_node->next = up;
            // new node
        }
        return head->next;

删除链表的倒数第 N 个结点

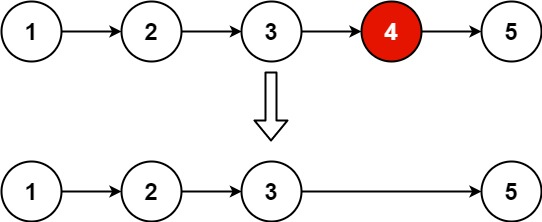
快慢指针秒了。一个指针快N个，那个到结尾这个就删

删除链表的倒数第 N 个结点

    ListNode* removeNthFromEnd(ListNode* head, int n) {
        ListNode* fast = head , *slow = head ;
        //保持领先N个，如果此时为空，则说明链表长度和要删的一样多，那么就去掉第一个就好
        while(n --) fast = fast->next;
        if(!fast) return head->next;
        //后面就是保持领先n+1个，这样方便删
        fast = fast->next;
        while(fast ) {
            fast = fast->next;
            slow = slow->next;
        }
        slow->next = slow->next->next;
        return head;
    }

两两交换链表中的节点

    ListNode* swapPairs(ListNode* head) {
        ListNode* start = new ListNode();
        // 辅助起点
        start->next = head;
        ListNode* left = start, * mid = head, *right = nullptr;
        
        //当前要交换俩节点为空
        while(mid && mid->next){
            //交换
            right = mid->next;
            mid->next = right->next;
            left->next=right;
            right->next = mid;

            //交换完成后调整
            left = mid;
            mid = mid->next;
        }

        return start->next;
    }

K 个一组翻转链表

题是不难，但是要注意边界情况。这里我整了很久，要注意几个点，比如开始的头节点不要往后跑了

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* reverse(ListNode* head){
        ListNode *pre = nullptr , * cur = head ,  *temp;
        while(cur){
            temp = cur->next;
            cur->next = pre;
            pre = cur;
            cur = temp;
        }
        return pre;
    }

    ListNode* reverseKGroup(ListNode* head, int k) {
        //一个简单的思路
        // 我要翻转一段，我就把这一段前后都断了，并记录头（尾会变成头不用管），和这一段前和后
        // 判断是否要翻转就排一个哨兵出去，能跑到指定位置不为空就能
        ListNode* hair = new ListNode();
        hair->next = head;

        ListNode* pre = hair , *A = head;
        ListNode* B = pre, * end = nullptr;


        while(1){
            for(int i = 0 ; i < k; i++) {
                B = B->next;
                if(!B) return hair->next;
            }
            end = B->next;

            B->next = nullptr;
            pre->next = reverse(A);
            A->next = end;

            pre = A ;
            A = end ;
            B = pre ;
        }
        return hair->next;
    }
};

随机链表的复制

意思就是，你拷贝一个node时候，里面的指针内容，你也要拷贝到新的里面。理解之后随便杀

Node* copyRandomList(Node* head) {
        unordered_map< Node* , Node*> mp;

        Node *start = head;
        Node *newList = new Node(0) ;
        Node *cur = newList;
        //先过一遍，哈希表对应上
        while(start){
            Node *node = new Node(start->val);
            cur->next = node;
            mp[start] = node;
            start = start->next;
            cur = cur->next;
        } 
        //再过一遍，找到random
        Node *newHead = newList->next;
        Node *oldList = head;
        while(newHead){
            newHead->random = mp[oldList->random];
            oldList = oldList->next;
            newHead = newHead->next;
        }
        return newList->next;
    }

排序链表

给你链表的头结点 head ，请将其按 升序 排列并返回 排序后的链表 。

mergesort，快慢指针找中点，然后归并

合并 K 个升序链表

俩俩合并，我这里用了队列很方便。注意是front，push，pop。没语法提示好累223333333

ListNode* mergeList(ListNode *a , ListNode *b){
        ListNode *head = new ListNode();
        ListNode *cur = head;
        while(a && b){
            if(a->val < b->val){
                cur->next = a;
                a = a->next;
            } else {
                cur->next = b;
                b = b->next;
            }
            cur = cur->next;
        }
        if(a) cur->next = a;
        else if(b) cur->next = b;
        return head->next;
    }
public:
    ListNode* mergeKLists(vector<ListNode*>& lists) {
        if(lists.size() == 0) return nullptr;
        queue<ListNode*> q;
        for(int i = 0 ; i < lists.size() ; i++){
            q.push(lists[i]);
        }
        while(q.size() >= 2){
            ListNode *node1 = q.front();
            q.pop();
            ListNode *node2 = q.front();
            q.pop();
            q.push(mergeList(node1 , node2));
        }
        return q.front();
    }

排序链表

时间复杂度符合要求，空间不符合。还有最后的合并链表居然写错了硬是发现不了。。。一长就会错真烦人。

class Solution {
public:
    ListNode* sortList(ListNode* head) {
        return devide(head);
    }
    ListNode *devide(ListNode* head){
        if(head == nullptr) return nullptr;
        if(head->next == nullptr) return head;
        cout << head->val << head->next->val;
        ListNode *fast = head,*slow = head;
        while(fast){
            fast = fast->next;
            if(fast) {
                fast = fast->next;
                if(fast) slow = slow->next;
            }
        } 
        ListNode *start = slow->next;
        slow->next = nullptr;

        ListNode *left = devide(head);
        ListNode *right = devide(start);
        return merge(left , right);
    }

    ListNode* merge(ListNode *L1 , ListNode *L2){
        ListNode *head = new ListNode();
        ListNode *temp = head;
        while(L1 && L2){
            if(L1->val < L2->val){
                temp->next = L1;
                L1 = L1->next;
            }else {
                temp->next = L2;
                L2 = L2->next;
            }
            temp = temp->next;
        }
        if(L1) temp->next = L1;
        else temp->next = L2;
        return head->next;
    }
};

LRU 缓存

优化了很多，感觉是符合要求了，但最后却还是超过很少的人…可能最好的方法就是不要用链表

class LRUCache {
struct Node{
    int key;
    int val ;
    Node *next = nullptr;
    Node *prev= nullptr;
    Node(){};
    Node(int key , int val):key(key),val(val){}
};

struct NodeList{
    unordered_map<int , Node*> mp;
    Node *head ;
    Node *tail ;
    int maxSize;
    int curSize;
    NodeList(){
        head = new Node();
        tail = head;
        curSize = 0;
    }

    int get(int key){
        // 哈希表，快速找
        if(!mp.count(key)) return -1;
        else{
            // 找到了，则需要返回目标值。相当于重新插入到队尾。
            int value = mp[key]->val;
            put(key , value);
            return value;
        }
    }

    void put(int key, int value) {
        // 先插入到队尾，如果超了就删除链表第一个
        // 哈希表，快速找，没找到直接加，找到了，删掉值再加
        Node *newNode = new Node(key , value);
        if(!mp.count(key)){
            tail->next = newNode;
            newNode->prev = tail;
            tail = tail->next;
            mp[key] = newNode;
        }
        else{
            // 找到了，删除后重新加入
            del(key);
            tail->next = newNode;
            newNode->prev = tail;
            tail = tail->next;
            mp[key] = newNode;
        }
        curSize ++;

        // 此时判断是否超出最大值，超过就删除第一个
        if(curSize > maxSize){
            del(head->next->key);
        }
    }

    void del(int key){
        // 这里在删之前都已经查找过确认存在
        // 维护双向指针
        Node *del = mp[key];
        Node *prev = del->prev;
        prev->next = del->next;
        if(del->next != nullptr) del->next->prev = prev;
        else {
            tail = tail->prev;
        }
        delete del;
        // 哈希表，删掉
        mp.erase(key);
        curSize --;
    }
};
NodeList *nodeList;
public:

    LRUCache(int capacity) {
        nodeList = new NodeList();
        nodeList->maxSize = capacity;
    }
    
    int get(int key) {
        return nodeList->get(key);
    }
    
    void put(int key, int value) {
        nodeList->put(key , value);
    }
};

/**
 * Your LRUCache object will be instantiated and called as such:
 * LRUCache* obj = new LRUCache(capacity);
 * int param_1 = obj->get(key);
 * obj->put(key,value);
 */

二叉树的中序遍历

经典。递归对于三种遍历都是只要改改位置就好了，为什么不都用递归呢（）

class Solution {
    vector<int> ans;
public:
    void inorder(TreeNode* root){
        if(!root) return;
        if(root->left != nullptr) inorder(root->left);
        ans.push_back(root->val);
        if(root->right != nullptr) inorder(root->right);
    };
    vector<int> inorderTraversal(TreeNode* root) {
        inorder(root);
        return ans;
    }
};

二叉树的最大深度

    int maxDepth(TreeNode* root) {
        if(root == nullptr ) return 0;
        else {
            return max (maxDepth(root->left) , maxDepth(root->right)) + 1;
        }
    }

翻转二叉树

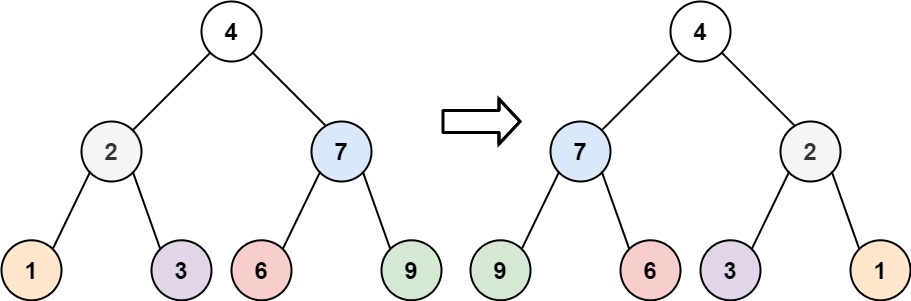
岁月静好，真好

class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if(root == nullptr) return nullptr;
        TreeNode *temp = root->right;
        root->right = invertTree(root->left);
        root->left = invertTree(temp);
        return root;
    }
};

对称二叉树

class Solution {
public:
    bool isSymmetric2(TreeNode* node1 , TreeNode* node2){
        if(node1 == nullptr || node2 == nullptr){
            if(node1 == nullptr && node2 == nullptr)
                return true;
            return false;
        } 

        if(node1->val != node2->val) return false;
        return isSymmetric2(node1->left , node2->right) && isSymmetric2(node1->right , node2->left);
    }
    bool isSymmetric(TreeNode* root) {
        if(root == nullptr) return true;
        return isSymmetric2(root->left , root->right);
    }
};

二叉树的直径

给你一棵二叉树的根节点，返回该树的 直径 。

二叉树的 直径 是指树中任意两个节点之间最长路径的 长度 。这条路径可能经过也可能不经过根节点 root 。

两节点之间路径的 长度 由它们之间边数表示。

重点是想明白，直径就是左子树高度+右子树高度。所以相当于遍历一遍后找到这个和最大的即可

class Solution {
    int ans = 0;
    int depth(TreeNode *t){
        if( t == nullptr) return 0;
        int L = depth(t->left);
        int R = depth(t->right);
        if(L + R > ans) ans = L + R;
        return max(L , R) + 1;
    }
public:
    int diameterOfBinaryTree(TreeNode* root) {
        depth(root);
        return ans ;
    }
};

二叉树的层序遍历

无需多言。但又一个深搜思路挺好的，你搜到那一层直接往后push就行了，而不是真的要层序遍历

    vector<vector<int>> levelOrder(TreeNode* root) {
        if(!root) return{};
        queue<TreeNode *>q;
        vector<vector<int>> v;
        q.push(root);
        int currentNum = 1 , nextNum = 0;
        vector<int> currentLevel;
        while(!q.empty()){
            TreeNode *cur = q.front();
            q.pop();
            currentLevel.push_back(cur->val);
            currentNum --;

            if(cur->left) {q.push(cur->left) ; nextNum++;};
            if(cur->right) {q.push(cur->right); nextNum++;};
            
            //下一层走完了
            if(currentNum == 0){
                currentNum = nextNum;
                nextNum = 0;
                v.push_back(currentLevel);
                currentLevel.clear();
            }
        }
        return v;
    }

验证二叉搜索树

即为检查中序遍历是否升序。如果用一个数组最后就O(n）了，不优雅。我才用的是一个变量，只要每遍历到一个后一个都比前一个大就行。这里要考虑INT_MIN问题，最开始我解决是再加了一个bool，判断是否出现两次INT_MIN即可

class Solution {
    int temp = INT_MIN;
    bool isBST = true , isMin = false;
public:
    void midTraversal(TreeNode* root){
        if(root == 0) return ;
        if(root->left) midTraversal(root->left);
        if(root->val <= temp){
            cout << "turn on";
            if((root->val == temp && temp == INT_MIN) && !isMin){
                isMin = true;
            }
            else isBST = false;
        }
        temp = root->val;
        if(root->right) midTraversal(root->right);
    }
    bool isValidBST(TreeNode* root) {
        midTraversal(root);
        return isBST;
    }
};

二叉搜索树中第 K 小的元素

这部还是中序遍历到第k个元素（？）秒了

class Solution {
public:
    int max_num , ans;
    void midTraverse(TreeNode* root){
        if(root == nullptr) return;
        if(root->left) midTraverse(root->left);
        if(--max_num == 0) ans = root->val;
        if(root->right) midTraverse(root->right);
    }
    int kthSmallest(TreeNode* root, int k) {
        max_num = k;
        midTraverse(root);
        return ans;
    }
};

二叉树的右视图

    void tailTraverse(TreeNode* root , int height){
        if(root == nullptr) return ;
        if(height > max_height) { ans.push_back(root->val); max_height++;};
        if(root->right) tailTraverse(root->right , height + 1);
        if(root->left) tailTraverse(root->left , height + 1);

    }
    vector<int> rightSideView(TreeNode* root) {
        // 后续遍历，每层遇到第一个加进去
        tailTraverse(root , 0);
        return ans;
    }

二叉树展开为链表

直接循环展开，但反正都是O(N)，那么直接开一个O(N)的表似乎也一样

    void flatten(TreeNode* root) {
        if(!root) return;
        TreeNode *head = new TreeNode();
        TreeNode *cur = head;

        stack<TreeNode *> s;
        s.push(root);
        while(!s.empty()){
            TreeNode *temp = s.top();
            s.pop();
            if(temp->right != nullptr) s.push(temp->right);
            if(temp->left != nullptr) s.push(temp->left);

            cur->right = temp;
            cur->left = nullptr;
            cur = cur->right;
        }
    }

从前序与中序遍历序列构造二叉树

开始一个n2了，估计是复制时候太浪费了。

TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        int n = inorder.size();
        if(n == 0) return nullptr;

        int mid = preorder[0];
        TreeNode *newNode = new TreeNode(mid);

        //找到中序遍历中的位置，停在相等那个位置
        int i = 0;
        while(inorder[i] != mid) i++;
        cout << i;
        if( i != 0 ){
            vector<int> leftPre(preorder.begin() + 1 , preorder.begin()+ i + 1);
            vector<int> leftIn(inorder.begin() , inorder.begin() + i );
            newNode->left = buildTree(leftPre , leftIn);
        }else{
            newNode->left == nullptr;
        }

        if (i != n - 1){
            vector<int> rightPre(preorder.begin() + i + 1 ,  preorder.end());
            vector<int> rightIn(inorder.begin() + i + 1 , inorder.end());
            newNode->right = buildTree(rightPre , rightIn);
        }else{
            newNode->right == nullptr;
        }
        return newNode;
    }

优化了一下,啊啊啊为什么还是N2复杂度，但确实快了不少

    TreeNode *buildT(vector<int>& preorder, vector<int>& inorder , int pl , int pr , int il , int ir){
        // 闭区间，右边小于左边则不存在
        if(pl > pr) return nullptr;

        // 根节点是前序遍历第一个
        int rootNum = preorder[pl];
        TreeNode *newNode = new TreeNode(rootNum);

        //中序遍历中，找到根节点位置
        int i = 0;
        while(inorder[il + i] != rootNum) i++;

        // 前序遍历，第一个是根节点，所以从第二个遍历到第i个节点
        // 中序遍历，从第一个到第i-1个位置
        newNode->left = buildT(preorder,inorder, pl + 1 , pl + i , il , il +i - 1 );

        // 后面都一样，从第i+1个到最后的位置
        newNode->right = buildT(preorder,inorder, pl + i + 1 , pr , il + i + 1 , ir);

        return newNode;

    }
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        int n = inorder.size();
        return buildT(preorder, inorder , 0 , n -1 ,0 , n -1);
    }

最后发现，问题是中序遍历，找到和前序遍历相同的时候，一个个查询太慢了。直接哈希映射解决hhhh。双on解决

class Solution {
    unordered_map<int , int> mp;
public:
    TreeNode *buildT(vector<int>& preorder, vector<int>& inorder , int pl , int pr , int il , int ir){
        // 闭区间，右边小于左边则不存在
        if(pl > pr) return nullptr;

        // 根节点是前序遍历第一个
        int rootNum = preorder[pl];
        TreeNode *newNode = new TreeNode(rootNum);

        // 快速找到差了多少
        int i = mp[rootNum] -il;

        // 前序遍历，第一个是根节点，所以从第二个遍历到第i个节点
        // 中序遍历，从第一个到第i-1个位置
        newNode->left = buildT(preorder,inorder, pl + 1 , pl + i , il , il +i - 1 );

        // 后面都一样，从第i+1个到最后的位置
        newNode->right = buildT(preorder,inorder, pl + i + 1 , pr , il + i + 1 , ir);

        return newNode;

    }
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        int n = inorder.size();
        for(int i = 0 ; i < n ; i++ ){
            mp[inorder[i]] = i;
        }
        return buildT(preorder, inorder , 0 , n -1 ,0 , n -1);
    }
};

路径总和 III

就是求区间和为一个值的数量一样的。深度优先搜索，把每一条路径都看出那个要求的数组即可。回来之后把节点排出，解决。重点还是数学推导，理解了这一步就特别好做。

class Solution {
public:
    unordered_map< long long , int > mp;
    int sum = 0;
    void dfs(TreeNode* root, long long  prefixSum , int targetSum){
        //unordered_map记录前缀和，如果找到有当前前缀和 - targetSum的，说明存在一个
        prefixSum += root->val;
        sum+= mp[prefixSum - targetSum];//有几个符合要求加几个
        mp[prefixSum] += 1;
        if(root->left) dfs(root->left , prefixSum , targetSum);
        if(root->right) dfs(root->right , prefixSum , targetSum);
        mp[prefixSum] -= 1;
    }
    int pathSum(TreeNode* root, int targetSum) {
        mp[0] = 1;
        if(!root) return 0;
        dfs(root , 0 , targetSum);
        return sum;
    }
};

二叉树的最近公共祖先

开始大概是想要记录路径，虽然是on但是特别慢。因为记录了整条路径

class Solution {
    unordered_map<TreeNode* , TreeNode*> mp_p;
    unordered_map<TreeNode* , TreeNode*> mp_q;
    int find_p = 0, find_q = 0;
    void dfs(TreeNode* root,TreeNode* p , TreeNode* q){
        if(!root) return ;
        if(root == p) find_p = 1;
        if(root == q) find_q = 1;
        if(root->left){
            if(!find_p)mp_p[root] = root->left;
            if(!find_q)mp_q[root] = root->left;
            dfs(root->left, p ,q ); 
        }
        if(root->right){
            if(!find_p)mp_p[root] = root->right;
            if(!find_q)mp_q[root] = root->right;
            dfs(root->right, p , q );
        }
    }
public:
    
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        // 只要dfs遍历到，记录路径，转化为双链表问题公共前缀
        if(root == NULL) return NULL;
        dfs(root, p , q);
        TreeNode *same = root;
        while(mp_p[same] == mp_q[same]){
            same = mp_p[same];
        }
        return same;
    }
};

答案就感觉是充分利用每一个条件的解一样，稍微一遍就不能用了。p!=q这个条件充分利用上了。不过虽然但是好像也没有好多少。

TreeNode* ans;
    bool dfs(TreeNode* root, TreeNode* p, TreeNode* q) {
        if (root == nullptr) return false;
        bool lson = dfs(root->left, p, q);
        bool rson = dfs(root->right, p, q);
        if ((lson && rson) || ((root->val == p->val || root->val == q->val) && (lson || rson))) {
            ans = root;
        } 
        return lson || rson || (root->val == p->val || root->val == q->val);
    }
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        dfs(root, p, q);
        return ans;
    }

二叉树中的最大路径和

class Solution {
    int maxNum = INT_MIN;
public:
    int calculate(TreeNode* root){
        // 计算当前最大值，即
        // dp[root] = max { dp[root->left] , dp[root->right]  , 0} + val
        // 对于每个root ,比较 dp[root->left] + dp[root->right] + val，取出那个值即可
        // 这里可以不用动归空间，因为需要的刚好计算了
        int left = 0 , right = 0;
        if(root->left) left = calculate(root->left);
        if(root->right) right = calculate(root->right);
        int ret = max(max(left , right),0);
        int cur_max = max(ret , left + right ) + root->val;
        maxNum = max(cur_max , maxNum);
        return ret + root->val;
    }
    int maxPathSum(TreeNode* root) {
        calculate(root);
        return maxNum;
    }
};

腐烂的橘子

dfs走一遍，每次检查。复杂度已经最优，具体懒得优化。

class Solution {
public:
    int m ;
    int n ;
    int isIllegal(int x ,int y){
        if(x >= 0 &&  x <= m-1 && y >=0 && y<= n-1) return true;
        return false;
    }
    int nextTime(vector<vector<int>>& grid){
        //先找出全部烂橘子
        vector<vector<int>> vec;

        for(int i = 0 ; i < m ; i ++){
            for(int j = 0 ; j < n ; j++){
                if(grid[i][j] == 2) vec.push_back({i,j});
            }
        }
        int flag = 0;// 1表示有更新，0表示没更新
        for(auto v :vec){
            int x = v[0]; //m
            int y = v[1]; //n
            if(isIllegal( x-1 , y) && grid[x-1][y] == 1){
                    grid[x-1][y] =2;
                    flag = 1;
            }
            if(isIllegal( x+1 , y) && grid[x+1][y] == 1){
                    grid[x+1][y] =2;
                    flag = 1;
            }
            if(isIllegal( x , y+1 ) && grid[x][y+1] == 1){
                    grid[x][y+1] =2;
                    flag = 1;
            }
            if(isIllegal( x , y-1 ) && grid[x][y-1] == 1){
                    grid[x][y-1] = 2;
                    flag = 1;
            }
        }
        if(flag == 0){
            for(int i = 0 ; i < m ; i ++){
                for(int j = 0 ; j < n ; j++){
                    if(grid[i][j] == 1) return -1;
                }
            }
        }
        return flag;
    }
    int orangesRotting(vector<vector<int>>& grid) {
        m = grid.size();
        n = grid[0].size();
        int times = 0;
        while(1) {
            int temp = nextTime(grid);
            // 1表示有更新
            if(temp == 1) times++;
            // -1不可能 
            else if(temp == -1) return -1;
            else return times;
        }
    }
};

课程表

本质就是考察图有没有环。那么找入度为0点，开始遍历。最后无法遍历时候，如果没有入度为0点却还是有边，则说明有环，不符合条件

class Solution {
public:
    bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
        vector<int> indegs(numCourses , 0);
        vector<vector<int>> edges(numCourses);
        for(auto v : prerequisites){
            //要学0，先要会1，也就是1指向0的边
            edges[v[1]].push_back(v[0]);
            //添加每天边的入度
            indegs[v[0]]++;
        }

        // 现在对于每一个入度为0的顶点，开始遍历
        queue<int> nodes;
        for(int i = 0 ; i < numCourses ;i++){
            if(indegs[i] == 0) {
                nodes.push(i);
            }
        }
        //开始从入度为0点开始遍历，如果没有入度为0点却还是有边，则说明有环，不符合条件
        while(nodes.size()){
            int node = nodes.front();
            nodes.pop();
            // 把它指的每一条边加进去，入度减少
            for(auto edge : edges[node]){
                if(--indegs[edge] == 0) nodes.push(edge);
            }
            numCourses--;
        }
        if(!numCourses) return true;
        return false;
        
    }
};

实现 Trie (前缀树)

一个节点一个字母…..

class Trie {

struct Node{
    vector<bool> chs;
    vector<Node *> nodes;
    int isEnd = 0;
    char selfCh ;

    Node(int isEnd = 0, char ch = ' '):isEnd(isEnd) , selfCh(ch){chs.resize(26 , false);}
    // 找特定结果的节点
    Node *searchNode(char ch){
        for(auto node : nodes){
            if(node->selfCh ==  ch){
                return node;
            }
        }
        return nullptr;
    }

    Node* pushNewNode( char ch){
        Node *node = new Node(0 , ch);
        nodes.push_back(node);
        return node;
    }
};

Node *head ;
public:

    Trie() {
        head = new Node();
    }
    
    void insert(string word) {
        int n = word.length();
        Node *start = head;
        // 遍历到最后一个
        for(int i = 0 ; i < n ; i++){
            //如果已经插入过了，去找这个节点
            if(start->chs[word[i] - 'a'] == true ){
                start = start->searchNode(word[i]);
            }
            // 没插入过，就插入并设置为true
            else{
                start->chs[word[i] - 'a'] = true;
                start = start->pushNewNode(word[i]);
            }
        }
        start->isEnd = 1;
    }
    
    bool search(string word) {
        Node *start = head;
        for(auto ch : word){
            if(start->chs[ch - 'a'] == true){
                start = start->searchNode(ch);
            } else{
                return false;
            }
        }
        return start->isEnd;
    }
    
    bool startsWith(string prefix) {
        Node *start = head;
        for(auto ch : prefix){
            if(start->chs[ch - 'a'] == true){
                start = start->searchNode(ch);
            } else{
                return false;
            }
        }
        return true;
    }
};

/**
 * Your Trie object will be instantiated and called as such:
 * Trie* obj = new Trie();
 * obj->insert(word);
 * bool param_2 = obj->search(word);
 * bool param_3 = obj->startsWith(prefix);
 */

岛屿数量

找到节点之后，就把它周边全部都变成0。清除这一边地。跳几次就是几个岛。不过有几个优化的点，一是pair很快，二是扫到周边是1直接让他为0，避免多次重复判断。

class Solution {
public:
    int m ;
    int n ;
    inline bool isIllegal(int x , int y){
        return (x >= 0 && x <= m -1 && y >= 0 && y <= n-1) ;
    }
    
    int numIslands(vector<vector<char>>& grid) {
        m = grid.size();
        n = grid[0].size();

        int islandNum = 0;
        for(int i = 0 ; i < m ; i++){
            for(int j = 0 ; j < n ; j++){
                if(grid[i][j] == '1'){
                    islandNum++;
                    //找到节点之后，就把它周边全部都变成0。清除这一边地
                    queue<pair<int,int>> q;
                    q.push({i,j});
                    grid[i][j]='0';
                    while(!q.empty()){
                        auto v = q.front();
                        q.pop();
                        int x = v.first , y = v.second;
                        if(isIllegal(x-1,y) && grid[x-1][y] == '1') {q.push({x-1,y}); grid[x-1][y] = '0';}
                        if(isIllegal(x+1,y) && grid[x+1][y] == '1') {q.push({x+1,y}); grid[x+1][y] = '0';}
                        if(isIllegal(x,y-1) && grid[x][y-1] == '1') {q.push({x,y-1}); grid[x][y-1] = '0';}
                        if(isIllegal(x,y+1) && grid[x][y+1] == '1') {q.push({x,y+1}); grid[x][y+1] = '0';}
                    }
                }
            }
        }
        return islandNum;
    }
};

回溯算法

不如动态规划，但有些动态规划还真不行。本质就是递归，递归的好就行。

全排列

这类算法貌似之前没学过，一点感觉都没有。但本质就是递归

class Solution {
public:
    
    vector<vector<int>> permute(vector<int>& nums) {
        int n = nums.size();
        int cur = 0;

        vector<vector<int>> ans;
        calculate(ans , nums , 0 , n);
        return ans;

    }
    // n是长度 cur是当前位
    void calculate(vector<vector<int>> &ans , vector<int> nums , int cur , int n){
        // 最后一位了，可以插入
        if(cur == n - 1) ans.push_back(nums);
        else{
            // 不是最后一位，依次交换
            for(int i = cur ; i < n; i++){
                swap(nums[i] , nums[cur]);
                calculate(ans , nums , cur + 1 , n);
                swap(nums[i] , nums[cur]);
            }
        }
    }
};

子集

一遍过的居然是这种模模糊糊的，晕晕的很神奇就过了

class Solution {
public:
    vector<vector<int>> subsets(vector<int>& nums) {
        vector<vector<int>> ans;
        vector<int> curs;
        int cur = 0 , n = nums.size();

        ans.push_back({});
        sub(ans , nums ,curs ,cur , n);
        return ans;
    }

    void sub(vector<vector<int>> &ans , vector<int> nums , vector<int> curs , int cur , int n ) {
        //从当前位置遍历
        for(int i = cur ; i < n ; i++){
            // curs维护目前集合，加入一个新数字
            curs.push_back(nums[i]);
            // 答案就新加一种
            ans.push_back(curs);
            // 接着向后遍历出全部
            sub(ans , nums , curs , i + 1 , n);
            // 可以排出来了，再插入其他数字。注意为了避免重复，只可以对这个数字后面的数字再操作。可以想象一下自己如何全排列一个数组，从第一个数开始，再从第二个数不往前。
            curs.pop_back();
        }
    }
};

电话号码的字母组合

貌似理解这个回溯的感觉就很好处理了。

class Solution {
public:
    unordered_map<char , string> mp;
    vector<string> letterCombinations(string digits) {
        if(digits == "") return {};
        mp['2'] = "abc";
        mp['3'] = "def";
        mp['4'] = "ghi";
        mp['5'] = "jkl";
        mp['6'] = "mno";
        mp['7'] = "pqrs";
        mp['8'] = "tuv";
        mp['9'] = "wxyz";

        vector<string> ans;
        string curs ;
        int cur = 0 , n = digits.length();
        dep(ans, curs , digits , cur , n);
        return ans;
    }

    void dep(vector<string> &ans , string curs , string &digits , int cur , int n){
        if(cur == n) ans.push_back(curs);
        else{
            for(auto ch : mp[digits[cur]]){
                curs.push_back(ch);
                dep(ans , curs , digits , cur + 1, n);
                curs.pop_back();
            }
        }
    }
};

组合总和

第一次错了。如果开始的数组不排序的话，那么出现 [2,3,3]和[3,2,2]之类情况发生，如果拍排好序顺着选就没问题了。数组最后是back，要记住（）（）

class Solution {
public:
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        vector<vector<int>> ans;
        int curSum = 0;
        vector<int> vec;
        sort(candidates.begin() , candidates.end());
        sub(candidates , ans , target , curSum , vec);
        return ans;
    }
    void sub(vector<int>& candidates, vector<vector<int>> &ans , int target , int curSum , vector<int> vec){
        // 超过最大，肯定不行
        if(curSum > target) return ;
        // 等于，则说明可以
        else if(curSum == target) ans.push_back(vec);
        else{
            // 顺着遍历每一个，必须不小于前一个数（用curSum为0代表第一次来的时候）
            for(auto can : candidates){
                if(curSum == 0 || can >= vec.back()){
                    vec.push_back(can);
                    sub(candidates , ans , target , curSum + can , vec);
                    vec.pop_back();
                }
            }
        }
    }
};

括号生成

c++里面等号不传递 :joker:，也就是说别想着a == b == c，，，其它的逻辑还是很显然的。中间判断逻辑有些冗余，但没事，这样比较容易读（））

class Solution {
public:
    vector<string> generateParenthesis(int n) {
        vector<string> ans;
        dep(ans , "" , 0 , 0 , n);
        return ans;
    }

    void dep(vector<string> & ans , string cur , int l , int r ,int n){
        if(l == r && l== n) ans.push_back(cur);
        else{
            // 如果左括号 = 右括号，则说明只能 加左括号.反之都可以
            if(l == r){
                cur.push_back('(');
                dep(ans , cur , l + 1, r, n);
                cur.pop_back();
            }
            else if(l < n ){
                cur.push_back('(');
                dep(ans , cur , l + 1, r, n);
                cur.pop_back();
                cur.push_back(')');
                dep(ans , cur , l, r + 1, n);
                cur.pop_back();
            }
            else{
                cur.push_back(')');
                dep(ans , cur , l, r + 1, n);
                cur.pop_back();
            }
        }
    }
};

单词搜索

多看几眼题2333，初始条件看错白忙活半天

class Solution {
public:
    vector<vector<bool>> mp;
    bool exist(vector<vector<char>>& board, string word) {
        // 对首字母深度优先遍历
        int x = board.size() , y = board[0].size(),lens = word.length();
        //初始化
        mp.resize(x);
        for(int i = 0 ; i < x ; i++) mp[i].resize(y , false);
        for(int i = 0 ; i < x ; i++){
            for(int j = 0 ; j < y ; j++){
                if(dfs(i , j , word , board , lens , x , y , 0 )){
                    return true;
                }
            }
        }
        return false;
    }
    bool dfs(int i , int j , string & word ,vector<vector<char>>& board, int lens , int x , int y , int depth){
        if(lens == depth) return true;
        else{
            if(i < 0 || j > y-1 || j < 0 || i > x-1) return false;
            if(mp[i][j]) return false;
            else if(word[depth] != board[i][j])  return false;
            else{
                mp[i][j] = true;
                bool ans = dfs(i+1,j,word,board,lens,x,y,depth+1) || dfs(i-1,j,word,board,lens,x,y,depth+1) 
                || dfs(i,j+1,word,board,lens,x,y,depth+1) || dfs(i,j-1,word,board,lens,x,y,depth+1) ;
                mp[i][j] = false;
                return ans;
            }
        }
    }
};

分割回文串

我这个小优化确实快了一点，看它分析复杂度从（2^n到n^2了，但是并没有快多少23333，看来还是数据量太少了）

class Solution {
public:
    vector<vector<int>> dp;
    vector<vector<string>> partition(string s) {
        // 先实现一个检测区间是否是回文的，用之前的动态规划，复杂度o(n2)，
        // 接着partition，依次往后。如果这个是回文区间，那就加进去（这里由于都算完了，检测o1就完成，不然很多重复计算）
        // 退出条件就是划分到最后面了
        vector<vector<string>> ans;
        vector<string> cur;
        int start = 0;
        int n = s.length();
        setDp(s, n);
        part(s , ans , cur , start , n);
        return ans;
    }
    void setDp(string s , int n){
        // dp[i][j] = dp[i+1][j-1] && s[i] == s[j]
        dp.resize(n);
        for(int i = 0 ; i < n ; i++) dp[i].resize(n);
        
        for(int j = 0 ; j < n ; j ++){
            for(int i = 0 ; i < n - j; i++){
                if(j == 0) dp[i][i+j] = 1;
                else if(j == 1) dp[i][i+j] = int(s[j+i] == s[i]);
                else {
                    dp[i][i+j] = dp[i+1][i+j-1] && int(s[i] == s[j+i]);
                }
            }
        }
    }

    int check(int start , int end , string &s){
        return dp[start][end];
    }
    void part(string s ,vector<vector<string>> &ans, vector<string> cur , int start , int n ){
        if(start == n) ans.push_back(cur);

        for(int i = start ; i < n ; i++){
            // 如果是回文，就插入递归后续
            if(check(start , i , s) == 1){
                string subStr(s.begin() + start , s.begin() + i + 1);
                cur.push_back(subStr);
                part(s , ans , cur , i + 1, n);
                cur.pop_back();
            }
        }
    }
};

N 皇后

大名鼎鼎，但是感觉并不难。都是一个复杂度量级，不知道我的为什么回慢这么多

class Solution {
public:
    vector<vector<int>> matrix;
    vector<vector<string>> solveNQueens(int n) {
        vector<string> v(n);
        for(int i = 0 ; i < n ; i++) v[i].resize(n,'.');
        vector<vector<string>> ans ;
        dep(0,n,0,0,v,ans);
        return ans;
    }
    
    bool isIllegal ( int x, int y){
        for(auto key : matrix){
            if( key[1] == y || abs(y - key[1]) == abs(x - key[0])){
                return false;
            }
        }
        return true;
    }
    void dep(int cur , int n  , int x, int y,  vector<string> &v , vector<vector<string>> &ans ){
        if(cur == n) ans.push_back(v);
        else{
            // 每次从下一行迭代
            for(int j = 0 ; j < n ; j++){
                if(isIllegal(x,j)){
                    v[x][j] = 'Q';
                    matrix.push_back({x,j});
                    dep(cur+1 , n , x + 1 , 0 , v, ans);
                    matrix.pop_back();
                    v[x][j] = '.';
                }
            }
        }

    }
};

找到了！！！双双最优 vector<vector<int>>速度显著高于vector<pair<int,int>>，一修改全部最优！gpt真不行。注意的点是一行找完直接下一行开始，节省时间。这样检查时候，也不用检查行的问题。

class Solution {
public:
    vector<pair<int,int>> matrix;
    vector<vector<string>> solveNQueens(int n) {
        vector<string> v(n);
        for(int i = 0 ; i < n ; i++) v[i].resize(n,'.');
        vector<vector<string>> ans ;
        dep(0,n,0,0,v,ans);
        return ans;
    }
    
    bool isIllegal ( int x, int y){
        for(auto key : matrix){
            if( key.second == y || abs(y - key.second) == abs(x - key.first)){
                return false;
            }
        }
        return true;
    }
    void dep(int cur , int n  , int x, int y,  vector<string> &v , vector<vector<string>> &ans ){
        if(cur == n) ans.push_back(v);
        else{
            for(int j = 0 ; j < n ; j++){
                if(isIllegal(x,j)){
                    v[x][j] = 'Q';
                    matrix.push_back({x,j});
                    dep(cur+1 , n , x + 1 , 0 , v, ans);
                    matrix.pop_back();
                    v[x][j] = '.';
                }
            }
        }

    }
};

二分查找

边界条件太太太容易错了，所以总结了四种情况，够用了

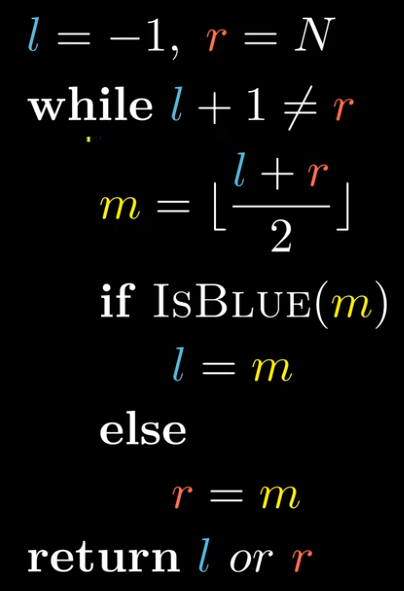
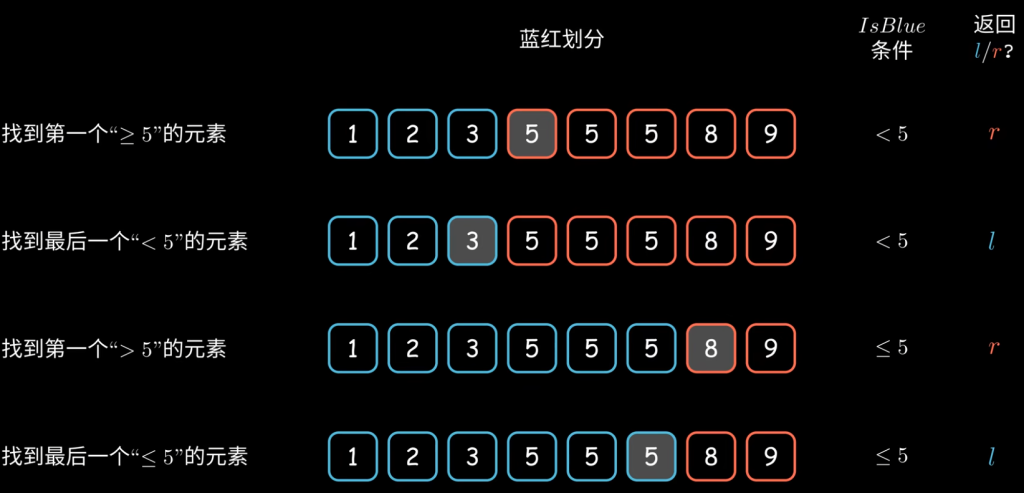
原理来说，中间的m一定在闭区间（0,n-1）合法性没问题。

这个取值，保证左右l,r一定是保持在自己的区间内，不过超越区间。

这样，只要初始的isBlue设置的好，就可以处理所有情况

搜索插入位置

tmd，二分查找就错错错，边界条件不写还真不会

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        int size = nums.size();
        int left = 0, right = nums.size() - 1;
        while(left <= right){
            int mid = left + (right - left) / 2;
            if(nums[mid] < target){
                left = mid + 1;
            }else{
                right = mid - 1;
            }
        }
        return left;
    }
};

使用合理方法，秒了

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        // 超出原本的外面
        int left = -1 , right = nums.size();
        // 想要插入第一个>= target的位置
        while(left + 1 != right){
            int mid = (left + right) / 2;
            if(nums[mid] < target){
                left = mid;
            }else{
                right = mid;
            }
        }
        return right;
    }
};

搜索二维矩阵

nnd，刚学完新方法就给我来特例是吧。这个相当于要求，第一个<=的数字，但是还必须在合理范围内。那就打补丁2333333333。不过不得不说，真的提高了好多好多。

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        int n_x = matrix.size() , n_y = matrix[0].size();
        int up = -1 , down = n_x , left = -1, right = n_y ;

        // 找到第一个<= 元素
        while(up + 1 != down){
            int mid = (up + down ) /2;
            if(matrix[mid][0] <= target){
                up = mid;
            }else {
                down = mid;
            }
        }
        if(up == -1) up = 0;

        while(left + 1 != right){
            int mid = ( left + right) / 2;
            if(matrix[up][mid] <= target){
                left = mid;
            } else {
                right = mid;
            }
        }
        if(left == -1) left = 0;
        return (matrix[up][left] == target);
    }
};

在排序数组中查找元素的第一个和最后一个位置

打补丁，爽。全部拿下

class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) {
        vector<int> ans;
        // 检测<的right 和 >的left。注意取到的值和最后答案不相同要设置为-1
        int n = nums.size();
        int left = -1 , right = n;

        while(left + 1 != right){
            int mid = (left + right ) /2 ;
            if(nums[mid] < target ){
                left = mid;
            }else{
                right = mid;
            }
        }
        if(right != n && nums[right] == target) ans.push_back(right);
        else ans.push_back(-1);

        left = -1 , right = n;
        while(left + 1 != right){
            int mid = (left + right ) /2 ;
            if(nums[mid] <= target ){
                left = mid;
            }else{
                right = mid;
            }
        }
        if(left != -1 && nums[left] == target) ans.push_back(left);
        else ans.push_back(-1);
        return ans;
    }
};

搜索旋转排序数组

最小栈

好没意思的题目

class MinStack 
{
    stack<pair<int,int>> sk;
public:

    MinStack()  {}
    
    void push(int val) 
    {
        sk.push({val,min(val,getMin())});
    }
    
    void pop() 
    {
        return sk.pop();
    }
    
    int top() 
    {
        return sk.top().first;
    }
    
    int getMin() //如果为空的时候是没有最小值的
    {
        return sk.empty() ? INT_MAX : sk.top().second;
    }
};

字符串解码

经典栈

class Solution {
public:
    string decodeString(string s) {
        
        string ans;
        for( auto ch : s){
            if(ch != ']'){
                ans.push_back(ch);
            }else{
                int num = 0;
                string str = "";
                string numStr = "";
                
                // 先读取字母
                while(1){
                    char tmp = ans.back();
                    ans.pop_back();
                    if(tmp == '[') break;
                    str = string(1 , tmp) + str;

                }
                //再读取数字
                while(ans != ""){
                    char tmp = ans.back();
                    if(tmp > '9' || tmp < '0') break;
                    ans.pop_back();
                    numStr = string(1 , tmp) + numStr; 
                }
                num = stoi(numStr);
                for(int i = 0 ; i < num ; i++){
                    ans += str;
                }
            }
        }
        return ans;
    }
};

每日温度

这种没做过，但做一次就明白了。单调栈，把前面比自己小的都杀了，这样巧妙的利用了状态。。当感觉还是很奇技淫巧23333.

class Solution {
public:
    vector<int> dailyTemperatures(vector<int>& temperatures) {
        int n = temperatures.size();
        stack<pair<int,int>> s;
        vector<int> ans(n , 0);//初始就假设你找不到更大的

        for(int i = 0 ; i <  n; i++){
            if(s.empty()) s.push({i , temperatures[i]});
            else{
                // 没空，就一直跑，保持单调减
                while(!s.empty() && temperatures[i] > s.top().second){
                    auto pr = s.top();
                    s.pop();
                    ans[pr.first] = i - pr.first;
                }

                // 现在肯定递减，那么就插入这个
                s.push({i , temperatures[i]});
            }
        }
        return ans;
    }
};

前 K 个高频元素

我成了！会用这些效率大大提高

class Solution {
public:
    vector<int> topKFrequent(vector<int>& nums, int k) {
        // 用pair ，和堆
        auto tmp = [](const pair<int , int> & a ,const pair<int , int> & b){
            return a.first < b.first; 
        };
        priority_queue<pair<int , int> , vector<pair<int,int> >,  decltype(tmp)> p;

        // 记录每一个数字出现数量
        unordered_map<int , int > mp;
        for(auto num : nums){
            mp[num] += 1;
        }

        // 开始插入
        for(auto pr : mp){
            p.push({pr.second , pr.first});
        }

        vector<int> ans;
        for(int i = 0 ; i < k ; i++){
            ans.push_back(p.top().second);
            p.pop();
        }
        return ans;


    }
};

数据流的中位数

维护两个堆，一个大于中位数，一个小于中位数。这样中间的值就是答案。

class MedianFinder {
public:
    // 思路：两个堆，大顶堆和小顶对
    // 大顶堆对前半部分，大顶堆对后半部分
    // 这样每次中位数就是中间俩值
    priority_queue<int> max_queue;
    priority_queue<int , vector<int> , greater<int>> min_queue;
    int l = 0;
    int r = 0;
    MedianFinder() {
        
    }
    
    void addNum(int num) {
        if(l == 0){
            max_queue.push(num);
            l++;
        }
        else {
            if( num > max_queue.top()){
                min_queue.push(num);
                r++;
            } else{
                max_queue.push(num);
                l++;
            }
        }

        if(r > l){
            int temp = min_queue.top();
            min_queue.pop();
            max_queue.push(temp);
            r -- ;
            l ++;
        } else if( l > r + 1){
            int temp = max_queue.top();
            max_queue.pop();
            min_queue.push(temp);
            l --;
            r++;
        }
    }
    
    double findMedian() {
        if((r + l) % 2 == 0) return (double(max_queue.top()) + min_queue.top()) / 2;
        return double(max_queue.top()) ;
    }
};

买卖股票的最佳时机

1还是简单，但是看着原来题解是双指针来着2333。不过现在也解决了

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        // 对于最大值，肯定是当前值减去前面的最小值。
        int maxP = 0;
        int curMin = prices[0];
        int n = prices.size();
        for(int i = 1 ; i < n ; i++){
            maxP = max(maxP , prices[i] - curMin);
            curMin = min(curMin , prices[i]);
        }
        return maxP;
    }
};

跳跃游戏

原理是，如果到当前格子后，走不动了，就false。当然，不用考虑走后一个格子

class Solution {
public:
    bool canJump(vector<int>& nums) {
        int n = nums.size();
        int resSteps = 0;
        for(int i = 0 ; i < n - 1; i++){
            resSteps = max(resSteps , nums[i]);
            if(resSteps == 0) return false;
            resSteps --;
        }
        return true;
    }
};

跳跃游戏 II

还是做出来了，也是最优。但是终于仍然错了好几次23333，不知道影响大不大

class Solution {
public:
    int jump(vector<int>& nums) {
        int n = nums.size();
        int currentMax = 0;
        int nextMax = 0;
        int steps = 0;
        // 从头到尾遍历，记录这一次跳跃范围内的最大值。
        // 注意一下最后的情况。我这里相当于记录的是起跳次数，但最后一次是不需要起跳的。
        for(int i = 0 ; i < n ; i++){
            nextMax = max(nextMax , nums[i]);
            if(currentMax == 0 && i != n-1){
                steps ++;
                currentMax = nextMax;
            }
            currentMax -- ;
            nextMax --;
        }
        return steps;
    }

};

爬楼梯

dp[n] = dp[n-1]+dp[n-2]

class Solution {
public:
    vector<int> v;
    int climbStairs(int n) {
        v.resize(n);
        if(n == 1) return 1;
        else if(n == 2) return 2;
        v[0] = 1;
        v[1] = 2;
        for(int i = 2 ; i < n ; i++){
            v[i] = v[i-1] +  v[i - 2] ;
        }
        return v[n -1];
    }

};

杨辉三角

class Solution {
public:
    vector<vector<int>> generate(int numRows) {

        vector<vector<int>> ans;
        for(int i = 0 ; i < numRows ; i++){
            vector<int> v(i+1);
            for(int j = 0 ; j < i + 1 ; j ++){
                if(j == 0 || j == i) v[j] = 1;
                else{
                    v[j] = ans[i - 1][j - 1] + ans[i - 1][j ];
                }
            }
            ans.push_back(v);
        }
        return ans;
    }
};

打家劫舍

想通一个点，一定可以假设左边那个是用的。因为如果n没有，那么n-1的值其实是一样的，那么也不影响

class Solution {
public:
    int rob(vector<int>& nums) {
        // dp[n] = max(dp[n-2]+nums[n] , dp[n-1])
        int n = nums.size();
        if(n == 1) return nums[0];
        if(n == 2) return max(nums[0] , nums[1]);
        vector<int> maxNums(n);
        maxNums[0] = nums[0] ;
        maxNums[1] = max(nums[0] , nums[1]);
        for(int i = 2 ; i < n ; i++){
            maxNums[i] = max(maxNums[i - 2] + nums[i] , maxNums[i - 1]);
        }
        return maxNums[n - 1];
    }

};

完全平方数

思路就是dp[n] = for each i^2 dp[n – i^2] + 1;

class Solution {
public:
    int numSquares(int n) {
        // 对于所有的小于n的平方数
        // dp[n] = for each i^2 dp[n - i^2] + 1;
        vector<int> v(n + 1);
        vector<int> sqrt2;
        int i = 0;
        while(i * i <= n){
            sqrt2.push_back(i * i);
            i++;
        }
        sqrt2.push_back(i * i);
        v[0] = 0;
        for(int i = 1 ; i < n + 1; i++){
            int minSum = INT_MAX;
            int j = 1 ;

            while(sqrt2[j] <= i){
                if(v[i - sqrt2[j]] < minSum){
                    minSum = v[i - sqrt2[j]];
                }
                j++;
            }
            v[i] = minSum +1;
        }
        return v[n];
    }
};

零钱兑换54

边界条件有点硬凑的感觉，但是做出来了

class Solution {
public:
    int coinChange(vector<int>& coins, int amount) {
        // dp[amount] = for each coin min(dp[amount - coin]);
        vector<int> dp(amount+1,INT_MAX);
        dp[0] = 0;
        for(int i = 1 ; i < amount + 1 ; i++){
            for(auto coin : coins){
                if(i - coin >= 0 ){
                    if(dp[i - coin] != -1){
                        dp[i] = min(dp[i - coin] + 1, dp[i]);
                    }
                }
            }
            if(dp[i] == INT_MAX ) dp[i] = -1;
        }
        return dp[amount];
    }
};

看了看答案，其实也和我一样23333，那不管了

class Solution {
public:
    int coinChange(vector<int>& coins, int amount) {
        int Max = amount + 1;
        vector<int> dp(amount + 1, Max);
        dp[0] = 0;
        for (int i = 1; i <= amount; ++i) {
            for (int j = 0; j < (int)coins.size(); ++j) {
                if (coins[j] <= i) {
                    dp[i] = min(dp[i], dp[i - coins[j]] + 1);
                }
            }
        }
        return dp[amount] > amount ? -1 : dp[amount];
    }
};

单词拆分

经典动态规划

class Solution {
public:
    
    bool wordBreak(string s, vector<string>& wordDict) {
        // 开表
        int n = s.length();
        vector<int> v(n+1 , 0);
        v[0] = 1;
        
        for(int i = 1 ; i < n + 1 ; i++){
            for(auto word : wordDict){
                int word_len = word.length();
                // 
                if(word_len > i) continue;
                int j = 0;
                for( ; j < word_len ; j++){
                    //1 - 1 + 0
                    if(word[j] != s[i - word_len + j ]){
                        break;
                    }
                }
                int isOk = 0;
                if(v[i - word_len] && (j == word_len)) isOk = 1;
                v[i] = max(v[i] , isOk);
            }
        }
        return v[n];
    }
};

最长递增子序列

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        // dp[n] = for each num < nums[n] max (num + 1) 
        int n = nums.size();
        vector<int> v(n);
        v[0] = 0;
        int tMax = 0;
        for(int i = 0 ; i < n ; i++){
            int max_num = 0;
            for(int j = 0 ; j < i ; j++){
                if(nums[j] <nums[i]){
                    max_num = max(max_num , v[j]);
                }
            }
            v[i] = max_num + 1;
            tMax = max(tMax , v[i]);
        }
        return tMax;
    }
};

乘积最大子数组

维护正负两个最大，然后根据当前需要去乘。最后得到最大的乘积

class Solution {
public:
    int maxProduct(vector<int>& nums) {
        int maxNum = INT_MIN;
        int n = nums.size();
        vector<pair<int,int>> v(n);//0是最大正，1是最大负
        // dp[n][0] = max (dp[i-1].first*nums[i] , nums[i]);
        v[0].first = nums[0];
        v[0].second = nums[0];
        maxNum = nums[0];
        for(int i = 1 ; i < nums.size() ; i++){
            if(nums[i] >= 0){
                v[i].first = max(v[i-1].first*nums[i] , nums[i]);
                v[i].second = min(v[i-1].second*nums[i] , nums[i]);
            }else{
                v[i].second = min(v[i-1].first*nums[i] , nums[i]);
                v[i].first = max(v[i-1].second*nums[i] , nums[i]);
            }
            maxNum = max(maxNum , v[i].first);
        }
        return maxNum;
    }
};

分割等和子集

思路如下，转化为数组中是否存在和为sum/2的

class Solution {
public:
    bool canPartition(vector<int>& nums) {
        // 实际问题转化为，数组中，是否存在和为 sum / 2 的
        int n = nums.size() , sum = 0;
        for(auto num :nums) sum += num;

        if(sum % 2 == 1) return false;
        //dp[i][j] 表示用前i个数，是否能够求和到j
        // dp[i][j] = max {dp[i-1][j]//不用这个数就可以 , dp[i-1][j-num] } 
        vector<vector<int>> v(n );//构建数组
        int target = sum / 2 ;
        for(int i = 0 ; i < n  ; i++ ){
            v[i].resize(target+1);
        }

        // 下面讨论，是否能够用前i个数达到和j
        for(int j = 0 ; j < target+1 ; j++){
            for(int i = 0 ; i < n; i++){
                // 如果和为0，可以达到
                if(j == 0) v[i][j] = 1; 
                else if(i == 0) nums[i] == target ? v[i][j] = 1 : v[i][j] = 0;
                else if(j >= nums[i] ) v[i][j] = max(v[i-1][j] , v[i - 1][j - nums[i]]);
                else v[i][j] = v[i - 1][j];
            }
        }
        return v[n - 1][sum / 2];
    }
};

最长有效括号

这道题先可以用栈过一遍。最后剩下的都是不符合规范的，标记为1。最后计算连续0的个数即可。偷懒可以直接开新数组，反正都o(n)，如果想省一点就计算差值，要注意，相当于首尾要有0和n，以保证封闭

不过反复提交了好几次，因为太不细心了。代码一长就会犯很多错误23333.

class Solution {
public:
    int longestValidParentheses(string s) {
        stack<int> sta;
        int n = s.length();
        if(n == 0) return 0;
        // 得到了栈
        for(int i = 0 ; i < n ; i++){
            if(sta.empty()) sta.push(i);
            else{
                if(s[i] == '(') sta.push(i);
                else {
                    if(s[sta.top()] == '(') sta.pop();
                    else sta.push(i);
                }
            }
        }

        // 对于栈每一个元素，标记在数组
        int maxNum = 0 , cur = n;
        if(sta.empty()) return n ;
        int temp ;
        while(!sta.empty()){
            temp = sta.top();
            sta.pop();
            maxNum = max(cur - temp - 1  , maxNum);
            cur = temp;
        }
        maxNum = max(maxNum , temp);
        return maxNum;
    }
};

不同路径

class Solution {
public:
    int uniquePaths(int m, int n) {
        vector<vector<int>> v(m);
        //dp[i][j] = dp[i-1][j]+dp[i][j-1];
        for(int i = 0 ; i < m ;i ++) v[i].resize(n);

        for(int i = 0 ; i < m ; i++){
            for(int j = 0 ; j < n ; j++){
                //在边上，只有一条路可以走
                if(i == 0 || j == 0){
                    v[i][j] = 1;
                }
                else{
                    v[i][j] = v[i-1][j]+v[i][j-1];
                }
            }
        }
        return v[m-1][n-1];

    }
};

最小路径和

很容易dp[m][n] = min( dp[m-1][n] + dp[m][n-1]) + nums[m][n]，这种题真涨成就感。

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        // dp[m][n] = min( dp[m-1][n] + dp[m][n-1]) + nums[m][n]
        
        int m = grid.size();
        int n = grid[0].size();
        vector<vector<int>> dp(m);
        
        for(int i = 0 ; i < m ; i++) dp[i].resize(n);
        for(int i = 0 ; i < m ; i++){
            for(int j = 0 ; j < n ; j++){
                if(i == 0 ||  j == 0){
                    if(i == 0 && j == 0) dp[i][j] = grid[i][j];
                    else if(i == 0) dp[i][j] = dp[i][j-1] + grid[i][j];
                    else if(j == 0) dp[i][j] = dp[i-1][j] + grid[i][j];
                }
                else{
                    dp[i][j] = min(dp[i-1][j] , dp[i][j-1]) + grid[i][j];
                }
            }
        }
        return dp[m-1][n-1];
    }
};

最长公共子序列

class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        // dp[i][j] i表示文本1前i字母，j表示文本2前j字母 dp[i][j] 表示公共的子序列长度
        // dp[i][j] = max(dp[i-1][j-1] + s[i] == s[j] , dp[i][j-1], dp[i-1][j])
        
        int n1 = text1.length() , n2 = text2.length();
        vector<vector<int>> dp(n1);
        for(int i = 0 ; i < n1 ;i++) dp[i].resize(n2);

        for(int i = 0 ; i < n1 ; i++){
            for(int j = 0 ; j < n2 ; j++){
                if( i == 0 || j == 0){
                    if(i == 0 && j == 0) dp[i][j] = int(text1[0] == text2[0]);
                    else if(i == 0) dp[i][j] = max(dp[i][j] = dp[i][j-1] , int(text1[i] == text2[j]));
                    else dp[i][j] = max(dp[i-1][j] , int(text1[i] == text2[j]));
                }
                else{
                    dp[i][j] = max(max(dp[i-1][j-1]+ int(text1[i] == text2[j]) , dp[i][j-1] ), dp[i-1][j]);
                }
            }
        }
        return dp[n1-1][n2-1];
    }
};

最长回文子串

稀里糊涂过的。很多细节边界条件感觉不是特别想的清楚。但是看这里最好是不用动归，但我管你的2333

class Solution {
public:
    string longestPalindrome(string s) {
        //dp[i][j] 表示在[i,j]内是否是回文
        //dp[i][j] = dp[i+1][j-1] && s[i] == s[j]
        //dp[i][i] = true

        int n = s.length();
        vector<vector<int>> dp(n);
        for(int i = 0 ; i < n ;i++) dp[i].resize(n,0);
        pair<int , int> maxPair = {0,0};
        // 斜着遍历，一条一条的
        for(int j = 0 ; j < n ; j++){
            for(int i = 0 ; i < n -j; i++){
                // 如果是第一条，即自己和自己，那肯定回文
                if(j == 0) dp[i][j+i] = 1;
                // 如果是第二条，则是两个，比较两个相同就回文
                else if(j == 1) dp[i][j+i] = int(s[i] == s[j+i]);
                //对于后面的，比较要新加的两个是否相等，且内部要是回文，即dp[i+1][j-1] && s[i] == s[j]
                else{
                    dp[i][j+i] = dp[i+1][j+i-1] && int(s[i] == s[j+i]); 
                }
                //记录最大的长度
                if(dp[i][j+i] && (j > maxPair.second - maxPair.first)){
                    maxPair.first = i;
                    maxPair.second = j+i;
                }
            }
        }
        int x = maxPair.first , y = maxPair.second;
        return s.substr(x,y-x+1);//和下面等价
        // string ans;
        // while(x != y){
        //     ans += s[x++];
        // }
        // ans += s[x];
        // return ans;
        
    }
};

编辑距离

上课讲过的，一下就有感觉可以做了。

不过怎么说呢，还是边界。对于边界两种处理方法，一种是扩大表，比如说要m * n，那么我就造一个 (m + 1) * (n + 1) ，这样边界很快处理，对于核心不用修改。一种是小心考虑边界情况。这个就属于这一种，

class Solution {
public:
    int minDistance(string word1, string word2) {
        // dp[i][j] word1前i个 和 word2前j个，最小的遍历距离
        // dp[i][j] = min{dp[i-1][j] + 1 , dp[i][j-1] + 1 , dp[i-1][j-1] + s[i] == s[j]}
        int n1 = word1.length() , n2 =word2.length();
        vector<vector<int>> dp(n1+1);
        for(int i = 0 ; i < n1+ 1 ; i++) dp[i].resize(n2+1);
        for(int i = 0 ; i < n1 + 1; i++){
            for(int j = 0 ; j < n2 +1; j++){
                if(i == 0 || j == 0){
                    if(i == 0 && j == 0) dp[i][j] = 0;
                        else if(i == 0) dp[i][j] = dp[i][j-1] + 1;
                        else dp[i][j] = dp[i-1][j] + 1;
                }
                else {
                    dp[i][j] = min(min(dp[i-1][j] + 1 , dp[i][j-1] + 1) , dp[i-1][j-1] + int(word1[i-1] != word2[j-1]));
                }
            }
        }
        return dp[n1][n2];
    }
};

颜色分类

又双叒叕一个脑筋急转弯，不过这次一下就看出来了

因为只有三种球，所以只需要统计每种出现的个数。然后再从头到尾遍历一次直接覆盖原数组，完成。

void sortColors(vector<int>& nums) {
        int a_sum = 0 , b_sum = 0 , c_sum = 0;
        int n = nums.size();
        for(int i = 0 ; i < n ; i++){
            if(nums[i] == 0) a_sum++;
            else if(nums[i] == 1) b_sum++;
            else c_sum++;
        }
        for(int i = 0 ; i < n ; i++){
            if(a_sum > 0) {
                nums[i] = 0;
                a_sum --;
            } else if( b_sum > 0){
                nums[i] = 1;
                b_sum --;
            } else {
                nums[i] = 2;
                c_sum --;
            }
        }
    }

下一个排列

2333，说人话就是
找出这个数组排序出的所有数中，刚好比当前数大的那个数
比如当前 nums = [1,2,3]。这个数是123，找出1，2，3这3个数字排序可能的所有数，排序后，比123大的那个数 也就是132

我大概做到了可以保证比开始大，但是没有恰好下一个。这种题就是纯数学题，想明白就容易了。

步骤分为三步：

void nextPermutation(vector<int>& nums) {
        //首先找到第一个逆序排列的
        // 遍历过的部分（倒着看）一定是按照从小到大排列
        int i = nums.size() - 2 ;  
        while(i >= 0){
            if(nums[i+1] > nums[i]) 
                break;
            i--;
        }

        //再从后面中，找到恰好比当前大的值
        // 如果不是-1，则说明不需要找值
        if(i != -1){
            int j = nums.size() - 1;
            while(j > i){
                if(nums[j] > nums[i]){
                    swap(nums[j] , nums[i]);
                    break;
                }
                j--;
            }
        }
        //最后，后半部分reverse
        reverse(nums.begin() + i + 1 , nums.end());
    }