考试语言:中文
考试题型:简答分析设计题(65分)和计算题(35分)
注意事项:65分的简答分析设计题考察课程第1讲—第5讲和第7讲相关内容概念和方法的理解和掌握;35分的计算题考察对于第6章和丁玥老师部分算法内容的掌握。
Inotherword:基本全考
考试建议:带上机器学习资料,打印PPT(仅作查漏补缺)
课程概要
- 聚类:是一个把数据对象(或观测)划分成子集的过程,每个子集是一 个簇 分类:是一种重要的数据分析形式,它提取刻画重要数据类的模型
- 关联分析:若两个或多个变量的取值之间存在某种规律性,就称为关联
- 数据总结:继承于数据分析中的统计分析,其目的是对数据进行浓缩, 给出它的紧凑描述
- 偏差检测:基本方法是寻找观测结果与参照值之间有意义的差别,对分 析对象中少数的、极端的特例进行描述,解释内在原因
- 预测:通过对样本数据(历史数据)的输入值和输出值的关联性学习, 得到预测模型,再利用该模型对未来的输入值进行输出值预测
认识数据
数据类型
- 记录类型:关系记录、数据矩阵(如数值矩阵交叉表)、文档数据(文本可表示为词频向量)和交易数据
- 图和网络类型:万维网、社会或信息网络以及分子结构
- 有序类型:视频数据(图像序列)、时间序列数据、交易序列等 sequential 数据和基因序列数据
- 空间、图像和多媒体类型:地图等空间数据、图像数据和视频数据
数据对象与属性类型
- 数据对象:数据集由数据对象组成,代表实体,如销售数据库中的顾客等,也被称为样本等,通常用属性描述,对应数据库的行,属性对应列。
- 属性类型:
- 标称属性:定性,代表类别等,如头发颜色、婚姻状况,可用数表示但数学运算无意义。
- 二元属性:定性,只有两个状态,对称的如性别,非对称的如医疗化验结果,通常对重要结果用 1 编码。
- 序数属性:定性,值有意义的序,如可乐杯大小、成绩,可用于等级评定调查,可通过数值属性离散化得到,能用众数和中位数表示中心趋势。
- 数值属性:定量,用整数或数值表示,分为区间标度(如温度、日期,有相等单位尺度,无真正零,不能计算比率)和比率标度(如开氏温度、货币量,有固有零点,可计算比率)。
- 离散与连续属性:离散属性具有有限或无限可数个值,如可乐杯大小等,二元属性是其特殊情况;连续属性通常用实数表示,如温度等。
数据的基本统计描述
中心趋势度量
可通过均值(Mean,算数均值、加权平均、截尾均值[去掉几个少数极端数值])、中位数(Median,有序数据中间值,N 为偶数时按公式计算)、众数(Mode,出现最频繁的值,可能多个)、中列数(最大最小值平均值)来度量中心趋势。
中位数近似值计算(根据区间)

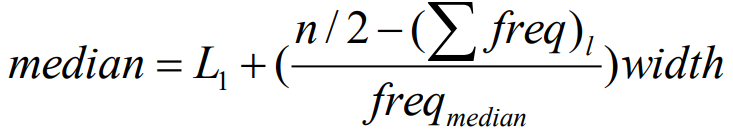
总频数为n,L1是中位数区间下线,(∑freq)l是中位数区间之前累积的频率freqmedian是中位数区间频率,width是中位数区间的宽度
总频率计算得200+450+300+1500+700+44=3194
n/2为1597,对应在21-50区间,之前的累计评频率950
freqmedian=1500,width=50-21=29
最后可以得到,median=21 + (1597-950)*29/1500 = 33.51
众数近似值
对称数据:均值、中位数、众数一致
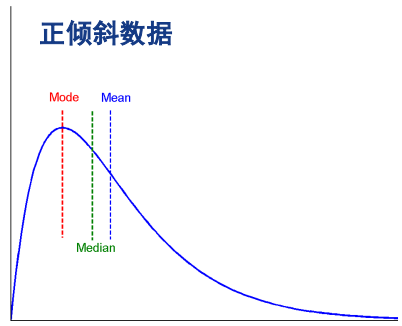
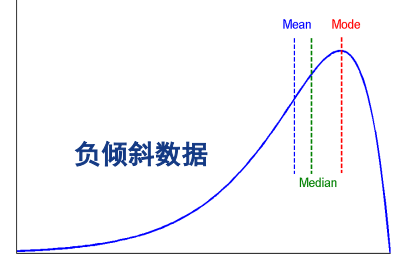
对于适度倾斜(非对称)的单峰数值数据,众数近似值计算:
mean – mode = 3 x (mean – median)
数据散布
- 极差:最大值减最小值
- 分位数:把数据分成n个相同的集合,如 2 – 分位数即中位数,4 – 分位数有 3 个点分数据为四部分等
- 四分位数极差:IQR=Q3-Q1,即75%分位数-25%分位数
- 孤立点(异常值):高于 Q3 或低于 Q1 1.5×IQR 的点
- 五数概括:min(Q1-1.5IQR),Q1,median,Q3 ,max(Q3+1.5IQR)
- 盒图:数据分布的一种直观表示,可以展示中心倾向,偏度,分布,离群值。内容如下:
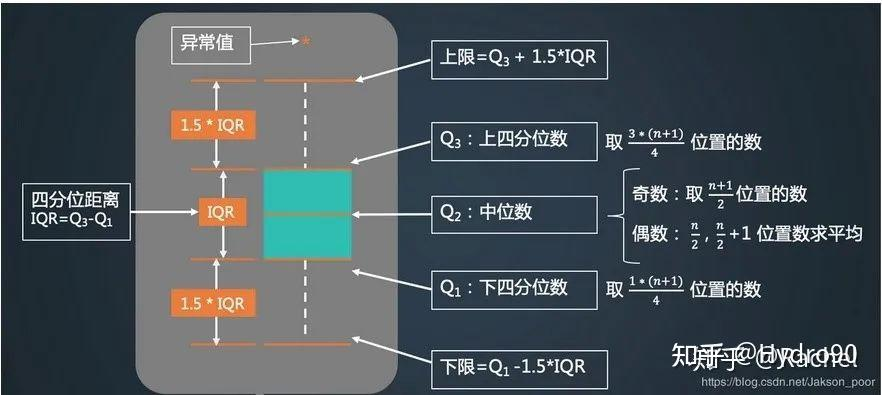
- 方差:公式如下,标准差为方差平方根
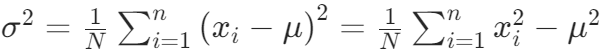
图形展示
对于以下数据:
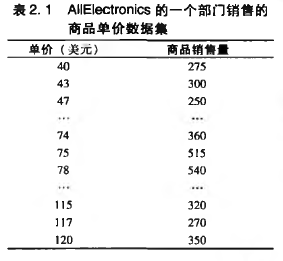
- 一元分布
- 分位数图:一个xi和一个百分比数fi配对。用来观察变量x的分布
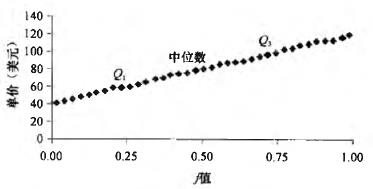
- 分位数–分位数图:观察两组x的分布,判断一个分布到另一个分布是否有漂移
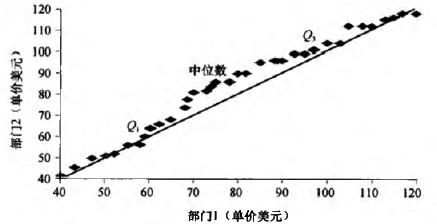
- 直方图:对于标称属性X的每一个值画一个柱子表示频率
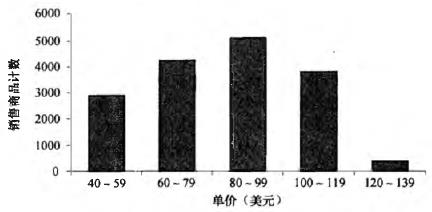
- 分位数图:一个xi和一个百分比数fi配对。用来观察变量x的分布
- 二元分布:
- 散点图:观察两个数值变量(点簇和离群点)及其相关联系的可能性
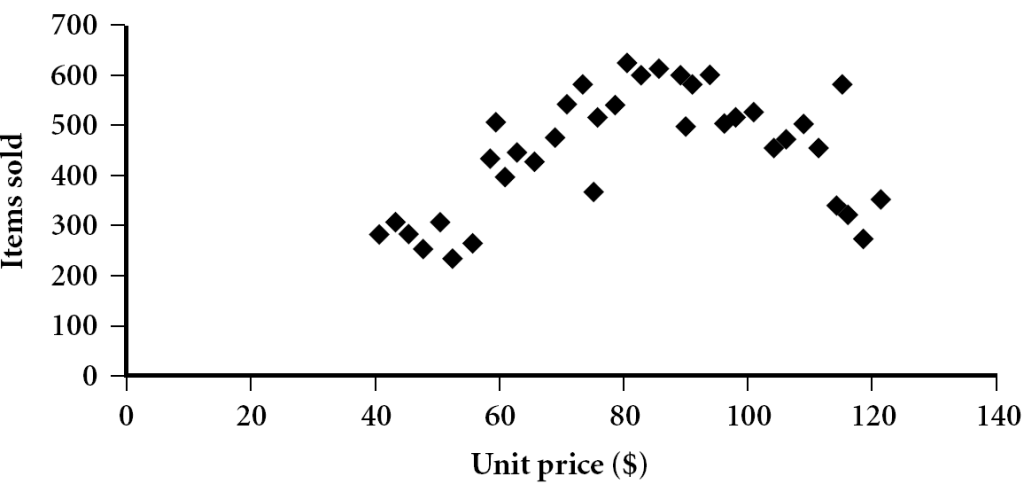
- 散点图:观察两个数值变量(点簇和离群点)及其相关联系的可能性
数据可视化
- 基于像素的可视化技术
- 将 m 维数据集映射到 m 个窗口的像素(每个维度一个),像素深浅表示对应的值的大小

- 缺点:
- 线性安排填充窗口效果不好,对于同一行的像素,应该是彼此贴近的
- 解决:使用空间填充曲线(如Hilbert curve,Graycode,Z-curve等)
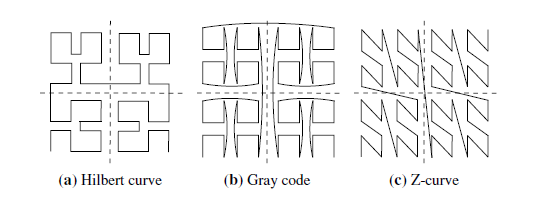
- 解决:使用空间填充曲线(如Hilbert curve,Graycode,Z-curve等)
- 空间浪费多,比较不明显
- 解决:采用圆弓分割技术,显示多维度之间的关系
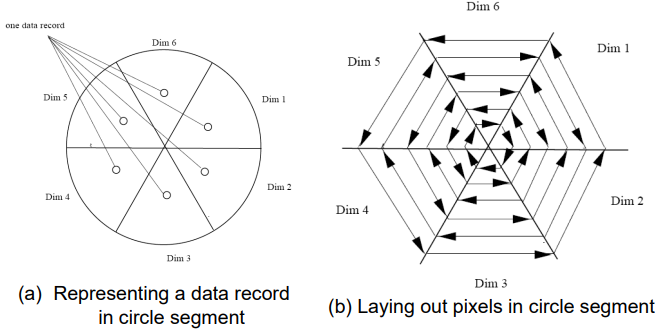
- 解决:采用圆弓分割技术,显示多维度之间的关系
- 线性安排填充窗口效果不好,对于同一行的像素,应该是彼此贴近的
- 缺点:
- 将 m 维数据集映射到 m 个窗口的像素(每个维度一个),像素深浅表示对应的值的大小
- 几何投影可视化技术:解决高维空间二维显示,散点图用笛卡尔坐标显示二维数据,散点图矩阵是 n×n 网格展示 n 维数据,平行坐标用 n 个平行轴,数据记录用折线表示。
- 基于图符的可视化技术:用图符可视化数据值,切尔诺夫脸用面部特征表示多维数据,人物线条画用四肢和躯干表示多维数据。
- 层次可视化技术:将维划分子集按层次可视化,如 “世界中的世界” 和树图(如 Google 新闻报导可视化)。
- 可视化复杂对象和关系:标签云用字体大小或颜色表示标签重要性,疾病影响图用结点大小和边宽度表示疾病流行程度和相关性。
度量数据相似性和相异性
为什么要度量这个相似性和相异性?
商家可以通过聚类发现顾客群体,更具针对;离群点分析可以检测显著不同的对象,例如银行发现诈骗;医疗领域可以通过最近邻分类给患者分配诊断标签or疾病类型。
相似性:描述两个数据相似程度的数值,范围[0,1],越大越相似;
相异性:描述两个对象不同程度的数值,如距离,一般越不相似越大,最小通常为0
那怎么描述这个数值呢?用矩阵
数据矩阵与相异性矩阵
数据矩阵: n×p 矩阵存放 n 个对象 p 个属性
相异性矩阵:n*n的上/下三角矩阵表示两个对象之间的相异性值,反过来相似性 sim (i)=1-d (i)。可以看到对角线都为0,这是因为一个对象和自己的差别(相异性)为0
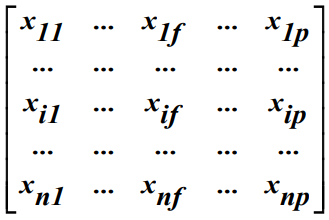
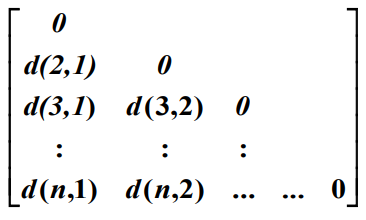
计算相异性
标称属性:使用不匹配率 d(i,j) = (p-m)/p,m是匹配属性数(i和j取值相同状态的属性),p是属性总数。如 1是A ,2是B,3是A;则sim(1,2)=(1-0)/1=1;sim(1,3)=(1-1)/1=0;
二元属性:只有两种状态0和1,0表示不出现,1表示出现。那么如何计算呢?
对于对象I和J,定义:
q 是对象 I 和 J 都取1的属性数
r 是对象 I 取1,对象J取0的属性数
s 是对象 I 取0,对象J取1的属性数
t 是对象 I 和 J 都取0的属性数

那么得到二元属性对称时相异性 d(i,j) = (r+s)/(q+r+s+t)
但有时,认为负匹配不重要,忽略掉t,此时得到的是非对称相异性,此时得到:
d(i,j) = (r+s)/(q+r+s)
此时的相似度被称为Jaccard系数,即:
simJaccard=q/(q+r+s)
数值属性:刻画对象之间相异性的距离度量
欧氏距离(闵可夫斯基距离h=2),曼哈顿距离(闵可夫斯基距离h=1),闵可夫斯基距离,切比雪夫距离(h->∞,得到上确距离,各坐标数值差中的最大值为将产生两个对象的最大值差)
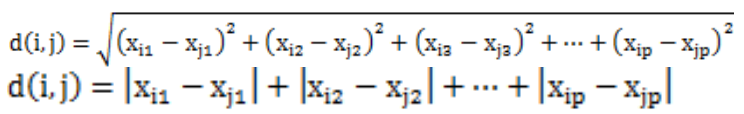
序数属性:将值映射到排位,再均匀映射到 [0,1],用距离度量计算。注意需要覆盖所有的可能取值。
如评分有优良中差四种,哪怕只出现优良中组合,那么也应该是(1,0.66,0.33);d(i,j)二者直接相减就可以
混合属性:针对数据结构,把上面四个全部都结合起来。
对象I和j之间的相异性d(I,j)定义为:
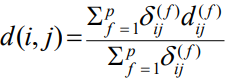
- 针对每一个属性f,对于其对I和J之间的贡献度dij(f):
- 对于二元属性/标称属性,相等为0,相异为1
- 对于序数属性,映射到[0,1]然后当作数值属性
- 对于数值属性,映射到[0,1]然后计算
- 对于指示符δij(f):
- 如果两个值有任一个缺失,或者在该属性是非对称二元属性的前提下二者值均为0时,δij(f)=0;其余情况为1
例题:text-1为标称属性,test-2为包括优良中的序数属性,test-3为数值属性
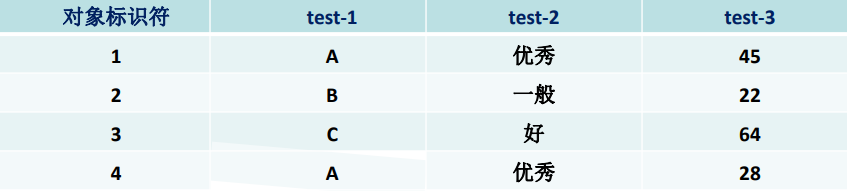
对于test1,单个属性情况只有相同为1,其余为0

对于test2,映射后优良中分别为(1,0.5,0),因此

对于test3,以最大值64到22的差来格式化,因此1为(45-22)/(64-22)=0.55,2为0,3为1,4为(28-22)/(64-22)=0.14,因此d(1,2)=0.55,d(1,3)=0.45,d(1,4)=0.40…….

最后,由于没有出现值的缺失,也没有出现非对称二元属性,直接前三个矩阵对应位置相加求平均即可
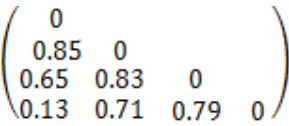
稀疏数据度量:如文档词向量频率,采用余弦相似度 sim(x,y)= cos(x,y) = xy / (||x|| ||y||),二元属性时候称为Tanimoto 系数,此时余弦函数可以写成sim(x,y) = xy/(xx+yy-xy)
数据预处理
为什么要对大数据预处理呢?
原始数据常存在不完整、重复、错误等问题,直接使用会严重影响决策的准确性和效率,预处理通过清洗、集成等任务提升数据质量,是分析的关键前提。
对于数据质量,有几个衡量因素:
- 准确性 | 数据正确性 | 设备故障、输入错误、传输错误等
- 完整性 | 无缺失属性 | 属性未记录、输入时忽略等
- 一致性 | 数据统一 | 部分数据修改、历史数据忽略等
- 时效性 | 数据及时更新 | 月末数据未及时提交等
- 可信性 | 数据可信度 | 因为历史错误导致用户不再信任
- 可解释性 | 数据易理解性 | 编码复杂难解释
基于数据源的脏数据分类:
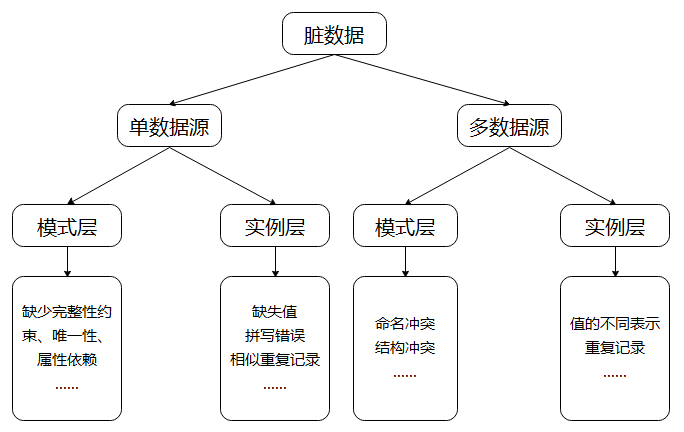
那么如何与处理呢?就是下面四步了数据清洗,数据集成,数据规约,数据变换与离散化
数据清洗
why需要?现实数据因设备故障、输入错误等原因常为 “脏数据”,直接使用影响分析准确性,数据清洗是数据预处理关键环节。
脏数据类型: 缺失值(属性值或属性缺失),噪声数据(错误或偏离值),不一致数据(编码 / 名称差异),人为因素(故意填写错误)
缺失值处理方法
| 方法 | 说明 | 适用场景 |
|---|---|---|
| 忽略元组 | 删除含缺失值元组 | 类标号缺失且缺失比例大;当每个属性缺失值百分比很大时候性能很差 |
| 人工填写 | 手动补全 | 数据量小且重要;但费事 |
| 全局常量填充 | 用固定值(如 unknown)填充 | 快速处理 |
| 中心度量填充 | 用均值 / 中位数填充 | 数值型数据 |
| 同类统计量填充 | 用同类样本均值 / 中位数填充 | 分类数据(如按风险等级分顾客),相对科学 |
| 推理填充 | 回归、决策树等推断最可能值 | 需建模推断 |
噪声处理方法
- 分箱平滑
- 步骤:排序→分箱→按箱均值 / 中位数 / 边界值平滑。
- 如:序列{4,8,15,21,21,24,25,28,34},先划分为{4,8,15}{21,21,24}{,25,28,34}
- 均值光滑:{9,9,9}{22,22,22}{29,29,29}
- 边界光滑:{4,4,15}{21,21,24}{25,25,34}(每个数选择离自己最近的边界值)
- 回归:用函数拟合数据(如线性回归),使一个属性可以预测另一个
- 聚类:删除离群点
- 计算机和人工检查结合:检查可疑的值,结合人工手段
基于ETL的数据清洗:抽取→转换→加载,将异构源数据清洗后加载至数据仓库。使用如kettle和sql语句
pandas数据分析库:数据对齐和灵活操作比传统 SQL 更便捷。
数据集成
定义:将多源异构数据合并为一致视图的过程,需解决分布性和异构性问题。
主要任务:
实体识别:识别多源数据中的同一实体,包括模式集成(如属性等价映射 A.cust-id≡B.cust-#)和属性匹配(处理结构差异与表达差异,如对于0值空白值处理)。
冗余分析:通过相关分析检测冗余属性,度量一个属性能多大程度蕴含另一个。如年收入可由月收入衍生。对于标称属性,使用Χ2 (卡方)检验;对于数值属性,使用相关系数和协方差检测变换
数据相关性分析方法
Χ2 (卡方)检验
问题:性别(男/女)与是否喜欢某款游戏(是/否)是否存在显著关系?
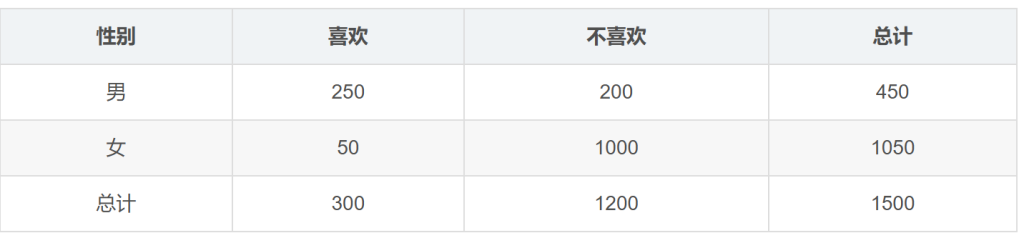


相关系数/皮尔森积矩系数
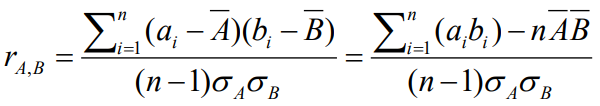
其中,n是元组的个数,▔A▔B分别是是A和B的均值,σA 和 σB 分别是A和B的标准差,Σ(aibi )是AB叉积和。
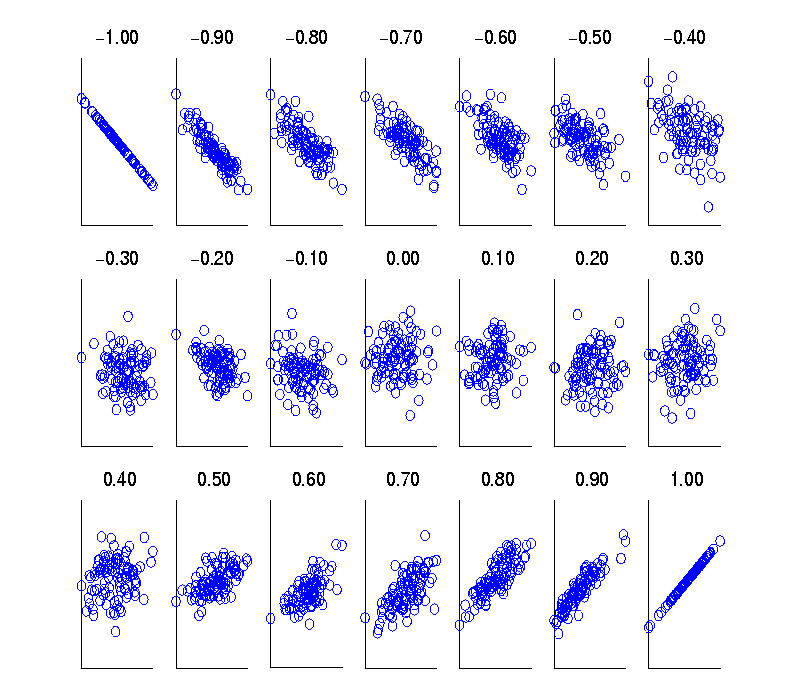
If rA,B > 0, A and B正相关(A随着B值的增加而增加),该值越大,相关性越强
If rA,B = 0,A and B独立
If rAB < 0, A and B负相关
数据集成方式分类
| 分类类型 | 定义 | 特点 | 典型引擎 / 应用 |
|---|---|---|---|
| 批量集成 | 定时 / 触发式全量处理数据 | 非高峰执行,处理大数据量 | Hadoop MR、Spark、Kettle |
| 增量集成 | 仅传输新增 / 变更数据 | 减少资源消耗,依赖时间戳 / 日志 | 电商订单同步 |
| 准实时集成 | 数据变化后短时间内同步 | 分钟到小时级延迟,轮询 / 订阅实现 | Storm、Spark Streaming |
| 实时集成 | 数据变更时立即同步 | 事件驱动,低延迟决策 | Flink、Kafka Streams |
| 事件集成 | 基于事件驱动架构触发数据处理 | 实时响应事件(如异常告警) | Kafka、RabbitMQ |
| 同步集成 | 系统间即时双向数据传输 | 强事务一致性,实时交互 | API 接口查询用户信息 |
| 异步集成 | 数据传输不立即响应 | 缓解系统负载,非实时场景 | 批量邮件发送 |
| 流处理 | 实时处理连续数据流 | 高吞吐量,适用于日志 / 传感器数据 | Kafka Streams、Flink |
| 复制 | 数据副本同步至其他位置 | 用于备份 / 负载均衡,分同步 / 异步复制 | 数据库主从复制 |
| 归档 | 长期保存不常访问的数据 | 压缩存储,节省主存储资源 | 医疗数据存档 |
主流集成架构对比
| 架构类型 | 核心特点 | 适用场景 | 典型工具 / 技术 |
|---|---|---|---|
| 点对点架构 | 系统直接连接,单独建立集成通道 | 少量系统集成 | 自定义 API、RabbitMQ |
| 集中式架构 | 通过 ESB 等中心节点路由数据 | 企业内部多系统实时通信 | MuleSoft、中间件 |
| 数据仓库架构 | ETL/ELT 处理后存储至中央仓库 | 企业级 BI 报表、历史数据分析 | Informatica PowerCenter、DataStage |
| 数据湖架构 | 存储多格式原始数据,按需处理 | 大数据分析与机器学习 | HDFS、Amazon S3、Delta Lake |
| 服务导向架构(SOA) | 标准化接口共享服务,松耦合设计 | 异构系统集成(如银行与第三方支付) | Web Services、ESB |
| 微服务架构 | 应用拆分为独立小服务,轻量级通信 | 互联网快速迭代系统 | Spring Cloud、Kubernetes |
| 虚拟化架构 | 通过抽象层提供统一数据访问接口 | 跨地域实时数据查询 | Denodo 等数据虚拟化工具 |
| 云化集成架构 | 基于云服务实现集成,弹性扩展 | 多云 / 混合云环境 | AWS Glue、Azure Data Factory |
2024 年数据集成技术的重要发展方向有哪些?
①实时流处理与批处理融合,如基于 Flink 的 CDC 数据捕获;②云原生集成工具普及,支持跨多云环境;③AI 与大模型整合,实现自动化数据质量修复和动态 ETL(如大模型处理音视频数据)。
数据规约
定义:获取数据集减少后的表示。虽规模更小但能保持原始数据的分析结果,解决数据库存储量大(数兆兆字节)和复杂数据分析耗时长的问题。
why需要?防止维数灾难、消除无关特征、降低噪音、减少数据挖掘的时间和空间成本。
主要策略
| 策略类型 | 核心技术 | 具体方法 |
|---|---|---|
| 维规约 | 降维技术 | 小波变换、主成分分析 (PCA)、属性子集选择、特征生成 |
| 数量规约 | 参数化方法 | 回归分析(线性 / 多元回归)、对数 – 线性模型 |
| 非参数化方法 | 直方图分析(等宽 / 等频分区)、聚类分析、抽样(简单随机 / 分层抽样)、数据立方体聚集 | |
| 数据压缩 | 信息压缩 | 字符串压缩(无损)、音视频压缩(有损) |
小波变换
emmm只看得懂哈尔小波
- 原理:使用层次金字塔算法,每次迭代将数据减半,通过光滑和差分函数提取低频和高频特征,最终选择小波系数实现降维。
- 步骤:输入数据长度需为 2 的整数幂,递归应用光滑和差分函数,直至数据集长度为 2。
e.g.假设一维图像的像素值为:[9, 7, 3, 5]
- 第一层分解:求均值与差值
- 分组求均值
- 将数据分为两组
[9, 7]和[3, 5],计算每组平均值 - 得到[8, 4]
- 将数据分为两组
- 求细节系数(差值)
- 第一组细节:
9 - 8 = 1(或(9-7)/2 = 1) - 第二组细节:
3 - 4 = -1(或(3-5)/2 = -1) - 细节系数:[1, -1]
- 第一组细节:
- 第一层变换结果:
[8, 4, 1, -1](前两位为均值,后两位为细节)
- 分组求均值
- 第二层分解:递归处理均值
- 对第一层的均值
[8, 4]重复上述过程:- 均值计算:
(8+4)/2 = 6 - 细节系数:8 – 6 = 2
- 均值计算:
- 第二层变换结果:
[6, 2, 1, -1](其中6为全局均值,2为次低频细节,1和-1为高频细节)
- 对第一层的均值
主成分分析 (PCA)
步骤:标准化数据→计算正交主成分→按方差降序排列→保留前 k 个主成分。
以以下数据为例
A = [2.5, 2.4]
B = [0.4, 0.7]
C = [2.2, 2.9]
1.计算样本均值X及协方差矩阵S

定义协方差及协方差矩阵(以2维为例,若三维则为xyz),(n为样本数量)


在例子中:


2.解出协方差矩阵S的特征值λ,即|S-λI|=0的解

解二元一次方程得

进而得到与λ对应的特征向量(即Sv=λv)
特征向量满足如下式子:

需要设v=[x,y]然后解出x,y的比例,再归一化到单位长度
对于λ1:

解得

以上两个约等于是因为计算误差导致的,实际上会是一个值。
再进行归一化,v1=[0.713,-0.696]
对于λ2同理,v2=[0.696,0.713](因为是2维所以可以直接看出来,三维不行)
两个主成分的表示:

主成分的贡献度p:(经证明主成分的方差就是特征值大小)

对示例情况:
F1贡献度=0.06/(0.06+2.53)=0.02
F2贡献度=2.53/(0.06+2.53)=0.98
可以根据贡献度从大到小,对所有主成分进行排序,然后根据累计贡献度要求选出前几个主成分
数量规约方法详解
- 回归分析
- 线性回归:Y = wX + b,通过最小二乘法估计系数。
多元回归:Y = b0 + b1X1+ b2X2,处理多自变量场景。
- 线性回归:Y = wX + b,通过最小二乘法估计系数。
- 对数 – 线性模型:近似离散多维概率分布,用于维规约和数据光滑。
- 直方图分析:将数据划分为等宽或等频区间,如销售额数据按季度等频分区。
- 聚类分析:按相似度分簇,存储簇的质心和直径,如客户分群。
- 抽样方法
- 简单随机抽样,等概率选择样本,如无放回 / 有放回抽样
- 分层抽样,按数据分布分层抽取,如处理偏斜数据
- 数据立方体聚集:多维度汇总数据,如按年汇总销售额(1997 年$1,568,000、1998年$2,356,000、1999 年 $3,594,000)。
数据压缩
字符串压缩:采用无损算法,如文本压缩。
音视频压缩:有损压缩,支持渐进细化,如视频流传输。
维规约和数量规约也可以视为某种形式的数据压缩
数据变换与数据离散化
通过变换将整个数据集的给定属性的值映射到新的值,每个老的值都能通过新的值识别
- 光滑Smoothing: 去除数据中的噪声(数据清理的方法)分箱、回归、聚类
- 属性构造Attribute/feature construction(数据规约方法)由给定的属性构造新的属性并添加到属性集中
- 聚集Aggregation: 对数据进行汇总,构造数据立方体(数据规约方法)
- 规范化Normalization: 把属性数据按比例缩放,使之落入特定大小区间
- 最小-最大规范化[min-max normalization]
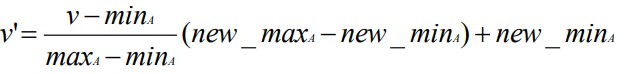
- Z分数规范化z-score normalization
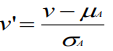
- 小数定标规范化normalization by decimal scaling
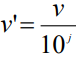
- 通过移动数据 的小数点位置来进行标准化。小数点移动的位数取决于数据绝对值的最大值
- 最小-最大规范化[min-max normalization]
- 离散化Discretization: 将连续的属性分割为有间隔的
- 方法:分箱(见前文,下同),直方图,聚类分析,决策树分析,相关分析(卡方)
决策树
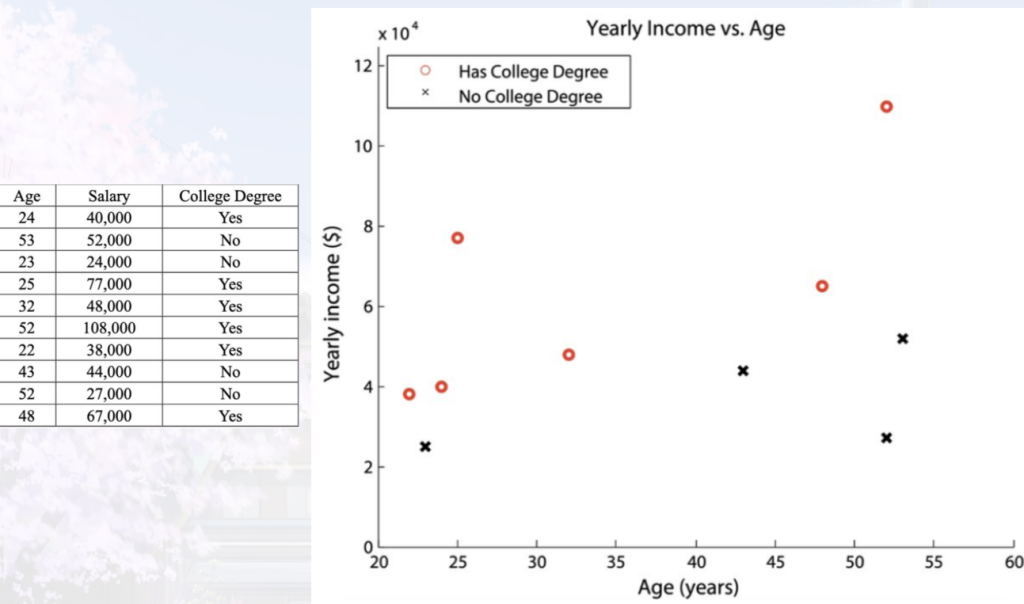
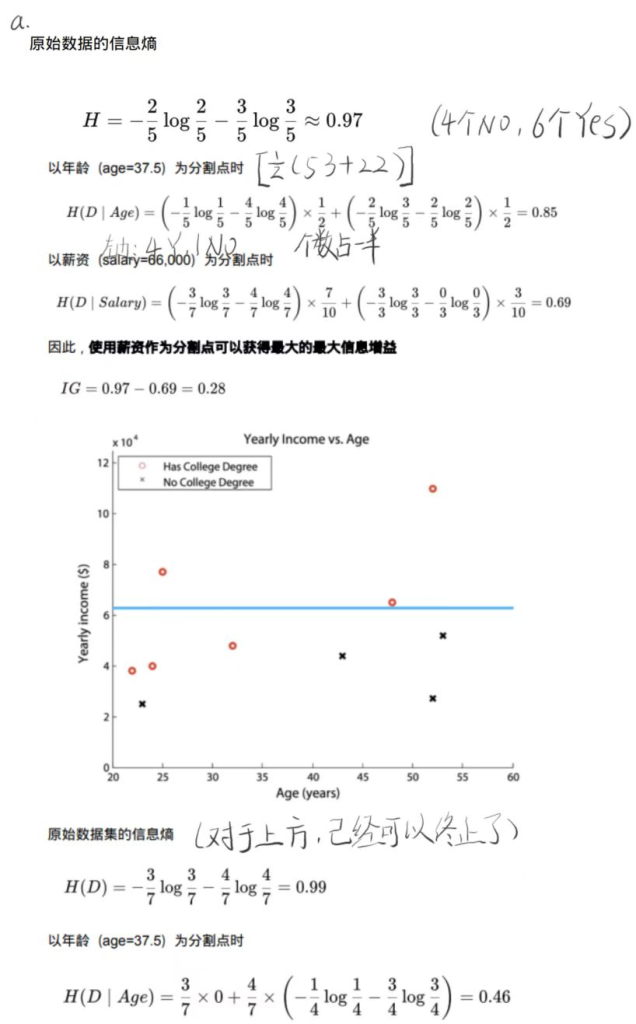
概念分层:递归通过收集和更高层次的概念(如青年,成年,或高级)取 代低层次的概念(如年龄数值)减少数据
数据仓库与联机分析处理
前言
基本概念
定义:数据仓库是面向主题、集成、随时间变化且非易失的数据集合,用于支持管理决策过程。
与OLTP区别:
| 对比项 | OLTP | OLAP |
| 用户 | 办事员、IT 专业人员 | 知识工人 |
| 功能 | 日常操作 | 决策支持 |
| 数据 | 当前、详细 | 历史、汇总 |
| 操作 | 读 / 写 | 大量扫描 |
| 工作单位 | 短事务 | 复杂查询 |
| 数据规模 | 100MB-GB | 100GB-TB |
架构:三层架构,包括底层数据仓库服务器、中间 OLAP 服务器、前端客户工具层。
模型:
企业仓库:搜集跨越整个组织的主题信息。
数据集市:企业数据的子集,针对特定用户。
虚拟仓库:操作数据库上的一系列视图。
多维数据模型:
星型模式:事实表在中心,连接维表。
雪花模式:维表规范化,进一步分解。
事实星座模式:多个事实表共享维表。
数据指标体系设计与应用实践
数据指标
定义:从业务中抽象出可描述业务现状的度量值,如电商的 GMV、用户付费率等。
分类标准
- 业务逻辑
- 北极星指标,指引业务发展的重要指标,如电商 GMV
- 结果指标,北极星指标拆分的子目标,如成交用户数
- 过程指标,达成结果的过程指标,如点击 UV
- 运营指标,业务运营模式相关,如商品库存
- 监控指标,业务外部不可控因素,如竞品数据
- 构成
- 原子指标,不可再拆分,由统计维度、度量、汇总方式组成,如日活跃用户数量
- 派生指标,由原子指标等构成,分事务型、存量、复合型,如付费转化率
评价标准
- 简单易懂:含义无歧义,如 GMV 易理解,弹出率定义复杂少用。
- 具可比性:可在不同时间段等比较,如渗透率排名、同比变化。
- 是比率:如付费转化率比付费人数更直观。
- 改变行为:先见性指标如复购率可预警,后见性指标如退货率提示问题。
注意问题
- 定性与定量指标结合:定量如销售额,定性如用户评价可转化为定量。
- 警惕虚荣指标,选择可执行指标:如总注册用户数,可由活跃用户占比等替代。
- 先见性与后见性指标都重要:先见性如活跃率,后见性如流失率。
- 区分相关性与因果性指标:相关不一定因果,需多问 “为什么”。
数据指标体系
- 定义:多个关联指标按逻辑和层级组织,用于监控业务。
- 要素
- 北极星指标:评价业务最重要的指标,如交易类产品的 GMV。
- 核心指标:北极星指标拆解的过程指标,如成交用户数。
- 分析维度:减少平均数陷阱,如时间、地区、用户类型。
- 作用
- 形成标准化衡量指标,监控业务发展。
- 通过指标分级治理,快速定位问题。
- 减少重复工作,提高分析效率。
- 构建流程
- 指标规划:明确业务目标、构建数据字典。
- 数据采集和加工:明确字段类型、上报时间和方式。
- 报表呈现:选取合适指标、维度,用 BI 工具呈现。
- 应用:监控业务、上卷下钻排查异动。
构建方法论
- 步骤
- 目标化:明确业务目标,梳理北极星指标。
- 模块化及流程化:梳理业务流程,明确核心指标,用 AARRR、UJM 模型。
- 层级化:数据指标分级下钻,用 MECE 模型。
- 维度化:选择维度实现上卷下钻。
- 模型:指导构建完整而清晰的数据指标体系的方法论
- OSM 模型:Object(业务目标)、Strategy(行动策略)、Measure(评估指标)。
- AARRR 模型:用户获取、激活、留存、付费、推广。
- UJM 模型:用户旅程地图,梳理业务流程。
- MECE 模型:指标相互独立、完全穷尽。
构建案例
- 场景:职场在线教育 App 用户注册转化。
- 步骤
- 明确北极星指标:处于发展期过渡阶段,北极星指标为课程收入(GMV),辅助指标为优质活跃用户数量。
- 梳理过程指标:按 AARRR 模型,过程指标为新用户数量、活跃用户数量、留存用户数量、付费用户数量、分享用户数量。
- 指标下钻分级:如 GMV 下钻为成交用户数和平均客单价,再下钻为点击 UV 和访购率等。
- 添加分析维度:用户类型、来源渠道、设备信息、时间周期等。
数据埋点
- 定义:采集用户行为数据的方式,是获取数据指标体系数据的关键。
- 分类
- 普通埋点:简单采集基本信息,如 PV、UV。
- 事件埋点:精准采集用户操作及元素属性,如动作发生时间、内容。
- 设计步骤
- 确认事件与变量:如用户注册事件,变量为注册数量。
- 确认触发时机:如用户完成注册资料填写时触发用户获取事件。
- 确认上报机制:选择实时或异步,客户端或服务器上报。
- 统一字段名:如消费金额统一用 Amount 字段。
- 统一表结构:分用户基础信息层、行为信息层等。
- 明确优先级:根据指标体系优先级确定埋点优先级。
数据仓库
定义:数据仓库是面向主题、集成、随时间变化且非易失的数据集合,用于支持管理决策过程。
特点:
面向主题:围绕顾客、产品等主题组织数据。
集成:整合多个异种数据源,需数据清理和集成。
时变:存储历史数据(如过去 5-10 年),关键结构含时间元素。
非易失:物理上与操作数据库分离,仅需初始装载和访问。
操作型数据库主要支持OLTP联机事务处理,数据仓库主要支持OLAP联机分析处理
架构与模型:
三层架构:底层数据仓库服务器、中间 OLAP 服务器、前端客户工具。
模型:企业仓库(跨组织主题)、数据集市(部门子集)、虚拟仓库(操作数据库视图)。
数据仓库建模
- 数据立方体:
- 由维表和事实表组成,维如时间、产品,事实表含度量(如销售额)。
- 如将多张二维表的数据合并成一个大立方体,可以是很多维
- 方体格:n 维数据立方体有\(\prod_{i=1}^{n}(L_{i}+1)\)个方体,如 10 维 5 层方体数约为510≈9.8×106。
- 由维表和事实表组成,维如时间、产品,事实表含度量(如销售额)。
- 概念模型:
- 星型模式:事实表居中,连接维表,无冗余。
- 雪花模式:维表规范化,进一步分解,如城市维拆分为城市、省份表。
- 事实星座模式:多个事实表共享维表,如销售和发货事实表共享时间维。
- 维与度量:
- 概念分层:如 location 的 city<province<country。
- 度量分类:分布的(count、sum)、代数的(avg)、整体的(median)。
- OLAP 操作:
- 上卷:沿维层次汇总,如从月份汇总到季度。
- 下钻:细化到更细层次,如从季度下钻到月份。
- 切片:在一维上选择,如选 2023 年 Q1 数据。
- 切块:多维选择,如选 2023 年 Q1 且地区为华东的数据。
- 转轴:转换维的位置,如交换时间和地区维。
数据仓库设计与使用
- 设计框架:四视图(自顶向下选信息、数据源视图、数据仓库视图、商务查询视图)。
- 设计过程:选商务处理、确定粒度(如事务级)、选维、选度量。
- 开发方法:
- 自顶向下:整体设计,规范化高,周期长。
- 自底向上:从原型开始,灵活,易集成问题。
- 应用:
- 信息处理:查询、报表。
- 分析处理:多维分析,OLAP 操作。
- 数据挖掘:关联、分类等,与 OLAP 集成。
- OLAM:联机分析挖掘,结合 OLAP 和数据挖掘。
数据仓库实现
- 数据立方体计算:
- 全物化:计算所有方体,可能导致维灾难。
- 部分物化:选部分方体,如冰山立方体(仅存聚集值≥阈值的单元)。
- 索引技术:
- 位图索引:每位代表记录是否含某值,如性别维的 “男”“女” 位向量。
- 连接索引:物化关系连接,加速查询,如城市维与销售事实表的连接索引。
- 查询处理:确定操作对应 SQL,选择物化方体,如查询 {brand, province_or_state} 选含该维的物化方体。
- 服务器架构:
- ROLAP:用关系数据库,可扩展性好,性能较低。
- MOLAP:多维数组存储,性能高,空间需求大。
- HOLAP:混合,如底层关系、高层数组。
频繁模式挖掘及关联规则
基本概念
- 频繁模式:频繁出现在数据集中的模式,如项集、子序列等,动机是寻找数据内在规律,应用于购物篮分析、DNA 序列分析等。
- 项集相关定义项集:物品的集合,k – 项集包含 k 个物品,如 {牛奶,面包,尿布} 是 3 – 项集。
- 支持度计数:项集出现的频率,例如:{尿布,啤酒}同时出现的频率
- 支持度:包含项集的事务占比,例如:{尿布,啤酒}同时出现的概率
- 频繁项集:支持度≥最小支持度阈值的项集。
- 关联规则
- 形式为X → Y,如{牛奶, 尿布} → {啤酒}。
- 支持度:同时包含 X 和 Y 的事务占比,s(X → Y)=P(X U Y)。
- 置信度:包含 X 的事务中包含 Y 的占比,c(X → Y)=P(Y|X)=P(X U Y)/P(X)。
- 强规则:同时满足最小支持度和置信度阈值的规则。
通过支持度,置信度的方法非常暴力,运算量过大M = 2d,在大数据上没有办法运算
频繁项集挖掘方法
Apriori 算法
原理:利用先验性质(频繁项集的所有非空子集必频繁),若项集不频繁,其超集也不频繁(反单调)。
- 步骤
- 生成频繁 1 – 项集。
- 从频繁 k – 项集生成长度 k+1 的候选集,剪枝(删除含非频繁子集的候选)。
- 扫描数据库计数,保留支持度≥阈值的频繁项集,重复直至无新频繁项集。
e.g. 考虑以下数据,supmin=2,求频繁项集
| Tid | Items |
| 10 | A,C,D |
| 20 | B,C,E |
| 30 | A,B,C,E |
| 40 | B,E |
- 得出所有的1 – 项集:{A}{B}{C}{D}{E},支持度计数分别为2,3,3,1,3;{D}不频繁
- 接着得出所有的候选2 – 项集:{A,B}{A,C}{A,E}{B,C}{B,E}{C,E},支持度计数分别为1,2,1,2,3,2;{A,B}{A,E}不频繁
- 接着得出剩下的3 – 项集,{A,B,C}{A,B,E}{A,C,E}{B,C,E},支持度计数分别为1,1,1,2;{A,B,C}{A,B,E}{A,C,E}不频繁;然后一看肯定就没有4 – 项集
- 最后得出,所有的频繁项集(频繁的都放进来):{B,C,E}{A,C}{B,C}{B,E}{C,E}{A}{B}{C}{E}
问题:要对数据进行多次扫描;会产生大量的候选项集;对候选项集的支持度计算非常繁琐;
解决:减少对数据的扫描次数;缩小产生的候选项集;改进对候选项集的支持度计算方法;
优化方法
- 哈希表:映射项集到桶,淘汰低支持度桶中的项集。即通过频繁n项集产生n+1项集时,把n+1项都按照哈希值去散列,放到不同的桶里面,这样可以直接根据最小支持度划分。
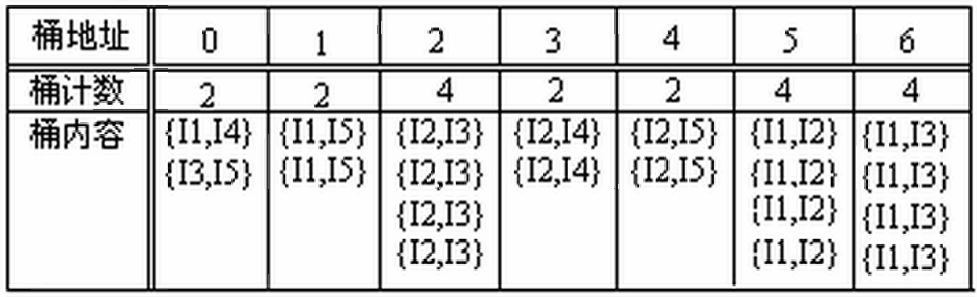
如过supmin=3,则只用考虑桶2,5,6中是否存在频繁项集(因为有可能多个映射到一个桶,但小于的肯定不存在频繁项集) - 划分:分块找局部频繁项集,两次扫描找全局频繁项集。
- D中的任何频繁项集必须作为局部频繁项集至少出现在一个部分中
- 第一次扫描:将数据划分为多个部分并找到局部频繁项集
- 第二次扫描:评估每个候选项集的实际支持度,以确定全局频繁项集
- 抽样:选择原始数据的一个样本,在样本上挖掘,验证并补全遗漏模式。
- 通过牺牲精确度来减少算法开销,为了提高效率,样本大小应该以可以放在内存中为宜,可以适当降低最小支持度来减少遗漏的频繁模式
- 事务压缩:删除不含频繁 k – 项集的事务。
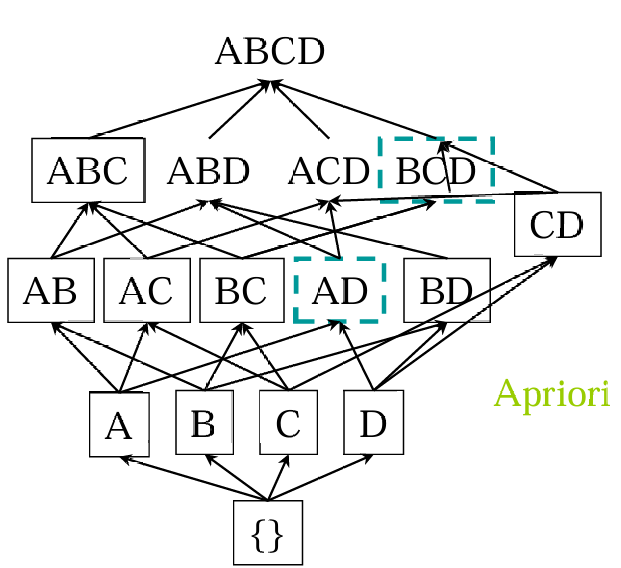
- 动态项集计数:所需要的数据库扫描比Apriori算法少。如下图,发现{A,D}是频繁的,则立刻开始计算{A,B,D},如果发现{A,B,D}是频繁的,则说明{A,B}、{B,D}是频繁的
FP-Growth 算法
- 原理:构建 FP 树压缩数据库,递归增长频繁模式,避免显式生成候选集。人话说,Apriori 相当于广搜,而FP-Growth相当于深搜,所以避免了产生候选项。
- 步骤:
扫描数据库,收集频繁项并排序,构建 FP 树。
从 FP 树头表每个项开始,构造条件模式基和条件 FP 树,递归挖掘。 - FP 树优势:完整性(保存完整信息)、紧凑性(频繁项排序共享结点,删除非频繁项)。
e.g.考虑以下数据
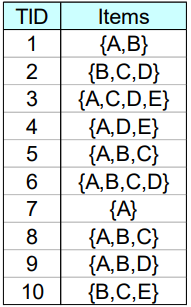
先1-项集计数,然后递减排序,得到右图
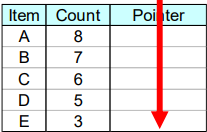
接着遍历事物1-10,按照1-项集计数顺序来排列节点,然后构造FP-Tree
读取TID=1的事务后
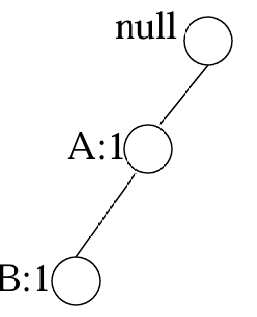
读取TID=2的事务后
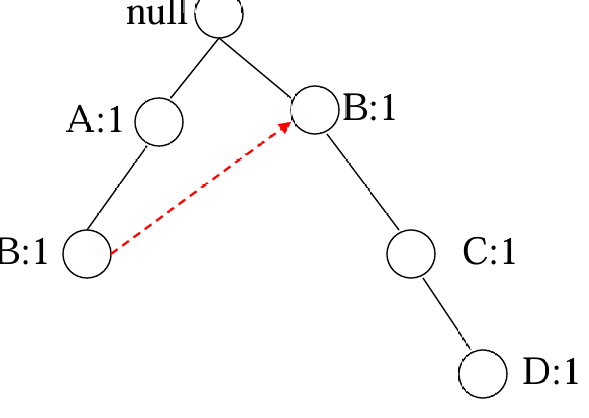
最后,读取全部事物后,可以得到:
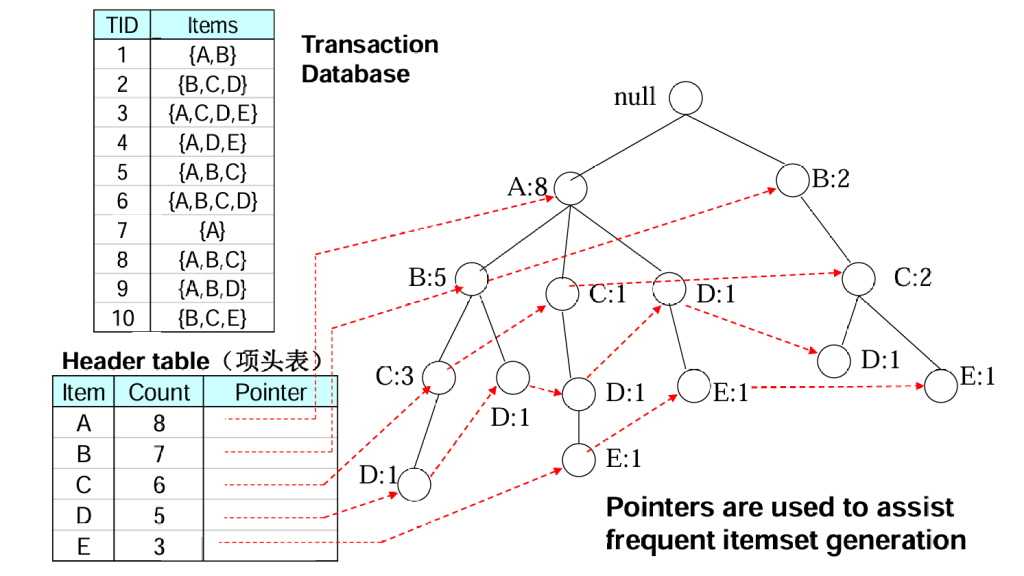
通常来说FP树的大小比未压缩的数据小,因为购物篮数据的事务常常共享一些共同项
在最好情况下,所有的事务都具有相同的项集,FP树只包含一条结点路径
在最坏情况下,所有的事务都具有唯一项集,由于事务不包含任何共同项,FP树的大小实际上与原数据的大小一样,然而,由于需要附加的空间为每个项存放结点间的指针和计数,FP树的存储需求增大
如果颠倒前面的排序,按照支持度从小到大排序。那么可见FP树明显大了很多。
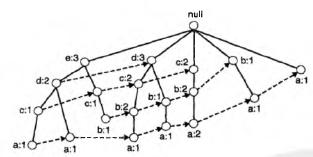
但是!支持度计数递减序并非总是导致最小的树,有可能也会反过来,总之就是不一定
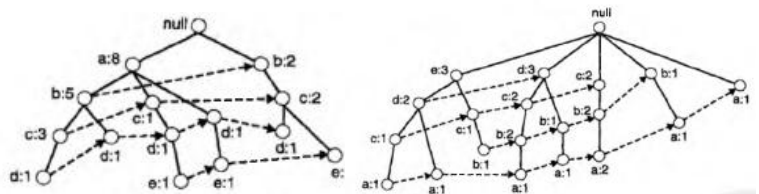
通过FP-Tree找频繁项集
首先分别找到以ABCDE结尾的频繁项集(通过虚线代表的指针)
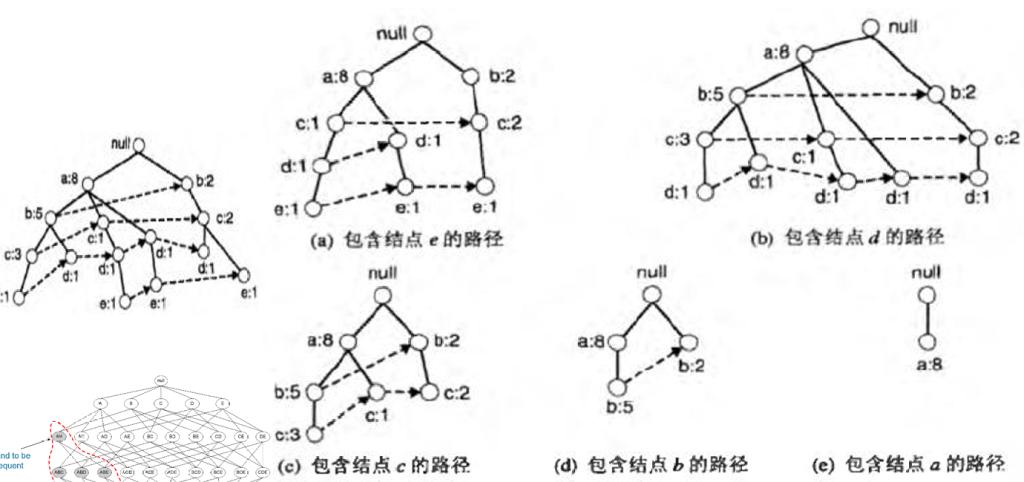
- 收集包含E结点的所有路径,这些初始路径称为前缀路径[a]
- 由E的前缀路径,把与结点E相关联的支持度计数相加得到E的支持度计数为3,则{E}是频繁项集(假设最小支持度为2)
- 由于E是频繁的,因此算法必须解决发现以DE、CE、BE、AE结尾的频繁项集的子问题。在解决这些子问题之前,必须先将前缀路径转化为条件FP树[a->b]
- FP增长使用E的条件FP树来解决发现以DE、CE、BE、AE结尾的频繁项集的子问题
- 通过d的计数,可以得到{d,e}是频繁项集,于是可以计算下一个子问题:{a,d,e}和{c,d,e}是不是频繁项集。因为de条件FP树只包含一个支持度等于最小支持度的项A,所以我们不用再考虑cde了
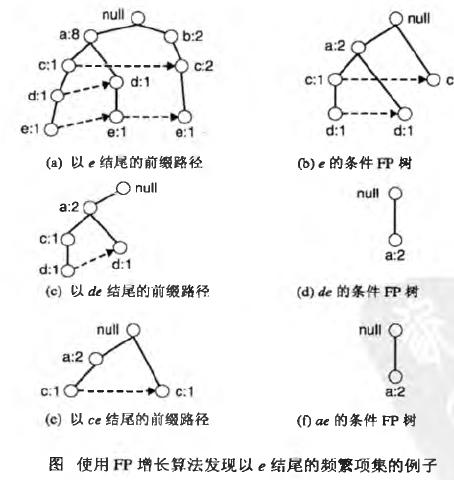
如何从前缀路径转化为条件FP-Tree呢?
以上面的 (a) -> (b) 为例,
1)首先,必须更新前缀路径上的支持度计数,因为某些计数包括那些不含项E的事务。图(a)中B:2-C:2-E:1包括不含E的事务{B,C},必须将该前缀路径上的计数调整为1,以反映包含{B,C,E} 事务实际个数
2)删除E结点,修剪前缀路径。删除E结点是因为,沿这些前缀路径的支持度计数已经更新,已反映包含E的那些事务,并且发现以DE、CE、BE、AE结尾的频繁项集的子问题不再需要结点E的信息
3)更新沿前缀路径上的支持度计数之后,某些项可能不再是频繁的。例如,结点B只出现 1次,它的支持度计数等于1,即只有一个事务同时包含B 和E,因而所有以BE结尾的项集一定都是非频繁的,所以在其后的分析中可以忽略B
4)E的条件FP树如图b,该树看上去与原来的前缀路径不同,因为频度计数已经更新,并且结点B和E已被删除
ECLAT 算法
- 原理:将水平数据转换为垂直数据格式,项集对应 TID 集合,通过交集计算支持度。
- 步骤:转换数据为垂直格式,对 k – 项集计算 TID 集交集,得到 k+1 – 项集支持度。
优点:在产生候选(k + 1)项集时利用先验性质;不需要扫描数据库来确定(k + 1)项 集的支持度(k+1),因为每个k项集的集携带了计 算支持度的完整信息
缺点:TID集可能很长,需要大量内存空间,长集合的交 运算还需要大量的计算时间
关联规则的评估
支持度 – 置信度框架局限性:强规则可能误导,如购买计算机游戏→购买录像,支持度 40%,置信度 66%,但实际购买录像概率 75% 更高,两者负相关。
因此需要引入新的相关性度量指标扩充
提升度lift
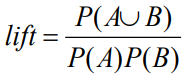
>1 正相关,=1 独立,<1 负相关。
考虑这种情况,
| 打篮球 | 不打篮球 | 总计 | |
| 吃谷物 | 2000 | 1750 | 3750 |
| 不吃谷物 | 1000 | 250 | 1250 |
| 总计 | 3000 | 2000 | 5000 |
计算提升度后得到,P(B)为打篮球,P(C)为吃谷物,那么得到打篮球不吃谷物更加可信。尽管他的支持度/置信度更低

卡方检测
如何计算呢?先根据sum得到两类人群比例,再往回填上每一类人的预期个数
| 打篮球 | 不打篮球 | 总计 | |
| 吃谷物 | 2000(2250) | 1750(1500) | 3750 |
| 不吃谷物 | 1000(750) | 250(500) | 1250 |
| 总计 | 3000 | 2000 | 5000 |
那么,通过卡方检测,O为观察值,E为理论值
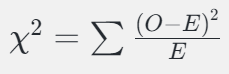
Χ2=(2250-2000)2/2250+(1750-1500)2/1500+(1000-750)2/750+(250-500)2/500=277
通过查表,在显著水平 α = 0.01水平下,计算得到的Χ2=277 >>10.828,说明打篮球与是否吃谷物之间存在显著关系(哪种关系先别管,反正有关系,不然统计量应该没有关联)。
其他度量:Yule’s Q、Mutual Information、J-Measure 等。
总结算法对比
| 算法 | 核心特点 | 优势 | 劣势 |
|---|---|---|---|
| Apriori | 候选生成 – 测试,先验剪枝 | 原理简单,易实现 | 多次扫描,候选集多 |
| FP-Growth | 构建 FP 树,递归挖掘 | 少扫描,无候选集 | 树构建复杂,内存需求 |
| ECLAT | 垂直数据,TID 集交集 | 支持度计算高效 | TID 集长,交运算耗时 |
分类
定义:给定训练集,每个记录为 (x,y) 元组,x 是属性集,y 是类标号,任务是学习模型将 x 映射到预定义 y。
具体示例:邮件分类(识别垃圾邮箱),肿瘤识别(良性恶性)
通用框架:训练阶段(训练模型)->测试阶段(测试模型)
决策树分类
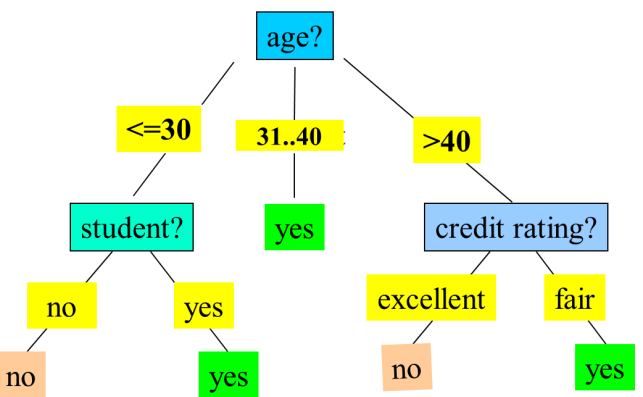
单节点的不纯性度量
如何构建呢?按照下面的来,使用HUNT算法
- 属性测试条件表示:
- 标称属性:多路划分或二元划分。
- 序数属性:保持顺序的二元划分。
- 连续属性:二元划分或离散化。
- 分裂属性选择:基于不纯性度量,如基尼指数、信息熵、分类误差。
- 停止划分时机:节点样本同类别或属性用尽。
不纯性度量有三个指标,我们选择时候纯净(pure)度大的,这样更好的区分开了数据。
- 基尼指数:Gini(t)=1-∑ p(j|t)2,值越小节点越纯。p(j|t)为节点t中样本测试输出取类别j的概率
- 信息熵:H(S) = Entropy(S)=-∑ p(j|t) log2(p(j|t)),熵越小分布越纯。
- 分类误差:CE(t) = Error(t)=1- max p(i|t),CE越小,说明样本越集中在某一侧,则越纯
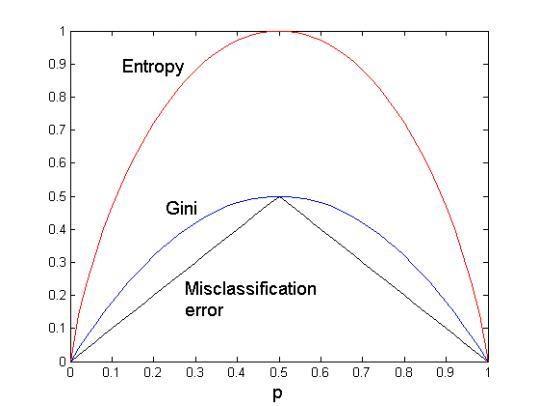
可以看到三个不纯度都是一致的,单调性一样。
子节点的集合不纯性
对子结点的不纯性度量进行加权求和得到
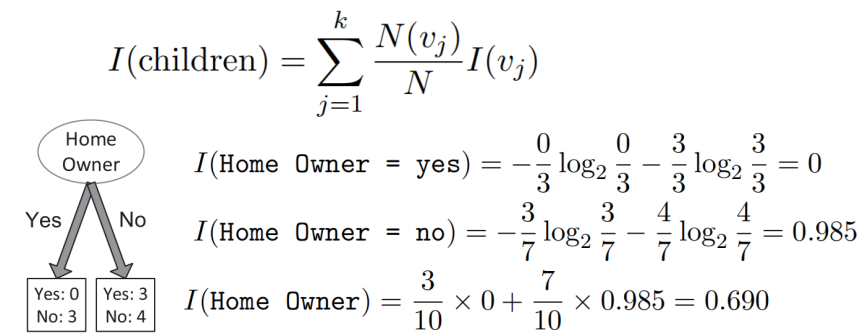
信息增益
用属性A划分样本集S,划分前样本数据集的不纯程度(熵)和划分后样本集的不纯程度(熵)的差值
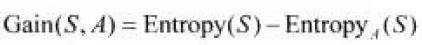
按属性A划分S后的样本子集S1,S2,…,Sk的熵定义:
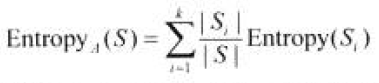
信息增益越大越纯粹,越有利于分类。
增益率
熵和基尼指数等不纯性度量存在一个潜在的局限,即更容易选择具有大量不同值的定性属性,导致更精细的划分(比如说我这里属性划分按照<1<9 else,其他地方划分<2 <5 <6 < 7 else,这样很容易局部过拟合了)。
解决要么是仅生成二元决策树(避免使用不同数目划分),要么就是修改划分标准以考虑属性生成的划分数量,即使用称为增益率(gain ratio)的度量来补偿产生大量子结点的属性
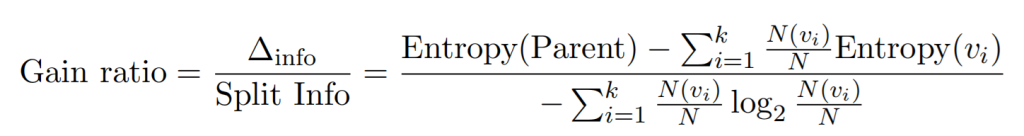
- Gain(A) 是属性 A 的信息增益,即划分前后的熵差。
- SplitInfo(A) 衡量属性 A 的分裂能力,k是属性 A 的取值个数,N(vi)是属性A取值为第i类的样本子集,N是总样本数
对于每个候选属性都可以计算Gain(A),取最大的计算增益率是否也是最大,最后取增益率最大的作为真正的分裂属性。
经典算法
| 算法 | 属性选择度量 | 特点 |
|---|---|---|
| CART | 基尼指数 | 生成二叉树,处理连续和标称属性 |
| ID3 | 信息增益 | 处理离散属性,易偏向多值属性 |
| C4.5 | 信息增益率 | 处理连续属性和缺失值,生成规则(简单易解释准确率高,缺点多次扫描排序低效) |
做题
做题参考前面数据变换与数据离散化的决策树,套用不同的不纯度公式即可
模型过拟合与选择
- 过拟合:模型复杂捕捉训练集噪声,测试错误率上升,如决策树规模过大时训练错误率为 0 但测试错误率上升。
- 模型选择
- 验证集应用:划分训练集为训练和验证子集(未被训练),选验证错误率最低模型。
- 复杂度合并:泛化错误率 = 训练错误率 +α× 复杂度,α 为超参数。让模型不仅要考虑训练错误率,还要考虑模型的复杂度
- 统计范围估计:PPT不见了
模型评估
讨论估计模型泛化性能的方法,即跑一下没训练的测试集效果
评估指标
混淆矩阵(Confusion Matrix)
- 二元分类:直观展示了评估准确性
| 真实类别 \ 预测类别 | 正类(Yes) | 负类(No) |
|---|---|---|
| 正类(Yes) | 真阳性(TP) | 假阴性(FN) |
| 负类(No) | 假阳性(FP) | 真阴性(TN) |
- 准确率(Accuracy):正确分类的样本占比,Accuracy = (TP+TN)/(TP+TN+FP+FN)。
- 错误率(Error Rate):Error Rate = (FP+FN)/(TP+TN+FP+FN) = 1 – Accuracy。
- 灵敏度(Sensitivity):正类样本被正确识别的比例,Sensitivity = TP/(TP+FN)(又称召回率,Recall)。
- 特异性(Specificity):负类样本被正确识别的比例,Specificity = TN/(TN+FP)。
- 精度(Precision):预测为正类的样本中实际为正类的比例,Precision = TP/(TP+FP)。
- F1 分数:精度和召回率的调和平均,F1=(2 * Precision * Recall)/(Precision + Recall)
- Fß分数:精度和召回率的加权度量,Fß=((1+ ß2)* Precision * Recall)/( ß2 * Precision + Recall)
ROC 曲线与 AUC
- ROC 曲线:横轴为假阳性率FPR,纵轴为真阳性率TPR,曲线越靠近左上角,模型性能越好。
- AUC(曲线下面积):AUC=1 表示完美分类器,AUC=0.5 表示随机猜测。
评估方法
- 保持方法:随机划分训练集和测试集,如 2/3 训练、1/3 测试
- 交叉验证:k 重交叉验证,如 10 折交叉验证,每个实例测试 1 次、训练 k-1 次。
超参数使用
泛化错误率 = 训练错误率 +α× 复杂度,α 为超参数。让模型不仅要考虑训练错误率,还要考虑模型的复杂度
注意事项
- 训练集与测试集重叠:若测试集包含训练数据,会高估模型性能,需确保数据完全独立。
- 误用验证错误率:验证集用于模型选择后,其错误率会低估真实泛化误差,需用独立测试集最终评估。
模型比较
MA在30大小测试集上的准确率为85%,MB在5000大小测试集上准确率为75%,MA就是好模型吗?
自然不一定,一是测试集大小不一致,涉及到置信区间的估计;二是因为是不同的测试集,涉及到观测偏差统计显著性的测试
提高分类准确率的技术
- 装袋(Bagging):有放回抽样生成多个训练集,训练多个模型,投票决定结果
- 算法:生成 k 个 bootstrap 样本,每个都分别训练模型,多数表决分类(在回归任务平均值预测)。
- 提升(Boosting):迭代调整样本权重,误分类样本权重增加,最终加权投票。
Adaboost:初始权重相等,根据错误率计算模型权重log[(1-error)/error]。 - 随机森林:构建多棵决策树,每棵树随机选择属性子集,分类时,每棵树都投票并返回得票最多的类,相比Adaboost 对错误和离群点鲁棒性更好。
- 可以选择 装袋 与 随机属性选择组合
基于规则的分类
- 规则表示与评估
- 采用 IF-THEN 规则,如
R1:IF(age=youth)AND(student=yes)THEN(buys_computer=yes)。 - 评估指标:
- 覆盖率
coverage(R)=ncovers/|D|,表示规则覆盖(满足前提)的元组数占训练集比例。 - 准确度
accuracy(R)=ncorrect/ncovers,表示规则正确分类的元组占覆盖元组的比例。
- 覆盖率
- 采用 IF-THEN 规则,如
- 规则冲突与默认处理
- 冲突解决策略:(不同规则之间肯呢个会有冲突,解决方法)
- 规模序:优先选择属性测试最多的规则。
- 基于类的规则序:按类的普遍性或误分类代价排序。
- 基于规则的规则序:按准确度、覆盖率排序成决策表。
- 默认类:当无规则覆盖时,选择多数类或未覆盖元组的多数类,如默认规则
IF THEN class=多数类。
- 冲突解决策略:(不同规则之间肯呢个会有冲突,解决方法)
- 规则提取与归纳
- 从决策树提取:每条根到叶路径生成一条规则,规则间互斥且穷举,如
age=young AND student=no → buys_computer=no等。 - 顺序覆盖算法(如 FOIL):从训练数据直接学
- 步骤:一次学习一条规则,删除覆盖元组,重复至满足条件。
- 规则生成:从空规则开始,贪心添加属性测试,用准确率、熵、FOIL 信息增益
FOIL_Gain=pos'*(log2(pos'/(pos'+neg')-log2(pos/(pos+neg)))评估。 - 剪枝:如 FOIL 剪枝
(pos-neg)/(pos+neg),提升泛化能力。
- 从决策树提取:每条根到叶路径生成一条规则,规则间互斥且穷举,如
贝叶斯分类
- 公式:P(H|X)=P(X|H)P(H)/P(X),其中P(H)为先验概率,P(X|H)为似然度,P(H|X)为后验概率。
- 例子:X=(age<=30,income=medium,student=yes,credit_rating=fair),计算属于buys_computer=yes的概率
- 套用条件概率公式,计算:
- P(Ci ):即P(buys_computer = “yes”)或no的概率
- P(X|Ci ):在yes或no的条件下,X发生的概率,概率认为是这四个直接乘
- 最后那个概率大,就选哪个
- 套用条件概率公式,计算:
一些基本假设与处理
- 假设属性条件独立:
P(X|Ci)=∏P(xk|Ci)。 - 连续属性:
- 离散化:分区间计算比例。
- 正态分布:
P(xk|Ci)≈g(xk,μCi,σCi)=1/(√(2π)σCi)e^(-(x-μCi)²/(2σCi²))。
- 零概率解决:拉普拉斯校准,如
income=low原计数 0,校准后Prob=(0+1)/(1000+3)=1/1003。
神经网络与 BP 算法
多层前馈网络:输入层、隐藏层、输出层,神经元通过权重wij和偏倚θj连接,输出用 S 型函数Oj=1/(1+e^(-Ij)),其中Ij=∑xiwij+θj。
BP算法步骤:
- 前向传播:
- 在前向传播过程中,输入数据从输入层经过隐藏层传递到输出层,计算出模型的预测值 ypred和损失值 L。
- 反向传播:
- 根据链式法则(用于处理复合函数求导的重要规则),计算损失函数相对于每个参数的梯度 ∂L/∂w,从输出层向输入层逐层反向传播。
- 参数更新:
- 利用梯度下降等优化算法,通过梯度信息更新每层的权重和偏置:w=w−η⋅∂w/∂L,其中w为参数,η为学习率
示例:

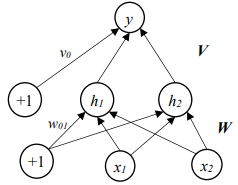
前向传播
要计算前向传播,就需要算出实际的a1,a2,然后按照要求使用激活函数得出隐藏层h1h2。
做题就是按照公式组合,比如说第一个可以看到h1是由x1,x2,w0,W共同组合成,因此我们就可以先计算出a1,然后激活后作为h1,同理,对于y,由h1,h2,v0,V这个组成,还是组合后激活得到y
解答:



反向传播
使用第 4 个样本 (x = [0.7, 0.6],t = 1),基于交叉熵损失函数计算每个参数的偏导数
解答:
通过查询可知,交叉熵损失函数L = −tlog y − (1 − t)log(1 − y),因为t=1,所以L=-logy

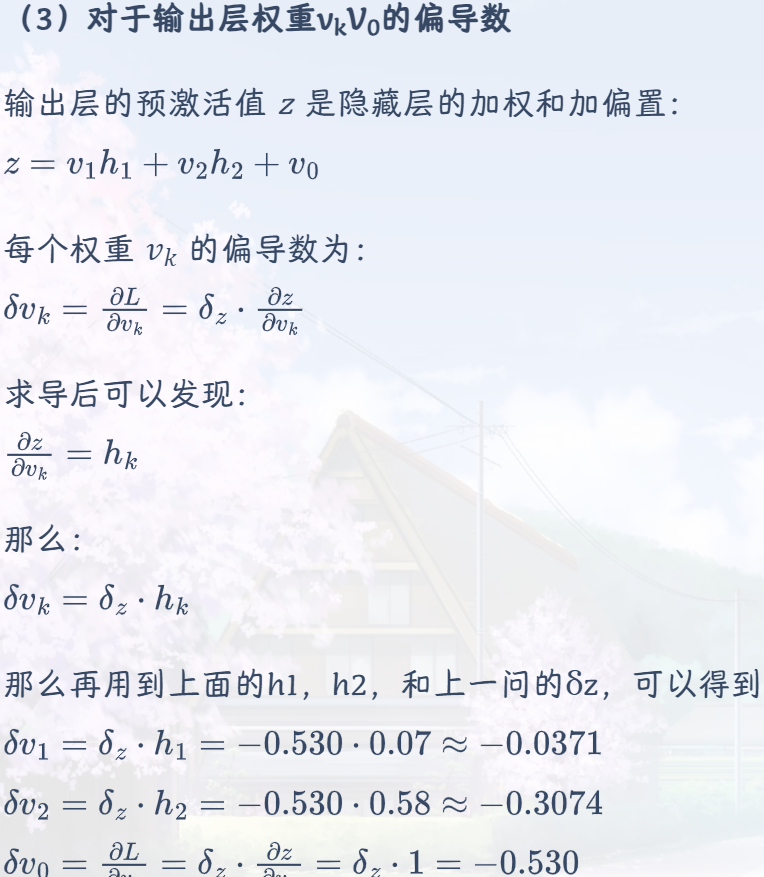
后续类似不再赘述,最后权重的更新按照学习率和初始参数w=w−η⋅∂w/∂L,计算得到最后的
支持向量机 (SVM)
- 基本原理
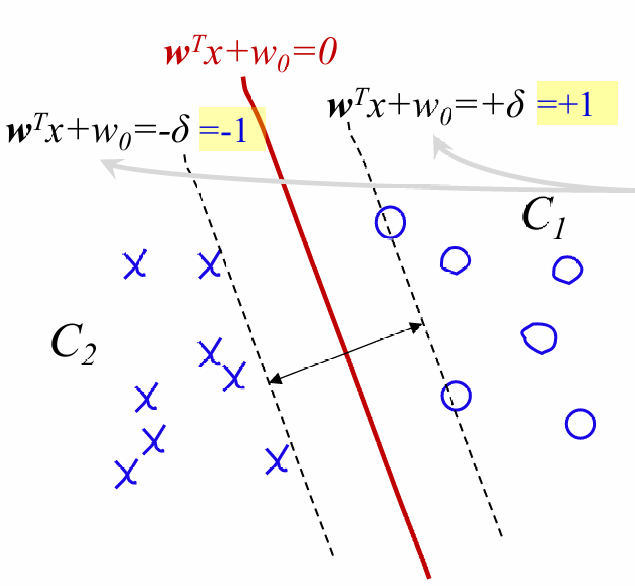
- 线性可分:找最大间隔超平面
f(x)=wx+b,非线性通过核函数映射到高维,如(x1,x2)→(x1²,√2x1x2,x2²)。
- 线性可分:找最大间隔超平面
- 与神经网络对比
- SVM 基于统计学习理论,结构风险最小化,理论更严谨;NN 依赖工程技巧,易陷入局部最小。
集成学习
| 方法 | 核心思想 | 特点 |
|---|---|---|
| Bagging | 有放回抽样生成 k 个训练集,基分类器投票 | 减少方差,对噪声鲁棒 |
| Boosting | 迭代调整样本权重,聚焦错分样本,基分类器加权投票 | 减少偏差,对离群点敏感 |
| 随机森林 | 组合决策树,随机选择属性子集分裂 | 抗噪声,泛化能力强 |
其他分类方法
频繁模式分类
用频繁模式生成关联规则分类,如IF income=high THEN buys_computer=yes。
惰性学习法
KNN:找 k 个最近邻,多数表决,如 k=5,用欧氏距离d=√∑(xi-xj)²。
CBR:基于案例推理,如汽车故障诊断,匹配相似案例解决方案。
其它的其它方法
其他方法:
遗传算法(模拟进化,如选择、交叉、变异来不断优化)
模糊集(处理模糊概念实现高层次抽象,如 “高收入” 隶属度 0.96)
粗糙集(处理不精确数据,通过上下近似集定义(无法确认就放在边界))。
聚类
是什么?将数据对象划分为子集(簇)的过程,要求簇内对象相似,簇间相异,属于无监督学习,无需类标号信息。
应用:
空间数据分析:创建 GIS 主题映射、探测空间簇。
图像模式识别:对手写数字聚类提高识别准确率。
经济学:客户分组以优化客户关系管理。
Web 关键词搜索:将搜索结果分组便于呈现。
什么样的聚类是好的?最大化类内相似性,最小化类间相似性,依赖相似性度量的选择。
主要方法比较
| 方法类型 | 核心思想 | 代表算法 | 优点 | 缺点 |
|---|---|---|---|---|
| 划分方法 | 将数据集划分为 k 个互斥簇,基于距离迭代优化 | K – 均值、K – 中心点(PAM) | K – 均值复杂度低,PAM 抗离群点 | K – 均值需预设 k,对初始值敏感;PAM 计算代价高 |
| 层次方法 | 创建数据的层次分解,分凝聚式和分裂式 | AGNES(凝聚)、DIANA(分裂) | 无需预设簇数,可集成其他技术 | 无法撤销操作,伸缩性差(O (n²)) |
| 基于密度方法 | 基于密度相连定义簇,发现任意形状簇 | DBSCAN、OPTICS | 抗噪声,能发现任意形状簇 | 参数 Eps 和 MinPts 难以确定 |
| 基于网格方法 | 将空间量化为网格,在网格上操作 | STING、CLIQUE | 处理速度快,独立于数据量 | 高维时网格数指数增长,矩形网格精度低 |
划分方法
- K – means算法
- 步骤:随机选 k 个初始簇中心,分配对象到最近簇,更新中心(用上次分配到这个簇所有对象的均值作为中心),重复至稳定。
- 目标函数:误差平方和 E=∑∑dist (p,ci)²,ci 为簇均值。
- 优点:复杂度O(tkn);其中n 是对象的数目, k 是簇的数目, t 是迭代的次数. 通常k、t << n
- 缺点:要事先知道nk,初始值敏感,离群点敏感,噪声敏感,不适合凸面
- 变种:K – 众数处理标称属性,用众数代替均值(在无法获取平均值时候)。
- K – medoids(PAM)
- 核心:用实际对象(中心点)代表簇,最小化绝对误差和 E=∑∑dist (p,oi),oi 为中心点。下面这个先找到中心点,然后去找最近的事件对象代表中心。
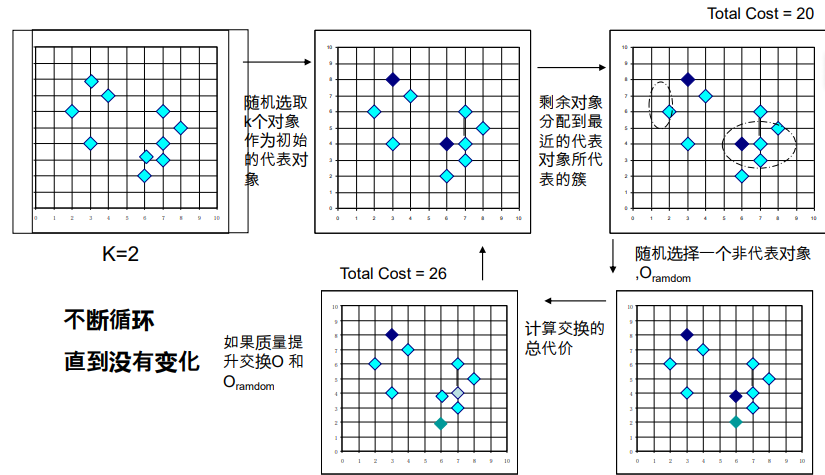
- 缺点:NP-hard问题,大数据代价很高
- 改进:CLARA(抽样改进 PAM)、CLARANS(随机搜索改进)。
- 核心:用实际对象(中心点)代表簇,最小化绝对误差和 E=∑∑dist (p,oi),oi 为中心点。下面这个先找到中心点,然后去找最近的事件对象代表中心。
层次方法
- 凝聚式(AGNES)
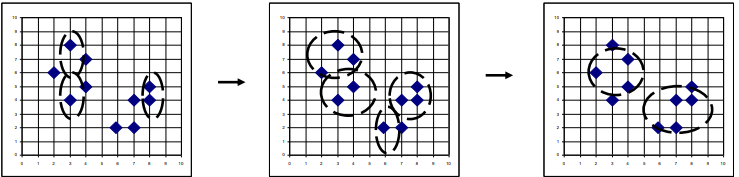
- 过程:初始每个对象为一簇,逐步合并相近簇,直至满足条件。
- 簇间距离度量:最小距离(单连接)、最大距离(全连接)、均值距离、平均距离。
- 分裂式(DIANA)
- 过程:初始所有对象在一簇,逐步分裂直至每个对象自成一簇。
基于密度方法详解(DBSCAN)
- 概念:
- Eps:邻域半径,MinPts:邻域最小点数。
- 核心对象:Eps 邻域含≥MinPts 个点。
- 直接密度可达、密度可达、密度相连。
- 算法步骤:标记未访问点,选核心对象扩展簇,处理边界点和噪声点。
- 参数确定:通过 k – 距离图确定 Eps 和 MinPts,k=4 为经验值。
- 原理:依赖簇的基于密度的思想:它定义簇为密度相连的点的最大集合
基于网格方法详解(STING)
- 原理:将空间划分为多层网格,存储各层单元统计信息(计数、均值、标准差等)。
- 步骤:定义网格,分配对象,计算密度,删除低密度单元,合并稠密单元成簇。
- 优缺点:查询快(O (K)),只需为非空单元创建网格;但簇形状受网格限制,精度低,无法捕捉类似椭圆边界密度,对高维数据效果很差。
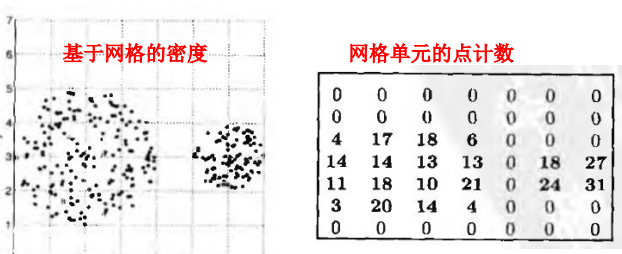
聚类评估方法
- 聚类趋势评估
- 霍普金斯统计量 H=∑yi/(∑xi+∑yi),H≈0.5 表示均匀分布,H→0 表示存在聚类结构。
- 簇数确定
- 经验公式:k≈√n/2(n 为数据点数)。
- 肘方法:绘制簇内方差 – 簇数曲线,取拐点。
- 交叉验证:划分数据集,用部分建立模型,检验集评估。
- 质量测定
- 外在方法:与基准比较,如 Bcubed 精度(同一簇中同类别对象比例)和召回率(同类别对象同簇比例)。
- 内在方法:轮廓系数,衡量簇的紧凑性和分离性,范围 [-1,1],越接近 1 越好。
推荐系统及社会网络
推荐系统
为什么有这东西?因为信息太多了,需要快速便捷找到可能需要的内容
主要类型
| 类型 | 核心思想 | 优点 | 缺点 |
|---|---|---|---|
| 基于内容 | 根据物品属性(如类型、颜色)和用户偏好匹配 | 不依赖其他用户数据,适合冷启动 | 需准确描述物品内容,难以发现新兴趣 |
| 协同过滤 | 依赖 “相似用户喜欢相似物品” 假设 | 可发现用户潜在兴趣,无需物品内容 | 数据稀疏时效果差,存在冷启动问题(新物品无用户交互) |
| 用户 – 用户 CF(协同过滤的一种方法) | 找与目标用户相似的 N 个用户,基于其行为推荐 | 可解释性好 | 大规模计算效率低,用户相似度计算复杂 |
| 物品 – 物品 CF(协同过滤的一种方法) | 找与目标物品相似的物品,基于用户对相似物品的评分推荐 | 稳定性高,适合电商 | 新物品难以推荐 |
协同过滤实现
首先需要有评价表,表示user对于物品的打分
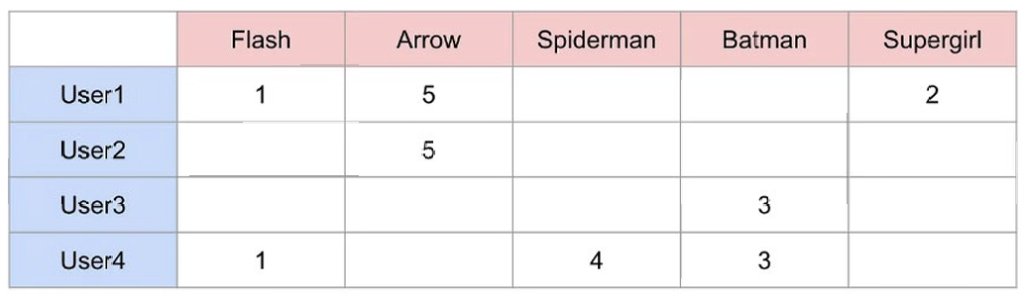
User-User CF
- 步骤 1:计算用户间相似度
- 思想:把用户评分作为高维向量,再通过计算相似性(如余弦相似度,Jaccard相似度,皮尔逊相关系数)
- e.g.用户 User1 的评分向量为[1, 5, 0, 0, 2],用户 User2 为[0, 5, 0, 0, 0],代入公式(sim(u,v)=u·v/(||u|| · ||v||))可得两者的余弦相似度为 0.91
- 步骤 2:寻找 k 个相似用户(k-NN)
- 按照相似度,找k个相似度最高的用户作为邻居
- 步骤 3:预测目标用户的评分
- 未加权:对这些邻居对某一物品的评分平均值
- 加权平均:借助相似度加权
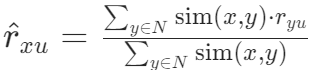
- 标准化处理:为避免用户评分尺度差异(如有人偏爱打高分),可先对评分进行标准化:r’ = r – avg(r),预测后再还原。
- 步骤 4:生成推荐列表
- 排序,对于用户没交互的物品,预测评分并降序排列,选取TOP-N推荐
Item-Item CF
思路和与 User-User CF 类似,但将相似度计算对象从用户改为物品。
优势:相比 User-User CF,Item-Item CF 更稳定,适合电商等物品数远少于用户数的场景。
推荐系统的评估指标
- 预测准确度
- RMSE(均方根误差):
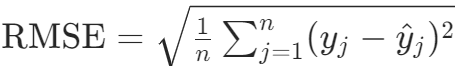 ,例如预测评分与实际评分的偏差平方和的平方根。
,例如预测评分与实际评分的偏差平方和的平方根。 - MAE(平均绝对误差):
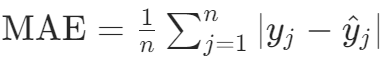 ,衡量预测评分与实际评分的平均绝对偏差。
,衡量预测评分与实际评分的平均绝对偏差。
- RMSE(均方根误差):
- TopN 推荐指标
- 准确率(Precision):推荐列表中相关物品的比例。
- 召回率(Recall):测试集中相关物品被推荐的比例。
- F1 Score:F1=(2 * Precision * Recall)/(Precision + Recall),平衡准确率和召回率。
- 其他指标
- 平均排名倒数(MRR):
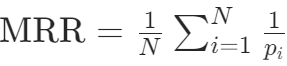 ,确定所找到的item放的位置好不好。
,确定所找到的item放的位置好不好。 - 累计增益(Cumulative Gain,CG):衡量推荐列表中所有相关物品的相关性分数总和,不考虑物品在列表中的位置顺序,CG=SUM(reli)
- 若推荐列表中物品的相关性分数为 [3, 2, 3, 0, 1, 2],CG= 3 + 2 + 3 + 0 + 1 + 2 = 11。
- 局限性:未考虑用户更关注推荐列表靠前的物品,无法反映排序的优劣。
- 折扣累计增益(Discounted Cumulative Gain,DCG):在 CG 的基础上,对推荐列表中靠前的物品赋予更高权重,体现位置的重要性(越靠前的物品对用户影响越大)。
- 标准公式:
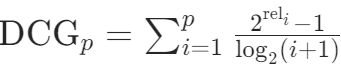 i表示第几个位置,reli表示相关性评分,2reli用来放大差异
i表示第几个位置,reli表示相关性评分,2reli用来放大差异 - 作用:通过折扣因子惩罚靠后位置的物品,更符合用户实际浏览习惯(优先关注前排推荐)。
- 标准公式:
- 标准化折扣累计增益(Normalized Discounted Cumulative Gain,NDCG)
- 将 DCG 与 “理想情况下的 DCG(IDCG)” 相除,得到 0 到 1 之间的标准化值,用于比较不同推荐列表的质量。
- NDCG = DCG / IDCG
- 作用:消除不同推荐列表长度和相关性分布的影响,便于跨用户、跨模型的性能对比。
- 平均排名倒数(MRR):
推荐系统面临的挑战
- 长尾问题:物品流行度和用户活跃度呈长尾分布,热门头部物品样本多,模型学习效果好,长尾物品样本少,推荐效果差。
- 马太效应:模型倾向于给热门物品更高评分,推荐频率超过其受欢迎程度,形成 “热门更热” 的闭环。
- 稀疏性问题:效用矩阵规模大且极度稀疏,如 10000 个用户 ×10000 个物品,仅有 10000 个评分,稀疏性达 99.9999%,导致协同过滤失效,机器学习模型易过拟合。
- 冷启动问题:新用户无行为数据,新物品无用户交互,依赖大量用户行为的算法无法训练模型。
社会网络
- 定义:由节点(个人 / 组织)和边(关系)构成的网络结构,关系可为朋友、亲属等。
- 表示方法:
- 图方法:节点为顶点,边为连接。
- 邻接矩阵:无向网络矩阵对称,有向网络如 Twitter 关注关系矩阵不对称。
社会网络的关键特性
- 小世界效应:最多只需要6个陌生人就可以和任何一个人认识
- 六度分离理论:Travers 和 Milgram 实验发现美国人平均路径长 5.5,MSN 网络 1.8 亿节点实验得平均路径长 6.6。
- 社区结构:
- 聚类系数:衡量朋友的朋友成为朋友的概率,公式为
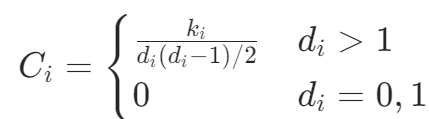 ,其中ki为邻居间边数,di为邻居数
,其中ki为邻居间边数,di为邻居数
- 聚类系数:衡量朋友的朋友成为朋友的概率,公式为
- 网络直径:网络中所有节点对的最小路径长度的最大值,反映网络的 “最大距离”。
社区发现方法分类
| 方法类型 | 核心思想 | 典型算法 / 示例 | 特点 |
|---|---|---|---|
| 以节点为中心 | 基于完全子图(团) | 团过滤CPM 算法:枚举 k 规模团,共享 k-1 节点的团构成社区 | k=3 时,团 {1,2,3} 与 {1,3,4} 共享 2 节点,属同一社区;NP-hard问题 |
| 以群组为中心 | 基于子图密度 | 准团:允许部分节点低连通性,γ=1 时为团 | 优化局部密度,适应大规模网络 |
| 以网络为中心 | 基于整体拓扑结构 | 相似性度量(Jaccard、余弦)、隐含空间模型 | 节点映射到低维空间,用 K 均值聚类 |
| 以层次为中心 | 层次化分解或聚合 | 分裂式:删边介数高的边,一旦断开就可以认为两个新社区;聚合式:基于模块度合并 | 模块度Q>0.3 质量好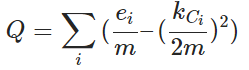 m图中边总数, m图中边总数,对每个社区 i: ei:社区 i 中的内部边的数量 kCi:社区 i 中所有节点的度数之和 |
具体示例:
CMP
示例:k=3 时的社区发现
- 步骤 1:枚举 k=3 的团
- 从网络中找出所有规模为 3 的团,例如:
- {1,2,3}、{1,3,4}、{4,5,6}、{5,6,7}、{5,6,8}、{5,7,8}、{6,7,8} 。
- 步骤 2:构建团图并合并社区
- 若两团共享 k-1=2 个节点,则视为邻接。例如:
- 团 {1,2,3} 与 {1,3,4} 共享节点 {1,3},合并为社区 {1,2,3,4};
- 团 {4,5,6} 与 {5,6,7} 共享 {5,6},逐步合并为 {4,5,6,7,8} 。
- 最终社区
- {1,2,3,4} 和 {4,5,6,7,8} 。
准团(γ- 密度子图)
定义:当 γ=1 时,准团要求子图中每个节点的度数至少为 (γ×(子图节点数 – 1)),即完全子图(团)。
示例:下图 {4,5,6,7,8} 是 5 节点的团,任意两节点间均有边,满足 γ=1 的准团定义 。
基于相似性度量的聚类
Jaccard=|A∩B| / |A∪B|
以层次为中心的社区发现
参照公式
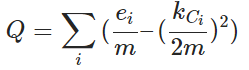
对于如下社区,有13 个节点分为 3 个社区,边数 23 条。ei:社区 i 中的内部边的数量;kCi:社区 i 中所有节点的度数之和
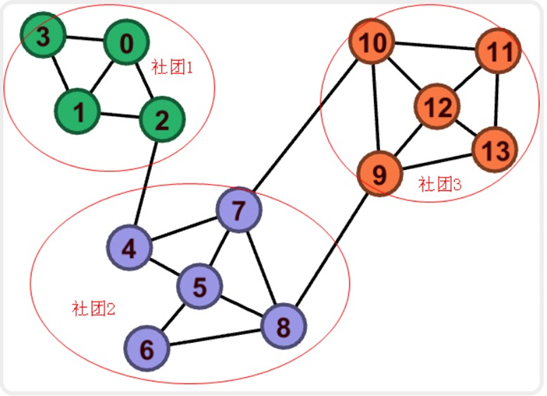
最终结果,Q>0.3,可以认为社区划分良好