黑盒测试与白盒测试

• 黑盒测试
  • 根据程序外部特征进行测试，不关心内部实现和逻辑结构
    • 关注输入和输出，忽略代码内部逻辑。
    • 基于需求文档和功能说明书设计测试。
    • 测试人员无需具备编程知识。
  • 常用方法：
    • 等价类划分： 将输入数据分为等价类，减少测试用例。
    • 边界值分析： 测试数据的边界值（如最大值、最小值）。
    • 决策表测试： 列举条件与结果关系，设计测试用例。
    • 随机测试： 随机生成输入数据，验证系统响应。
  • 优点： 模拟用户视角，发现功能性问题；无需访问代码。
  • 缺点： 无法验证程序内部逻辑；覆盖率有限。
• 白盒测试
  • 白盒测试是一种结构性测试，需要了解程序的内部逻辑和代码结构，测试人员通过分析代码设计测试用例。
    • 关注程序内部逻辑和实现细节。
    • 测试人员需要具备编程和代码分析能力。
    • 以代码覆盖率为目标，确保所有路径被测试。
  • 常用方法：
    • 语句覆盖： 测试代码中每个语句是否执行。
    • 分支覆盖： 测试代码中每个条件分支是否被执行。
    • 路径覆盖： 测试代码中所有可能的执行路径。
    • 循环测试： 测试循环结构的各种情况（如0次、1次、N次）。
  • 优缺点：
    • 优点： 能发现隐藏的逻辑错误；覆盖率高，保障代码质量。
    • 缺点： 不易发现功能性问题；测试成本较高。

路径测试（白盒测试）

实现方法：画程序流图 → 画DD路径图 → 根据覆盖指标设计测试 → 计算基本路径的个数/找出基本路径

DD路径

程序流图是一种有向图，其中节点表示语句，边表示控制流，具体转化方法如下：

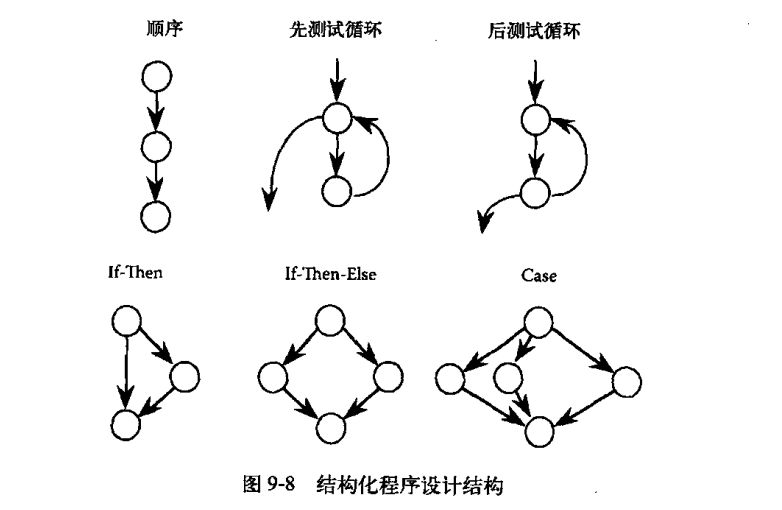
对于给定的程序，可以可以简化压缩为唯一的DD-路径图，使得：

• 情况1：由一个节点组成，入度=0
• 情况2：由一个节点组成，出度=0
• 情况3：由一个节点组成，入度 ≥ 2或出度 ≥ 2
• 情况4：由一个节点组成，入度=1并且出度=1
• 情况5：长度 ≥ 2的最大链(单入单出的最大序列：所有连续的单入单出的节点，合成一个单入单出的节点

DD-路径是程序中最小独立路径，不能被包括在其他DD-路径之中

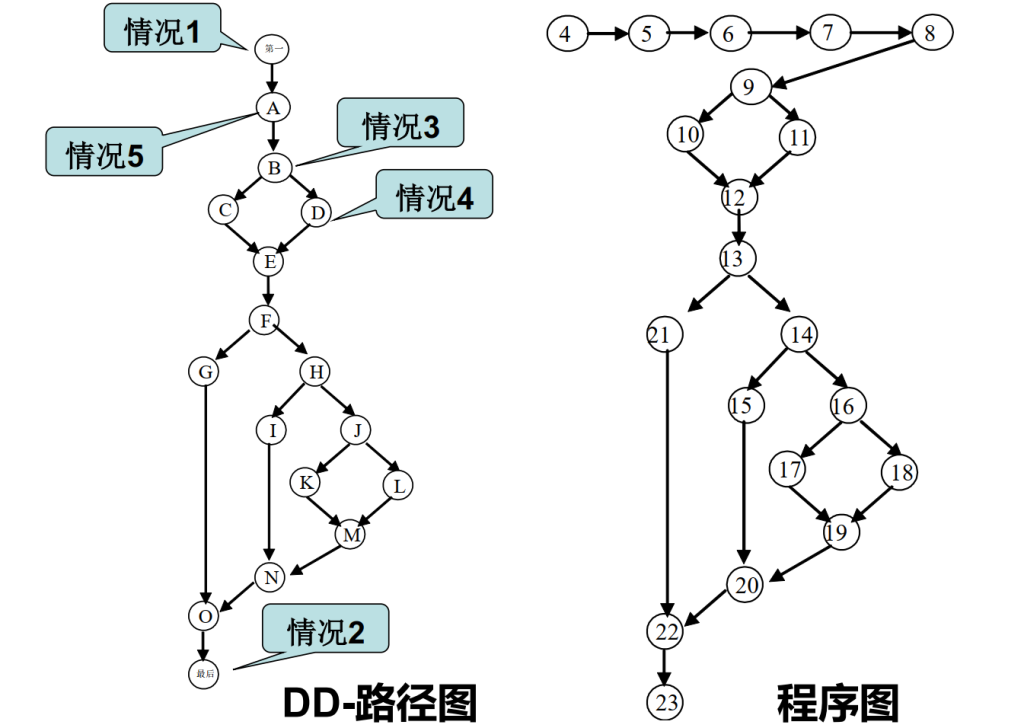
• 开始和结束作为单独的DD-路径
• While循环判断和IF条件判断作为单独的DD-路径（对应情况3，出度≥2）

测试覆盖指标/测试覆盖率

指标	描述
C0	所有语句（语句覆盖）
C1	所有DD-路径（分支/判断覆盖）
C1p	所有判断的每种分支（条件判断）
C2	C1覆盖+循环判断
Cd	C1覆盖+DD-路径的所有依赖对偶
Cmcc	多条件覆盖
Cik	包含最多K次循环的所有程序路径（通常K=2）
Cstart	路径具有“统计重要性”的部分
C∞	所有课能的执行路径

语句覆盖(C0)

使程序中每一可执行语句（每句话）至少执行一次

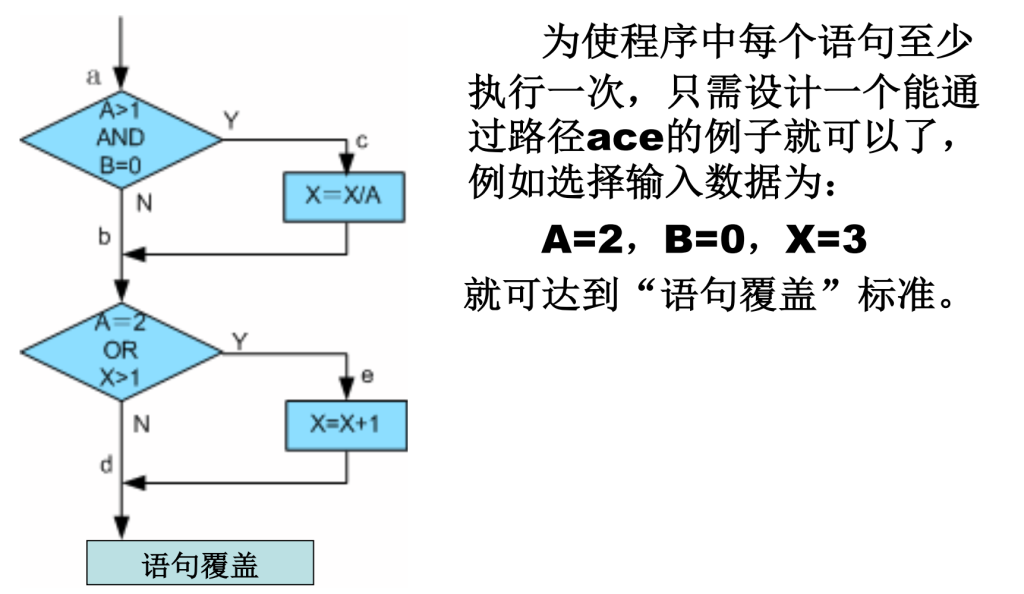
分支覆盖/判断覆盖（C1）[DD-路径测试]

使程序中的每个逻辑判断的取真取假分支至少经历一次；需要遍历DD路径图的每条边（而不仅仅是节 点）

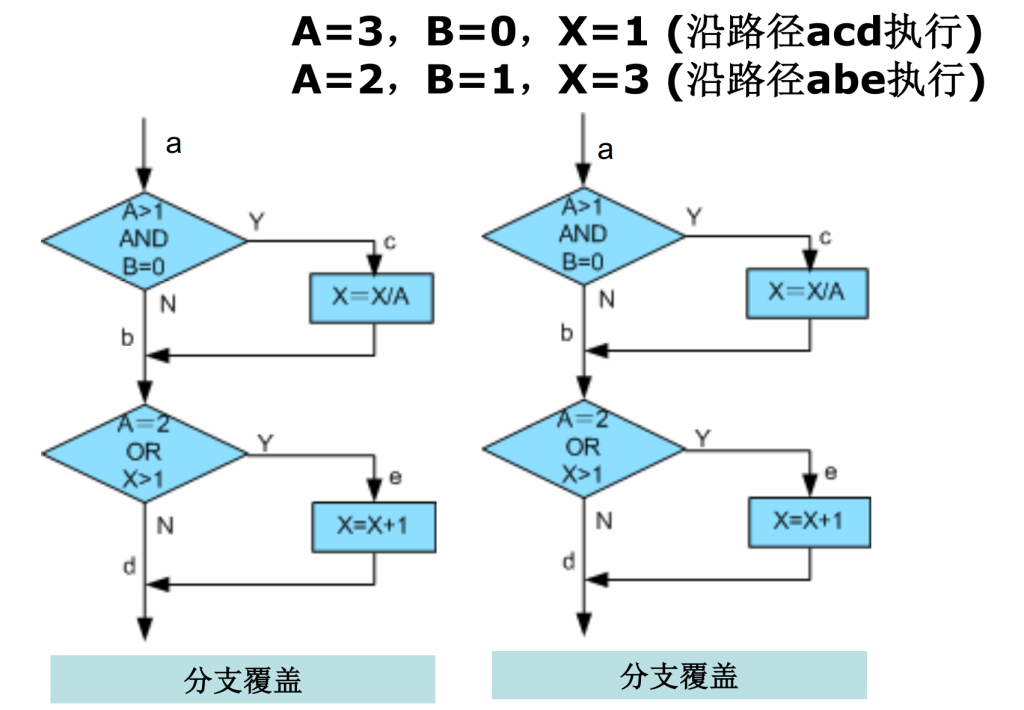
条件覆盖(C1p) [DD-路径测试]

所有判断中的每个子条件的可能取值（T/F）至少满足一次

距离在来说，在这个程序中有四个小条件，分别是 A > 1 , B = 0 , A = 2 , X > 1。
为了达到“条件覆盖”，则需要分别让这些条件满足和不满足一次，即：
在a点，要A > 1，A ≤ 1，B = 0，B ≠ 0 各出现一次
在b点，要A = 2，A ≠ 2，X > 1 ，X ≤ 1 各出现一次

最佳测试用例就是如下，这需要两个测试，上面所有条件都可以覆盖满足。

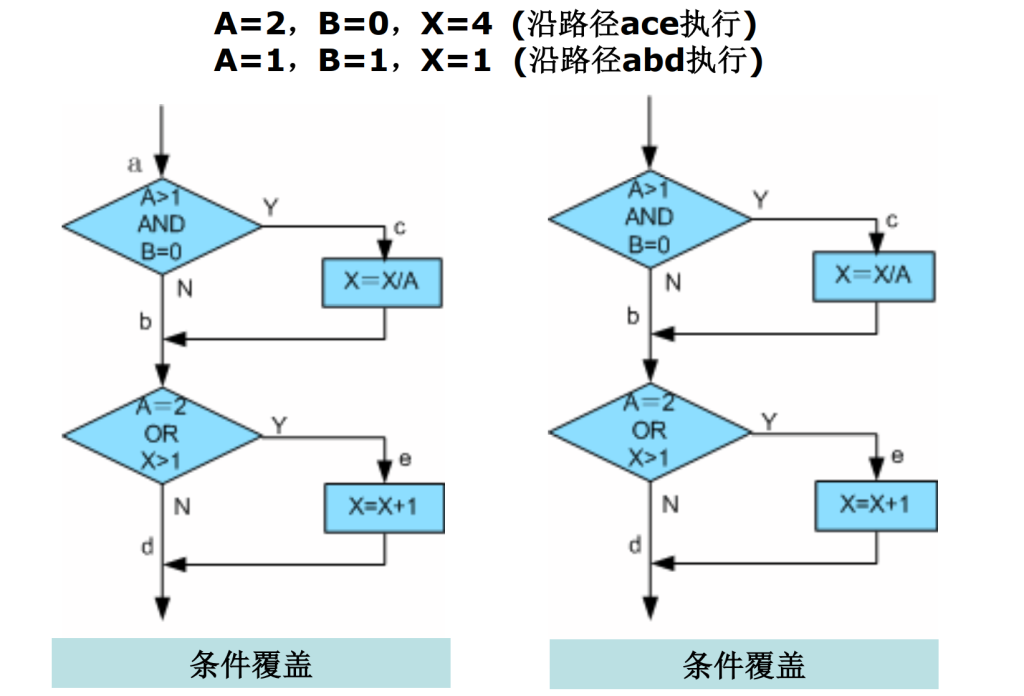
多条件覆盖（Cmcc）

每个判断式中，条件的各种可能组合都至少出现一次（条件组合覆盖）

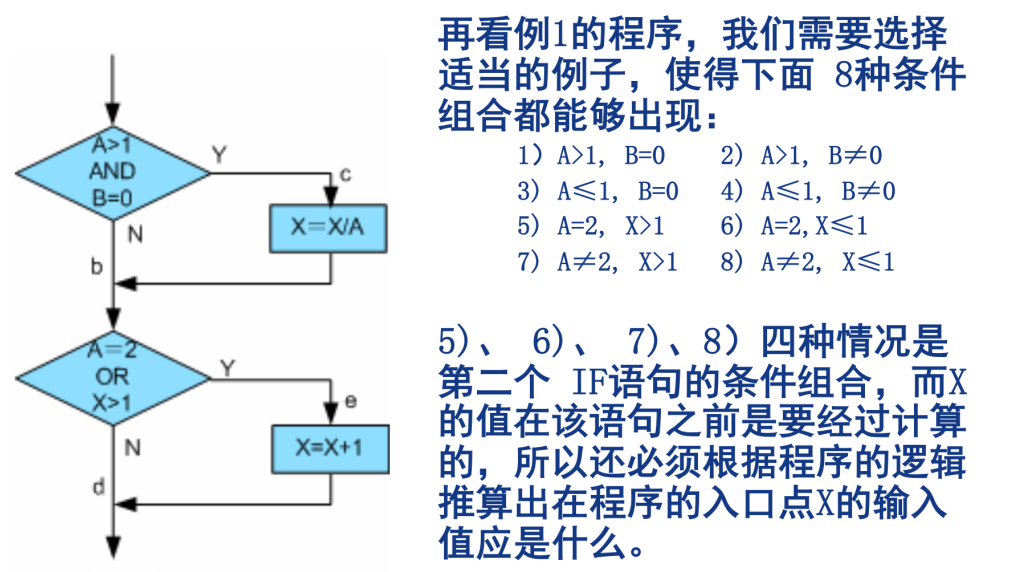
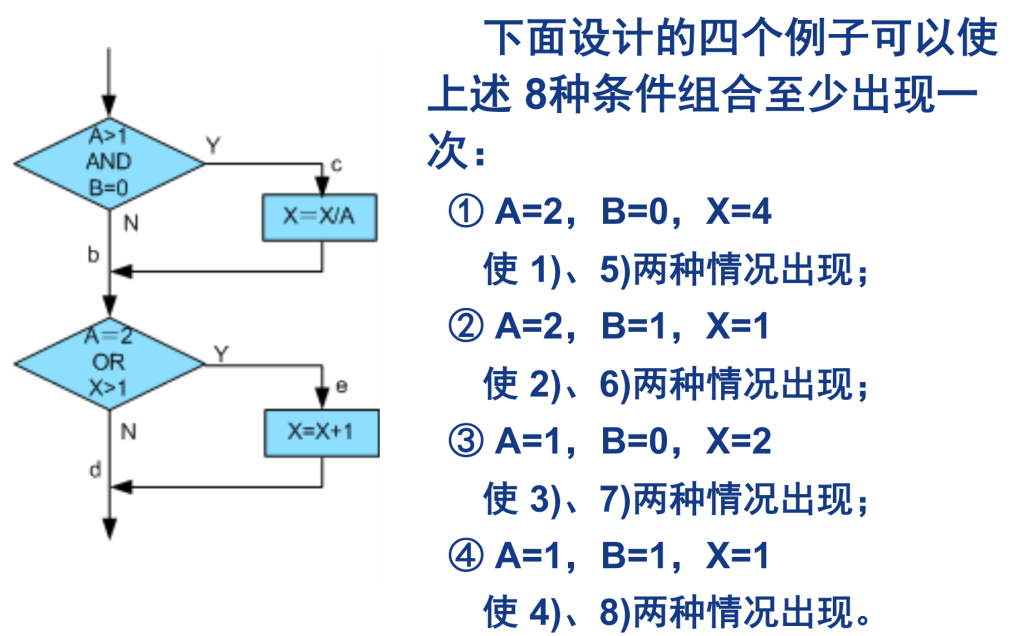
注意，多条件覆盖可能不能覆盖所有的路径，比如上述条件中acd就没有被执行。

分支/条件覆盖

既覆盖条件，又覆盖分支；既使每个条件可以取到不同的值，又使每个分支可以被取到。

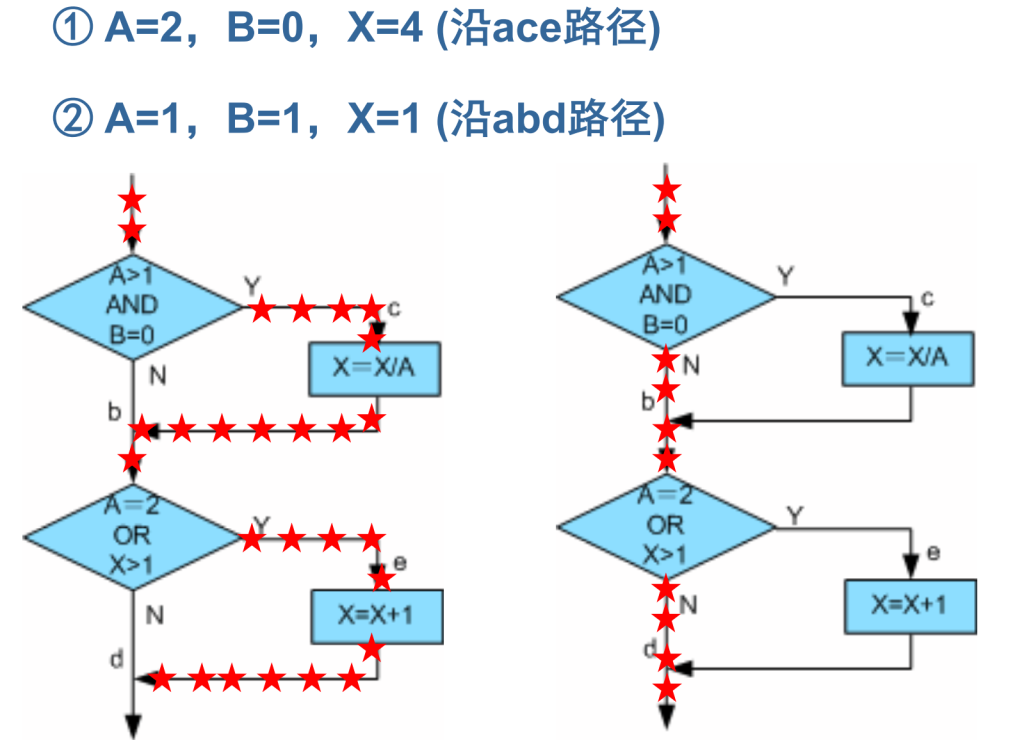
路径测试（C∞）

设计足够多的测试用例，覆盖被测试对象中的所有可能路径。

如上述例子中，需要覆盖 abd、abe、acd、ace（各种分支串联组合）

循环测试

思路：尽量转化成单循环来测试

• 单循环测试
  • 假设循环次数为N
    • a. 直接跳过循环
    • b. 循环次数为1
    • c. 循环次数为2
    • d. 循环次数为M，M<N
    • e. 循环次数为N-1，N，N+1
  • 嵌套循环测试
    • a. 先测试最内部循环，其它循环次数为1
    • b. 测试第二层循环，其它循环次数为1
    • c. 直到最外部循环完成测试
  • 级连循环测试
    • a. 分别采用单循环测试方法进行测试
  • 不规则循环测试
    • 无法测试——重新设计！

McCabe圈数（基（本）路径）

• 基(本)路径：程序图中相互独立的一组路径，使得该程序中的所有路径都可以用基路径线性表示；需要是完整路径，从起始节点到终止节点
• 圈复杂度：是一种为程序逻辑复杂性提供定量测度的软件度量，将该度量用于计算程序的基本的基本路径数目（圈复杂度是多少，基本路径就有几个）；圈复杂度可以衡量软件复杂度

基本路径必须从起始点到终止点的路径，包含一条其他基本路径不曾用到的边，或至少引入一个新处理语句或者新判断的程序通路；对于循环而言，基本路径应包含不执行循环和执行一次循环的路径

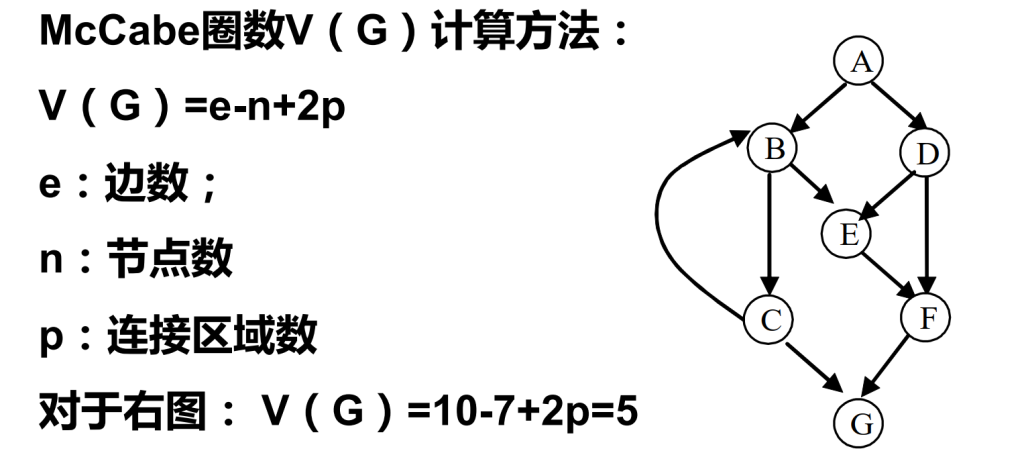
McCabe圈数： V(G) = e – n + 2p （不是强连通图（任意两点之间存在路径的图为连通图）；上图增加G连到A，就成为强连通图，公式变 为 V(G) = e – n + p ）

p：流程图中断开部分的数量（调用程序和子程序）

基本路径的选择——基线法

• 基本路径需要是完整路径，从起始节点到终止节点（A到G）
• 开始时先随意选一条
• 之后每次找下一条基本路径时，需要至少包含一个新的边/新的节点（对每个判断节点依次反转判断，保证每个节点都被反转判断即可）
• If 分支每个分支走到一遍，循环要包括一次循环和不循环两种

对于测试只用测基本路径即可，其他路径通可以通过基本路径线性组合表示。

数据流测试（白盒测试）

定义-使用（def-use）测试

• 定义节点（DEF(v, n））：
  • 节点 𝑛 是变量 𝑣 的定义节点，表示变量 𝑣 的值在节点 𝑛 被赋值或修改。
• 使用节点（USE(v, n））：
  • 节点 𝑛 是变量 𝑣 的使用节点，表示变量 𝑣 的值在节点 𝑛 被读取或操作。
• P-use（谓词使用）：
  • 在条件语句中使用变量（如 if 或 while 的条件）。
• C-use（计算使用）：
  • 在普通计算或操作中使用变量（如赋值右值或函数调用）。
• 定义-使用路径（du-path）：
  • 从定义节点 𝐷 𝐸 𝐹 ( 𝑣 , 𝑚 ) 到使用节点 𝑈 𝑆 𝐸 ( 𝑣 , 𝑛 ) 的路径，且路径中不包含其他对变量 𝑣 的定义节点。
• 定义-清除路径（dc-path）：
  • 从定义节点 𝐷 𝐸 𝐹 ( 𝑣 , 𝑚 )到使用节点 𝑈 𝑆 𝐸 ( 𝑣 , 𝑛 ) 的路径，且路径中没有任何其他对变量 𝑣 的重新定义。

程序图

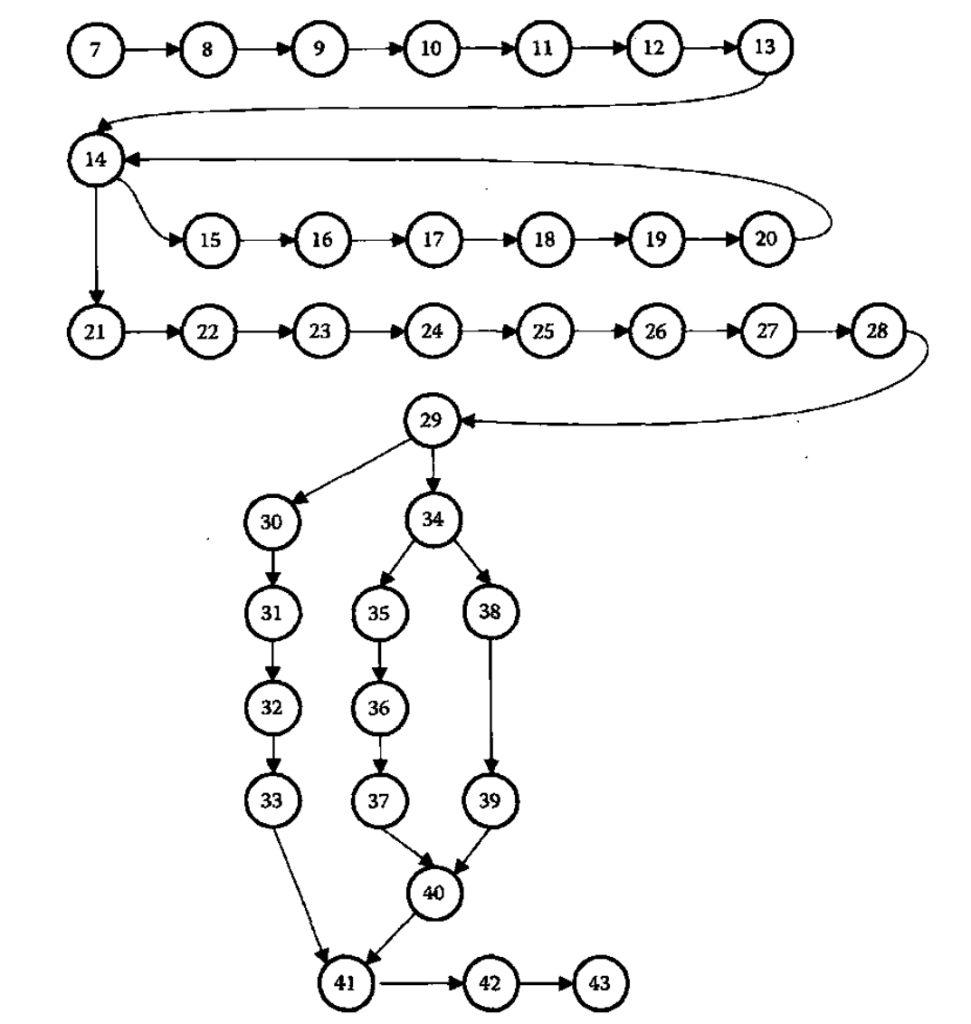
DD路径图（这里需要补充首尾节点）

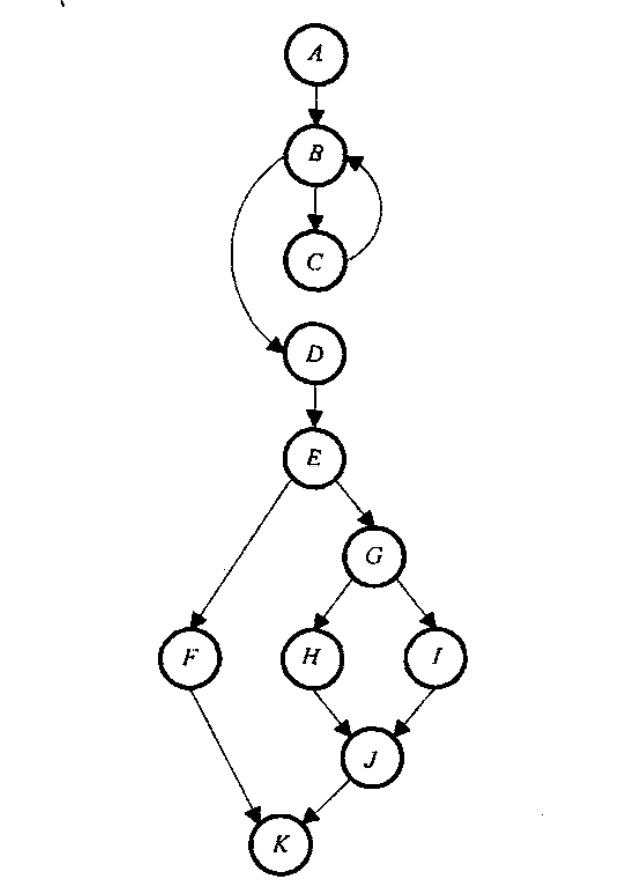
Def-Use表

定义使用路径

根据定义/使用表格遍历每个定义/使用对，注意while循环end while下一句是while判断
变量 locks ： DEF(locks,13) 、 DEF(locks,19) 、 USE(locks,14) 、 USE(locks,16)
产生的路径：

p1=<13,14> 
p2=<13,14,15,16>
p3=<19,20,14> 
p4=<19,20,14,15,16>

变量 totalLocks ：有2个定义节点， DEF(totalLocks,10) 和 DEF(totalLocks,16) ；3个使用节点， USE(totalLocks,16) 、 USE(totalLocks,21) 和 USE(totalLocks,24)

p1=<10,11,12,13,14,15,16> # 是定义清除的
p2=<10,11,12,13,14,15,16,17,18,19,20,14,21> # 因为节点16是可循环的，存在totalLocks再
定义现象，不是定义清除的
p3=<10,11,12,13,14,15,16,17,18,19,20,14,21,22,23,24>=<p2,22,23,24> # 不是定义清除的
p4=<16,16> # 不作为定义-使用路径
p5=<16,17,18,19,20,14,21> # 是定义清除的，有循环迭代问题
p6=<16,17,18,19,20,14,21,22,23,24> # 是定义清除的，有循环迭代问题

定义-使用路径测试覆盖指标

根据相应覆盖指标设计尽量少的测试用例，去覆盖对应指标包括的所有路径；每一个测试用例很可能覆盖很多定义-清除路径

• 全定义准则：每个定义节点到一个使用的定义清除路径。
• 全使用准则：每个定义节点到所有使用节点以及后续节点（后续所有分支，直到结束）的定义清除路径。
• 全谓词使用/部分计算使用准则：每个定义节点到所有谓词使用的定义清除路径，若无谓词使用，至少有一个计算使用的定义清除路径。
• 全计算使用/部分谓词使用准则：每个定义节点到所有计算使用的定义清除路径，若无计算使用，至少有一个谓词使用的定义清除路径。
• 全定义-使用路径准则：每个定义节点到所有使用节点以及后续节点的定义清除路径。包括有一次环路和或无环路的路径。

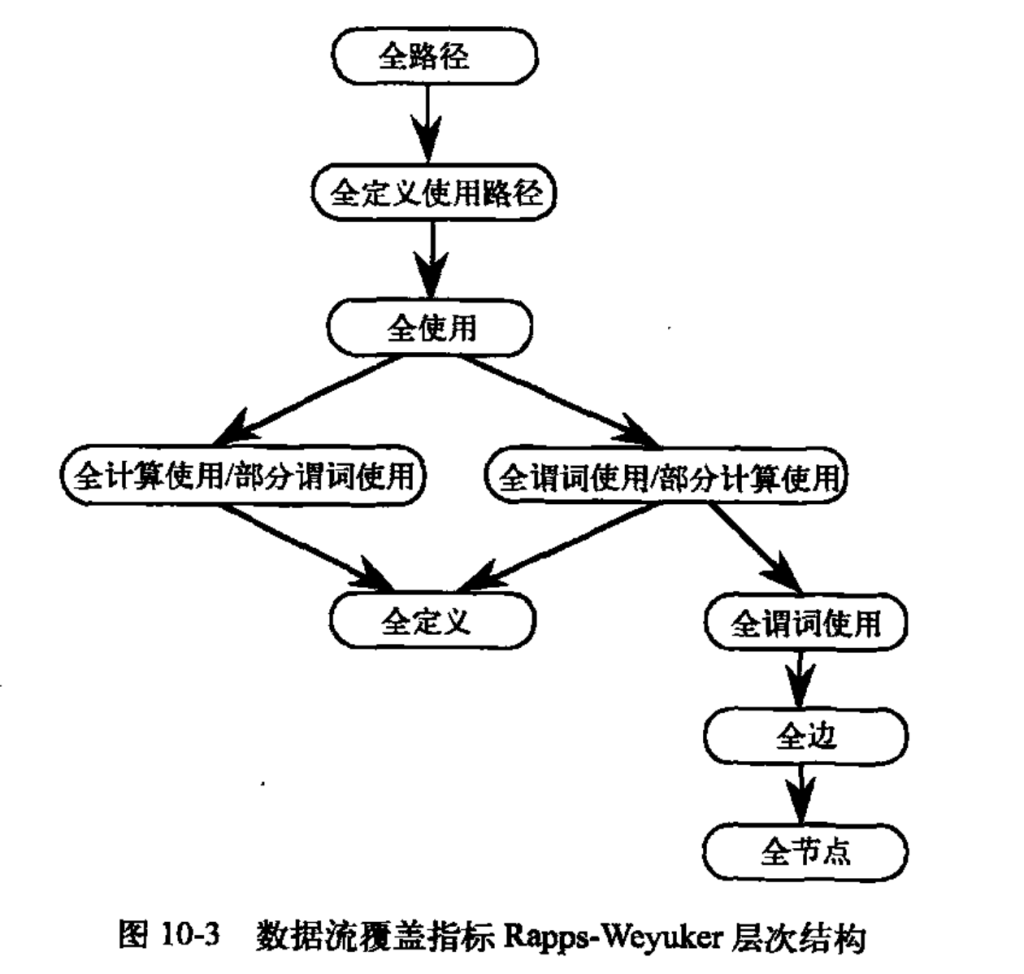
基于程序片的测试

本质：基于程序片的测试通过分析变量的依赖关系，确定变量的值如何受到程序的各个语句片段影响。核心思想是：如果某变量的定义和使用是正确的，并且所有依赖的变量的定义和使用也是正确的，那么整个程序可以被证明是正确的。

定义：程序片是一个程序中对某变量值产生直接或间接影响的所有语句的集合。它刻画了变量的定义和使用之间的依赖关系。

• USE（使用）的形式有：谓词使用、计算使用、输出使用、定位使用、迭代使用
• DEF（定义）的形式有：输入定义、赋值定义

作出贡献：会对变量本身的值产生影响（直接或间接）

1. 定义节点：
   程序片包括定义节点本身，和使用该变量的所有语句片的并集。
2. 使用节点：
   程序片包括上一个定义节点的程序片。如果存在分支条件或循环控制，则需包括相关的条件语句或循环控制语句。
3. 循环语句：
   如果变量在循环体中定义或使用，则程序片必须包括循环控制语句（如 while 和 end while），以及循环变量的相关语句片。
4. 条件判断：
   如果变量在条件分支中定义或使用，则程序片需包含条件判断所使用的变量的语句片。

第 i 个程序片 Si 表示为： Si:S(变量,语句n)={程序片包含的语句行号}

变量 Locks 有2个使用节点14、16，2个定义节点13、19，则：

• S1: S(Locks,13)={13} ：对于 13 行 Locks 变量可能造成影响的行，只有 13 行本身
• S2: S(Locks,14)={13,14,19,20} ：14 节点使用 Locks，前面 13 行定义 Locks 肯定有贡献；14 行变量决定是否进入 while 循环，如果进入那么循环体中 19 节点又会定义 Locks，从而对14行又产生影响，因此 14，19和20（决定循环体是否结束）都会对 14 节点的 Locks 产生影响
• S3: S(Locks,16)={13,14,19,20} ：16 节点的 Locks 显然不受到 16 节点的贡献，16 节点只是使用了 Locks 变量，但是不会对 Locks 的值产生影响
• S4: S(Locks,19)={13,14,19,20}

变量 stocks 和 barrels 要受循环变量 locks 的影响：

• S5:S(Stocks,15)={13,14,15,19,20} ：节点 15 语句对 stocks 变量赋值，自己本身会对 stocks变量做出贡献；并且 15 语句处于循环体内，因此决定是否进入该循环体的所有相关语句都应该属于这一程序片（13、14、19、20）
• S6:S(Stocks,17)={13,14,15,19,20}
• S7:S(Barrels,15)={13,14,15,19,20}
• S8:S(Barrels,18)={13,14,15,19,20}

totalApple: (def: 16,22; use: 22,27,30,35)
S (totalApple, 16) = {16}
S (totalApple, 22) = {16, 19, 20, 21, 22, 25, 26}
S (totalApple, 27) = {16, 19, 20, 21, 22, 25, 26}
S (totalApple, 30) = {16, 19, 20, 21, 22, 25, 26}
S (totalApple, 35) = {16, 19, 20, 21, 22, 25, 26}

只有16行的赋值和while循环对totalApple作出贡献。27，30，35是无贡献的use

回归测试

本质与目的：

回归测试是一种验证软件修改是否正确的方法，确保修改后的程序未损害已有功能，并验证修改是否达到预期效果。它的核心在于减少测试代价：不用运行所有测试用例，而是基于修改的部分选择相关测试用例，同时补充新的测试用例测试修改的功能。

回归测试策略：

1. 再测试全部用例（Test-all approach）：
   • 运行所有测试用例，确保完整性，但代价高。
2. 测试选择（Test Selection）：
   • 从原测试用例中选取一部分与修改相关的测试用例，达到验证目的。
   • 基于风险选择测试：
     • 优先运行重要、关键或可疑的测试用例，逐步降低风险。
   • 基于操作剖面选择测试：
     • 针对软件最重要或最频繁使用的功能优先选择测试用例。
   • 再测试修改的部分：
     • 将测试局限于被修改的模块及其接口，分析修改的影响。

步骤（从现有测试用例中选择一部分）

1. 识别出软件中被修改的部分
2. 从原基线测试用例库 T 中，排除所有不再适用的测试用例（对新版本不能运行的，废弃和冗余的），确定那些对新的软件版本依然有效的测试用例，其结果是建立一个新的基线测试用例库T0
3. 依据一定的策略从 T0 中选择测试用例测试被修改的软件
4. 如果必要，生成新的测试用例集 T1 ，用于测试 T0 无法充分测试的软件部分
5. 用 T1 执行修改后的软件

第(2)和第(3)步测试（核心），验证修改是否破坏了现有的功能，第(4)和第(5)步测试验证修改工作本身

回归测试用例选择方法

基于执行路径的测试选择（Execution Trace & Slice）：

对于以下程序

构造控制流图（CFG）：为程序 P 和修改后的程序 P′ 构造控制流图，表示程序中语句的执行路径。

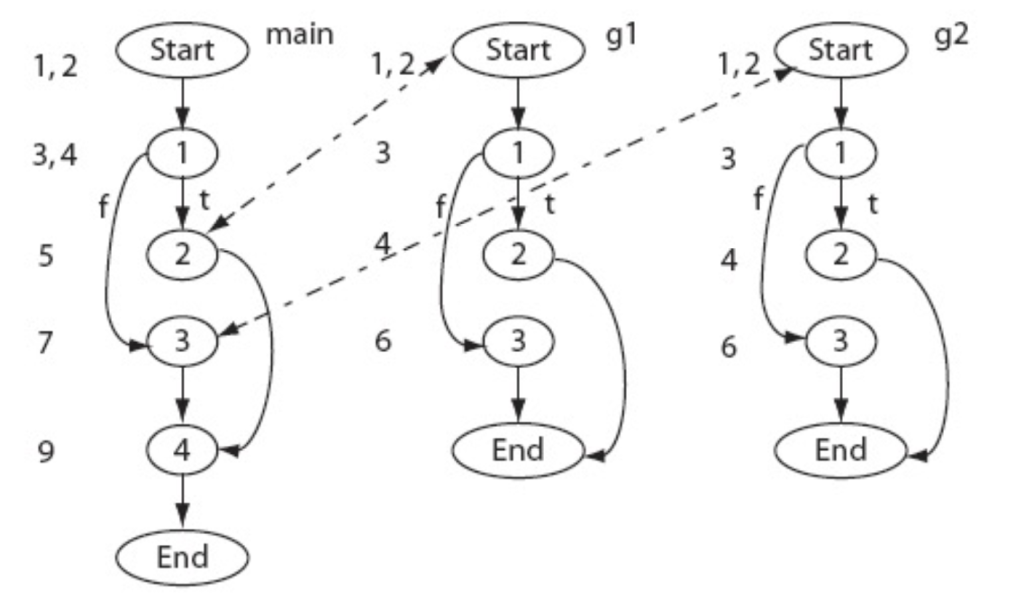
找到执行轨迹（Execution Trace）：对每个测试用例t，找到它在程序P 中的完整执行轨迹。

如 t1（x=1,y=3），从 main.Start 节点开始执行，到 main.1 节点，到第四行判断为 true，到 main.2 节点，调用 g1，到 g1.Start，……

构造测试向量（Test Vector）：对每个节点，记录经过该节点的测试用例。

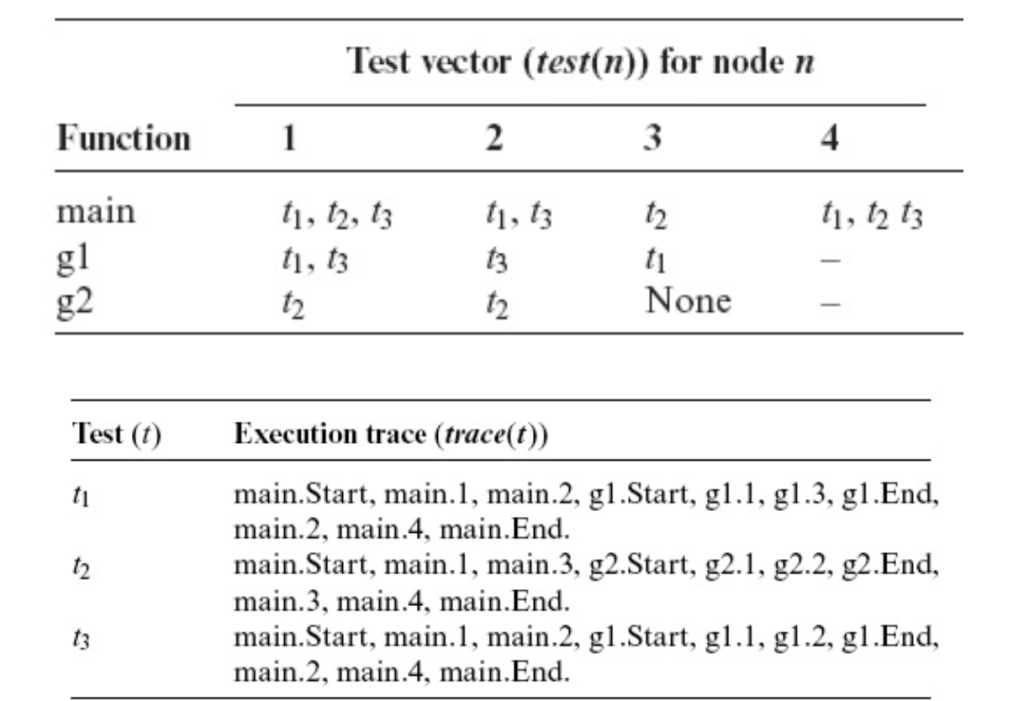
对于第一行，意思是例如main.1节点，经过了t1t2t3这三个测试，main.2节点，经过了t1,t3俩测试….

构造句法树（Syntax Tree）：分析程序 𝑃 和修改后的程序 𝑃 ′ ，判断节点是否在语义上发生了变化。

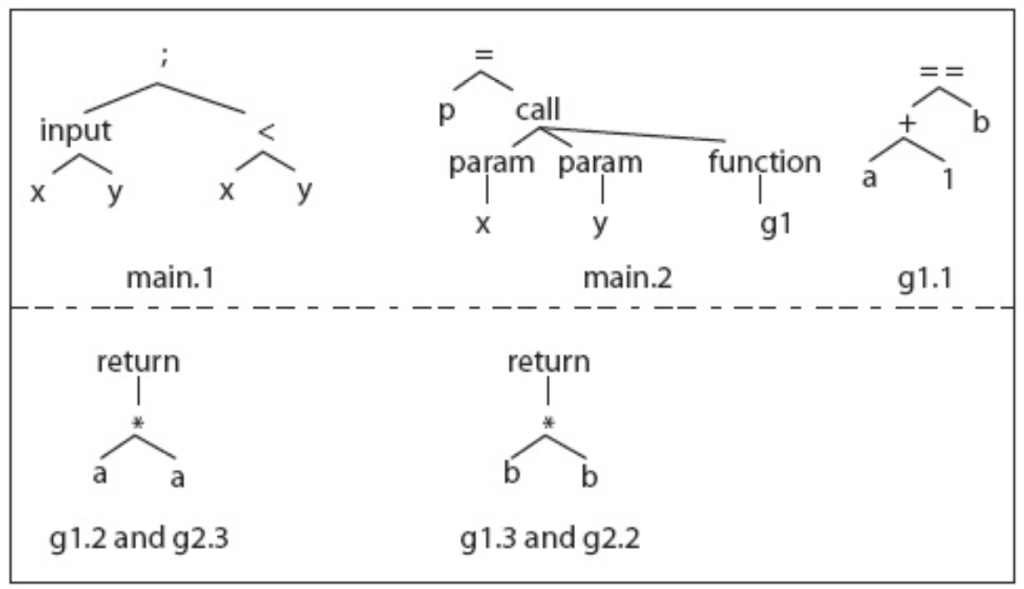
选择测试用例（Test Selection）：只测试修改过的地方对应的测试用例

选择测试用例（Test Selection）：只选择经过修改的节点的测试用例。例如：如果函数 𝑔 1的节点 𝑔 1.1 被修改，则应选择 𝑇 ′ = { 𝑡 1 , 𝑡 3 } 进行测试。

基于测试最小化的选择（Test Minimization）：

选择最少的测试用例，覆盖所有被修改的代码实体。

2. 基于测试最小化的选择（Test Minimization）：

选择最少的测试用例，覆盖所有被修改的代码实体。

步骤：

1. 定义可测实体单位：
   • 如函数、语句、基本块、定义/使用路径等，找出所有可测实体。
2. 分析测试用例覆盖：
   • 确定每个测试用例是否执行了哪些可测实体。例如：
     • 测试用例 t1 执行 main，但不执行f。
     • 测试用例 t2 执行 main 和 f。
3. 选择最少的测试用例：
   • 选取最少的测试用例，使其能够覆盖所有被修改的可测实体。
   • 例如：如果修改涉及函数 main 和 f，则选择t2 即可覆盖所有修改。

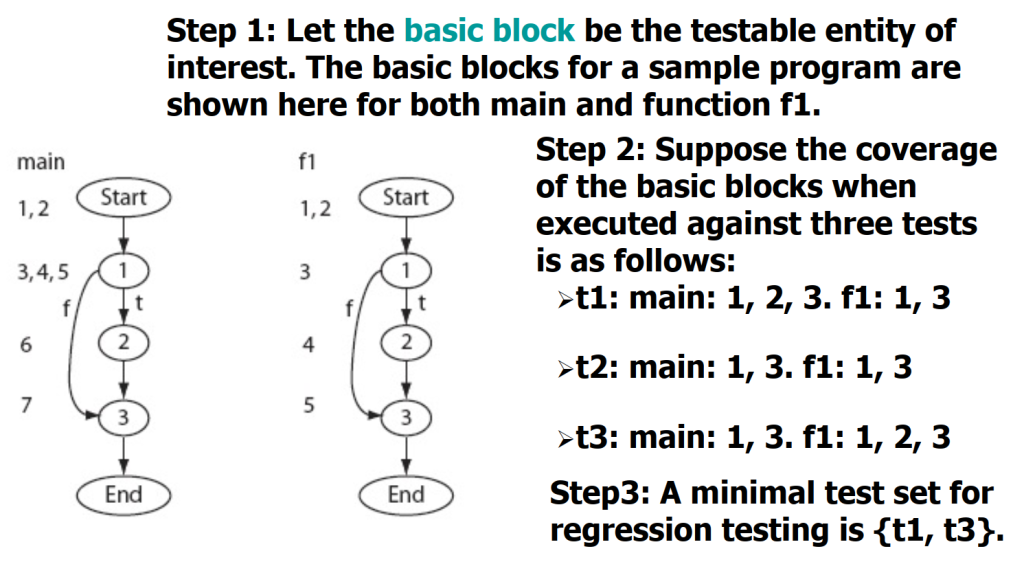
案例：

• 如果程序包含函数 𝑚𝑎𝑖𝑛 和 𝑓，测试用例 𝑡1 测试 𝑚𝑎𝑖𝑛，而 𝑡2测试 𝑚𝑎𝑖𝑛和 𝑓。
• 修改涉及 𝑓，则选择测试用例 𝑡2 进行回归测试，最小化测试成本。

如上述需要在基本块全部覆盖的前提下，选最少的测试用例

基于测试优先级的选择（Test Prioritization）：

给测试评估优先级，根据测试优先级来选择（先测高优先级），如按照测试用例经过的实体数量，定优先级（经过多的，优先级高），选的数量可以自由综合考虑

变异测试

测试是否充分是软件测试中的重要问题。变异测试是一种评估测试充分性的技术，通过对程序进行小修改（模拟程序员可能犯的错误），验证现有测试用例是否能够发现这些错误，从而增强测试的充分性。

如何说明测试充分？覆盖率和变异测试

通过程序的变异（改程序本身），看修改后的程序能否通过原本的测试（模拟程序员犯的错误，把原本的程序改错，某一些用例就无法通过了）

1. 变异体 (Mutant)：
   变异体是通过对原程序 P 进行小修改生成的程序 P′。这些修改模拟可能的编程错误。
2. 测试充分性验证：
   • 等价变异体： 如果变异体 P′ 和原程序 P 在语义上完全等价（任何测试用例都无法区分它们），说明测试用例没问题。
   • 非等价变异体： 如果变异体 P′ 和原程序 P 不等价，但测试用例无法区分它们，说明测试用例不充分，需要补充新的测试用例。
3. 变异体的状态：
   • 被杀死的变异体 (Killed Mutant)： 测试用例能够区分变异体和源程序，变异体被杀死。
   • 存活的变异体 (Live Mutant)： 测试用例无法区分变异体和源程序，变异体存活。
4. 充分测试的目标：
   如果所有非等价变异体都被杀死，说明测试是充分的。

具体步骤：

1. 生成变异体：

通过对源程序进行小修改生成变异体，模拟可能的编程错误。

• 值变异： 修改变量的值（如循环计数变量增加或减少 1）。
  例：将变量起始值 x 改为 x+1 或 x−1。
• 语句变异： 删除、重复或颠倒代码块中的语句。
  例：删除某个赋值语句或交换两个代码块的顺序。
• 运算符变异： 修改代码中的运算符。
  例：将 > 替换为 <，或将 + 替换为 −。
• 常见变异操作：

变异操作	原代码	变异体代码
变量替换	z=x∗y+1	z=x∗x+1
关系符替换	if(x<y)	if(x>y)
Off-by-1	z=x∗y+1	z=(x+1)∗y+1
替换为 0	z=x∗y+1	z=0∗y+1
运算符替换	z=x∗y+1	z=x+y+1

• N 阶变异体：
  • 修改源程序的 N 个地方。
  • 一般只生成一阶变异体（修改一个地方）即可。

 执行测试用例：

在每个变异体上运行测试用例，比较结果是否与原程序一致。

• 如果测试用例结果与原程序不一致，说明变异体被杀死。
• 如果测试用例结果与原程序一致，说明变异体存活。

判断等价变异体：

分析存活变异体是否与源程序语义等价。

• 等价变异体： 测试用例无法区分，说明测试用例没问题。
• 非等价变异体： 测试用例无法区分，说明测试用例不充分。

增强测试用例：

如果存在非等价变异体，需要生成新的测试用例，使变异体能够被区分。

• 尽量增加最少的测试用例，确保所有非等价变异体都被杀死。

评价指标：

mutation score（MS）： MS = 被杀死变异体数量/(变异体总个数-等价变异体数量)

=1充分，<1越大越充分，需要补充新的测试用例

案例分析：

源程序：

实现两个数的求和：

cint foo(int x, int y) {
    return (x - y); // 应该是 x + y
}

测试用例集 𝑇T：

• 𝑡1:⟨𝑥=1,𝑦=0⟩
• 𝑡2:⟨𝑥=−1,𝑦=0⟩

生成变异体：

1. 𝑀1:将 𝑥−𝑦改为 𝑥+𝑦。
2. 𝑀2:将 𝑥−𝑦 改为 𝑥−0。
3. 𝑀3:将 𝑥−𝑦改为 0+𝑦。

测试结果：

测试用例	原程序 foo(t)	变异体 M1(t)	变异体 M2(t)	变异体 M3(t)
𝑡1	1	1	1	0
𝑡2	−1	−1	−1	0
		live	live	killed

• 𝑀1：存活（测试用例无法区分）。
• 𝑀2：存活（测试用例无法区分）。
• 𝑀3：被杀死。

增强测试：

1. M1：需要区分 x−y 和 x+y，即 𝑦≠0。
   • 新增测试用例 𝑡3:⟨𝑥=1,𝑦=1⟩。
2. M2：需要区分 x−y 和 𝑥−0，即 𝑦≠0。
   • 新增测试用例 𝑡3 同样有效。

适用场合：
程序非常重要，安全等级高（如航空、医疗、金融领域）。
普通程序通常不需要如此严格的测试充分性。