数据集筛选 – 涼宮ハルヒ

tinyBenchmarks: evaluating LLMs with fewer examples

纯数学方法，聚类

三步走：

IRT 参数化：首先利用历史数据，通过 IRT 模型学习全量数据集中每个问题的潜在参数（主要是区分度 $\alpha$ 和难度 $\beta$）。
聚类抽样：将这些参数作为每个问题的特征向量进行聚类（Clustering）。
选出代表：这样选出的 100 个例子能最大限度地覆盖不同难度和区分度的题目，避免了随机抽样的偏差。

IRT如何估算呢？

部分 A：观测分（低偏差，高方差） 直接计算模型在那 100 个“锚点”问题上的加权平均分。这反映了当下的真实表现，但样本少导致波动大。
部分 B：预测分（低方差，潜在偏差） 利用 IRT 模型。根据模型对这 100 题的回答，反向推断出该模型的**“潜在能力值” ($\theta$)。然后把这个能力值代入 IRT 公式，去预测**该模型在剩余所有未测试题目上的得分概率。
混合 (IRT++) 最终得分 = $\lambda \times$ 观测分 + $(1-\lambda) \times$ 预测分。
- $\lambda$ 是一个通过统计学方法计算出的权重，用于在方差和偏差之间取得最佳平衡。
Open LLM Leaderboard (大规模数据)
- 总模型数：约 400 个 (具体为 395 个 + 40 个特定微调模型)。
- 训练集 (Train)：约 300+ 个（较旧的模型）。
- 测试集 (Test)：约 40-80 个（最新发布的模型）。
- 注：这是数据最丰富的一组，验证效果也最强。
HELM (小规模数据)
- 总模型数：仅 37 个。
- 训练集：约 19-28 个（50% – 75%）。
- 测试集：约 9-18 个。
MMLU / AlpacaEval
- 大致都在 100-300 个模型这个量级。

数据规模

作者认为100左右就比较好了，可以达到2%以内的误差控制

基准测试 (Benchmark)	原始题量 (Original)	缩减后题量 (Tiny)	压缩比例	备注
MMLU	14,042	100	0.7%	压缩了140倍
Open LLM LB	~29,000	600	2%	含6个任务，每个任务留100题
HELM	~5,000	100	2%	每个场景(Scenario)留100题
AlpacaEval 2.0	805	100	12%	这是一个比较小的基准

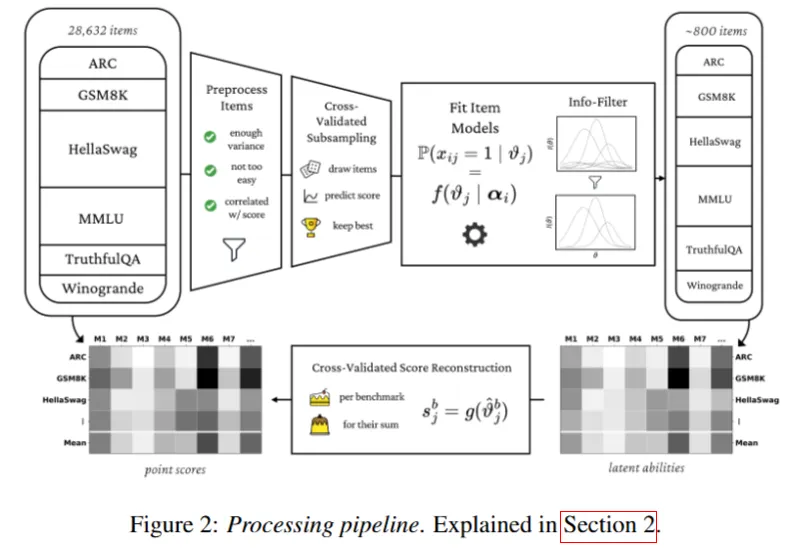
1.数据预处理

去掉太简单太难的，方差过高的题目。计算部分-整体相关性 (Point-biserial correlation)：剔除那些与总分相关性极低甚至负相关的题目（即答对该题的模型反而总分较低的异常题）。

2.心理测量学建模：项目反应理论 (Item Response Theory, IRT)

假设： 每个模型有一个潜在能力值 $（\theta，scalar ability）$，每个题目有其特性参数（如难度 $\delta$ 和区分度 $a$）。
模型： 作者使用了 2PL、3PL 和 4PL（参数逻辑斯蒂）模型来拟合数据。
- 例如 2PL 模型公式：$P(\text{correct}) = \sigma(a_i \theta_j – \delta_i)$。这意味着模型答对题目的概率取决于其能力值与题目难度的关系，以及题目的区分度。

3.信息过滤 (Information Filtering)

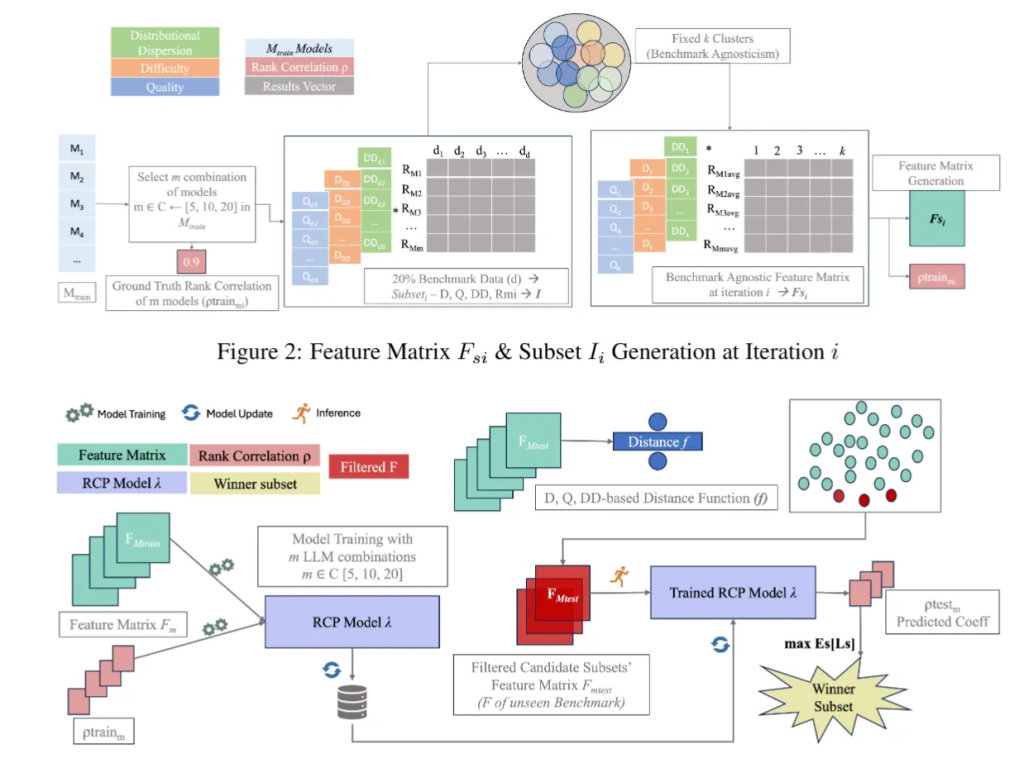
特征提取 -> 模型热身 -> 预测训练 -> 验证对比

1.步骤1，初筛，筛选掉选择高度重复的样本。利用embadding相似度（语义）和排名相关性（效果），超过一定阈值的话剔除，只保留一个

2.步骤2，使用遗传算法，选出特定的自己预测在样本上的得分，误差越小越好 • 目的： 从过滤后的数据中搜索出最佳组合。

将“挑选子集”建模为优化问题。使用遗传算法 (Genetic Algorithm) 进行迭代搜索，目标函数是最小化“子集得分”与“全集得分”之间的预测误差 (RMSE)。
1. 随机生成多个子集（种群）。
2. 评估每个子集的预测能力。
3. 通过锦标赛选择、交叉 (Crossover)、变异 (Mutation) 生成新一代子集。
4. 不断迭代，直到找到表现最好的子集。

3.步骤3：基于归因的样本精选

目的： 解决单纯遗传算法可能陷入局部最优的问题，提高搜索效率。
手段： 计算每个样本对预测总分的贡献度 (Attribution)。将样本分为“高贡献”、“低贡献”和“随机”三组，在这些组内再次运行遗传算法进行精细化搜索，最终选出既具代表性又具多样性的测试集。